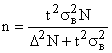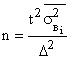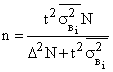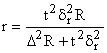- Общая характеристика выборочного наблюдения.
- Ошибки выборки.
- Распространение выборочных результатов на генеральную совокупность.
- Определение необходимого объема выборки.
1. Общая характеристика выборочного наблюдения
Статистическое наблюдение можно организовать сплошное и несплошное. Сплошное наблюдение предусматривает обследование всех единиц изучаемой совокупности, что связано с большими трудовыми и материальными затратами. Изучение не всех, а лишь некоторой части единиц совокупности, по которой можно судить о свойствах всей совокупности в целом, осуществляется несплошным наблюдением. Самым распространенным является выборочное наблюдение, при котором отбор подлежащих исследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность. Наблюдение организуется таким образом, что эта часть отобранных единиц в уменьшенном масштабе репрезентирует, т.е. представляет всю совокупность.
Вся совокупность единиц, из которой производится отбор, называется генеральной, ее обобщающие показатели – генеральными. Единицы, отобранные для непосредственного наблюдения, представляют собой выборочную совокупность, или просто выборку.
Основные характеристики параметров генеральной и выборочной совокупностей обозначаются следующими символами:
N – |
объем генеральной совокупности; |
n – |
объем выборки; |
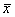 – – |
генеральная средняя, т.е. среднее значение признака в генеральной совокупности; |
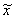 – – |
выборочная средняя; |
p – |
генеральная доля (доля единиц, обладающих изучаемым признаком, в общем числе единиц генеральной совокупности; |
w – |
выборочная доля; |
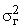 – –
|
генеральная дисперсия (дисперсия признака в генеральной совокупности); |
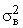 – –
|
выборочная дисперсия того же признака; |
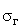 – –
|
среднее квадратическое отклонение в генеральной совокупности; |
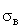 – –
|
среднее квадратическое отклонение в выборочной совокупности |
Преимущества выборочного наблюдения:
- экономия времени и средств (в результате сокращения объема работ);
- сведение к минимуму порчи или уничтожения исследуемых объектов (определение прочности пряжи при разрыве, испытания электрических лампочек на продолжительность горения, проверка консервов на доброкачественность);
- высокая точность результатов обследования благодаря сокращению ошибок, происходящих при регистрации.
Эти преимущества можно реализовать, если наблюдение организовано и проведено в соответствии с научными принципами теории выборочного метода, обеспечивающими репрезентативность полученной выборки. Такими принципами являются:
- обеспечение случайности отбора, т.е. каждая единица совокупности должна иметь равную возможность попасть в выборку;
- достаточное число выборки.
Количество отобранных в выборку единиц обычно определяется исходя из принятого процента выборки КВ:
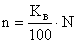
Так при 5 %-ной выборке из партии деталей в 1000 ед. объем выборки составляет 50 ед, а при 10 %-ной выборку – 100 ед.
(При выборочном наблюдении обычно используют два основных вида обобщающих показателей: среднюю количественного признака и относительную величину альтернативного признака – долю (удельный вес).
Выборочная доля w, или частость, определяется отношением:
 ,
,
где m – число единиц, обладающих изучаемым признаком).
Основная задача выборочного наблюдения состоит в том, чтобы на основе характеристик выборочной совокупности (например, средней) получить достоверные суждения об аналогичных показателях (средней) в генеральной совокупности. При этом следует иметь в виду, что при статистических исследованиях возникают ошибки двух видов: регистрации и репрезентативности.
Ошибки регистрации могут иметь случайный и систематический (тенденциозный) характер. Случайные ошибки обычно уравновешивают друг друга, так как не имеют преимущественного направления в сторону увеличения или уменьшения значения изучаемого признака. Систематические ошибки направлены в одну сторону и возникают в связи с принятым способом отбора или нарушением его правил. Их можно избежать при правильной организации и проведении наблюдения.
Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождения между величинами выборочных и соответствующих генеральных показателей. Избежать ошибок репрезентативности нельзя, но, пользуясь методами теории вероятности, можно свести к минимальным значениям. Значение ошибки репрезентативности зависит от вида, метода и способа формирования выборочной совокупности.
По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборку отбирают отдельные единицы генеральной совокупности, при групповом – качественно однородные группы или серии единиц. Комбинированный отбор – это сочетание 1-го и 2-го видов.
По методу отбора различают повторную и бесповторную выборку. При повторном отборе попавшая в выборку единица после регистрации возвращается в генеральную совокупность и участвует в дальнейшем отборе. Таким образом, объем генеральной совокупности не меняется. На практике такой метод отбора встречается редко.
При бесповторной выборке единица, попавшая в выборочную совокупность, в генеральную не возвращается, т.е. объем генеральной совокупности в процессе исследования сокращается.
Способ отбора определяет конкретный механизм или процедуру отбора единиц из генеральной совокупности. Наиболее распространены следующие выборки: собственно-случайная, механическая, типическая (или расслоенная, районированная), серийная, комбинированная.
По степени обхвата единиц совокупности различают большие и малые (n<30) выборки.
2. Ошибки выборки
Рассмотрим подробно перечисленные выше способы формирования выборочной совокупности и возникающие при этом ошибки репрезентативности.
Собственно-случайная выборка основывается на отборе единиц из генеральной совокупности наугад без каких-либо элементов системности. Технически собственно-случайный отбор проводят методом жеребьевки (например, розыгрыши лотерей) или по таблице случайных чисел.
Собственно-случайный отбор «в чистом виде» в практике выборочного наблюдения применяется редко, но он является исходным среди других видов отбора, в нем реализуются основные принципы выборочного наблюдения. Рассмотрим некоторые вопросы теории выборочного метода и формулы ошибок для простой случайной выборки.
Ошибка выборочного наблюдения – это разность между величиной параметра в генеральной совокупности, и его величиной, вычисленной по результатам выборочного наблюдения. Для средней количественного признака ошибка выборки определяется
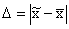
Показатель  называется предельной ошибкой выборки.
называется предельной ошибкой выборки.
Выборочная средняя 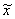 является случайной величиной, которая может принимать различные значения в зависимости от того, какие единицы попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки
является случайной величиной, которая может принимать различные значения в зависимости от того, какие единицы попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки 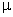 , которая зависит от:
, которая зависит от:
- объема выборки: чем больше численность, тем меньше величина средней ошибки;
- степени изменения изучаемого признака: чем меньше вариация признака, а, следовательно, и дисперсия, тем меньше средняя ошибка выборки.
При случайном повторном отборе средняя ошибка рассчитывается
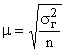 .
.
Практически генеральная дисперсия точно не известна, но в теории вероятности  доказано, что
доказано, что
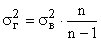 .
.
Так как величина 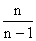 при достаточно больших n близка к 1, можно считать, что
при достаточно больших n близка к 1, можно считать, что 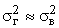 . Тогда средняя ошибка выборки может быть рассчитана:
. Тогда средняя ошибка выборки может быть рассчитана:
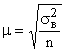 .
.
Но в случаях малой выборки (при n<30) коэффициент 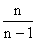 необходимо учитывать, и среднюю ошибку малой выборки рассчитывать по формуле
необходимо учитывать, и среднюю ошибку малой выборки рассчитывать по формуле
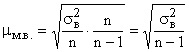 .
.
При случайной бесповторной выборке приведенные формулы корректируются на величину 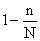 . Тогда средняя ошибка бесповторной выборки:
. Тогда средняя ошибка бесповторной выборки:
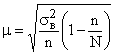 и
и 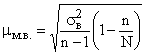 .
.
Т.к. 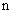 всегда меньше
всегда меньше 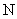 , то множитель (
, то множитель (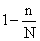 ) всегда меньше 1. Это значит, что средняя ошибка при бесповторном отборе всегда меньше, чем при повторном.
) всегда меньше 1. Это значит, что средняя ошибка при бесповторном отборе всегда меньше, чем при повторном.
Механическая выборка применяется, когда генеральная совокупность каким-либо способом упорядочена (например, списки избирателей по алфавиту, телефонные номера, номера домов, квартир). Отбор единиц осуществляется через определенный интервал, который равен обратному значению процента выборки. Так при 2% выборке отбирается каждая 50 единица =1/0,02 , при 5% каждая 1/0,05=20 единица генеральной совокупности.
Начало отсчета выбирается разными способами: случайным образом, из середины интервала, со сменой начала отсчета. Главное при этом – избежать систематической ошибки. Например, при 5% выборке, если первой единицей выбрана 13-я, то следующие 33, 53, 73 и т.д.
По точности механический отбор близок к собственно-случайной выборке. Поэтому для определения средней ошибки механической выборки используют формулы собственно-случайного отбора.
При типическом отборе обследуемая совокупность предварительно разбивается на однородные, однотипные группы. Например, при обследовании предприятий это могут быть отрасли, подотрасли, при изучении населения – районы, социальные или возрастные группы. Затем осуществляется независимый выбор из каждой группы механическим или собственно-случайным способом.
Типическая выборка дает более точные результаты по сравнению с другими способами. Типизация генеральной совокупности обеспечивает представительство в выборке каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. Следовательно, при нахождении ошибки типической выборки согласно правилу сложения дисперсий (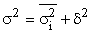 ) необходимо учесть лишь среднюю из групповых дисперсий. Тогда средняя ошибка выборки:
) необходимо учесть лишь среднюю из групповых дисперсий. Тогда средняя ошибка выборки:
при повторном отборе
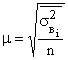 ,
,
при бесповторном отборе
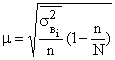 ,
,
где  – средняя из внутригрупповых дисперсий в выборке.
– средняя из внутригрупповых дисперсий в выборке.
Серийный (или гнездовой) отбор применяется в случае, когда генеральная совокупность разбита на серии или группы до начала выборочного обследования. Этими сериями могут быть упаковки готовой продукции, студенческие группы, бригады. Серии для обследования выбираются механическим или собственно-случайным способом, а внутри серии производится сплошное обследование единиц. Поэтому средняя ошибка выборки зависит только от межгрупповой (межсерийной) дисперсии, которая вычисляется по формуле:
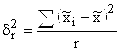
где r – число отобранных серий;
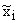 – средняя і-той серии.
– средняя і-той серии.
Средняя ошибка серийной выборки рассчитывается:
при повторном отборе
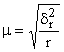 ,
,
при бесповторном отборе
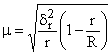 ,
,
где R – общее число серий.
Комбинированный отбор представляет собой сочетание рассмотренных способов отбора.
Средняя ошибка выборки при любом способе отбора зависит главным образом от абсолютной численности выборки и в меньшей степени – от процента выборки. Предположим, что проводится 225 наблюдений в первом случае из генеральной совокупности в 4500 единиц и во втором – в 225000 единиц. Дисперсии в обоих случаях равны 25. Тогда в первом случае при 5 %-ном отборе ошибка выборки составит:
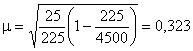
Во втором случае при 0,1 %-ном отборе она будет равна:
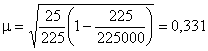
Таким образом, при уменьшении процента выборки в 50 раз, ошибка выборки увеличилась незначительно, так как численность выборки не изменилась.
Предположим, что численность выборки увеличили до 625 наблюдений. В этом случае ошибка выборки равна:
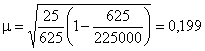
Увеличение выборки в 2,8 раза при одной и той же численности генеральной совокупности снижает размеры ошибки выборки более чем в 1,6 раза.
3. Распространение выборочных результатов на генеральную совокупность
Конечной целью выборочного наблюдения является характеристика генеральной совокупности. Учитывая, что на основе выборочного обследования нельзя дать точное значение изучаемого параметра генеральной совокупности, определяют пределы, в которых он находится.
Возможные отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности показывает средняя ошибка выборки. Если, например средняя продолжительность горения лампочки по выборке составила 300 час, а ошибка выборки 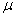 =10 час, то среднюю продолжительность горения всей партии лампочек, из которой взята выборка, можно ожидать в пределах 300
=10 час, то среднюю продолжительность горения всей партии лампочек, из которой взята выборка, можно ожидать в пределах 300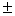 10 час, т.е. от 290 до 310 ч.
10 час, т.е. от 290 до 310 ч.
Однако то, что генеральная средняя не выйдет за данные пределы, можно утверждать лишь с определенной степенью вероятности Р.
Доказано, что утверждение о том, что генеральные характеристики не отклонятся от выборочных на величину большую, чем ошибка выборки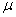 , всегда имеет постоянную степень вероятности, равную 0,683. Значит, в 683 случаях из 1000 характеристика генеральной совокупности будет отличаться от характеристики выборки не больше, чем на величину
, всегда имеет постоянную степень вероятности, равную 0,683. Значит, в 683 случаях из 1000 характеристика генеральной совокупности будет отличаться от характеристики выборки не больше, чем на величину 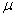 , но в остальных 317 случаях из 1000 она может отличаться и в большей степени.
, но в остальных 317 случаях из 1000 она может отличаться и в большей степени.
Можно повысить вероятность утверждения, расширив пределы отклонений до удвоенной ошибки 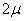 . В примере это значит, что средняя продолжительность горения партии лампочек находится в пределах 300
. В примере это значит, что средняя продолжительность горения партии лампочек находится в пределах 300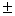 20, т.е. от 280 до 320 часов. Вероятность утверждения в этом случае равна 0,954, т.е. только в 46 случаях из 1000 отклонение выйдет за пределы
20, т.е. от 280 до 320 часов. Вероятность утверждения в этом случае равна 0,954, т.е. только в 46 случаях из 1000 отклонение выйдет за пределы 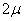 . При утроенной
. При утроенной 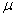 вероятность повышается до 0,997. Значит с определенной степенью вероятности можно утверждать, что отклонения выборочных характеристик от генеральных не превысят некоторой величины, которая называется предельной ошибкой выборки:
вероятность повышается до 0,997. Значит с определенной степенью вероятности можно утверждать, что отклонения выборочных характеристик от генеральных не превысят некоторой величины, которая называется предельной ошибкой выборки:
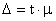 ,
,
где t – нормированное отклонение – коэффициент доверия, зависящий от вероятности, с которой гарантируется, что предельная ошибка  не превысит t – кратную среднюю ошибку.
не превысит t – кратную среднюю ошибку.
Значения доверительной вероятности при различных значениях коэффициента доверия представлены в специально составленных таблицах. Наиболее часто применяемые значения:
t |
1.0 |
1.96 |
2.0 |
2.58 |
3.0 |
Вероятность |
0.683 |
0.95 |
0.954 |
0.99 |
0.997 |
Предельная ошибка выборки позволяет определить доверительные интервалы характеристик генеральной совокупности. Для генеральной средней
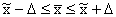 или
или 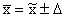 .
.
Это означает, что с заданной вероятностью можно утверждать, что значение генеральной средней следует ожидать в пределах от 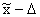 до
до 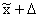 .
.
4. Определение необходимого объема выборки
При проектировании выборочного наблюдения с заранее заданным значением допустимой ошибки выборки одним из наиболее сложных является вопрос о том, сколько единиц изучаемой совокупности необходимо обследовать, чтобы с определенной вероятностью обеспечить точность результатов наблюдения.
Необходимую численность выборки для оценки генеральной средней можно получить из формулы предельной ошибки выборки (предварительно возведя в квадрат обе части равенства). При собственно-случайном или механическом повторном отборе:
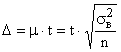 ;
; 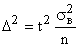 ;
; 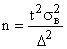 .
.
Для определения необходимой численности выборки должны быть заданы предельная ее ошибка и вероятность того, что эта ошибка не превысит заданного предела. В соответствии с этой вероятностью по таблице находят коэффициент доверия t.
Наиболее сложно определить дисперсию изучаемого признака. Она может быть заимствована из проводимых ранее обследований данной или аналогичной совокупности, а если таковых нет, тогда для определения дисперсии организуют специальное выборочное наблюдение малого объема.
Если такие обследования что отсутствуют, можно воспользоваться соотношением:
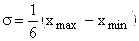 .
.
Для других способов отбора формулы выводятся аналогично.
Таблица 1 – Формулы для нахождения необходимой численности выборки при разных способах отбора
Способ отбора |
Повторный отбор |
Бесповторный отбор |
Собственно-случайный механический |
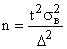
|
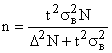
|
Типический |
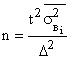
|
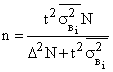
|
Серийный |
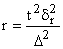
|
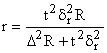
|

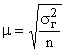 .
.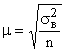 .
.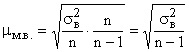 .
.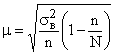 и
и 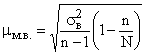 .
.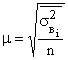 ,
,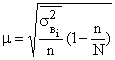 ,
, – средняя из внутригрупповых дисперсий в выборке.
– средняя из внутригрупповых дисперсий в выборке. 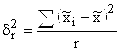
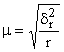 ,
,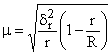 ,
,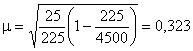
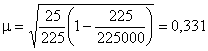
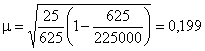
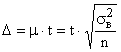 ;
;