По кривой нормального распределения
В анализе распределения большое значение имеет, насколько эмпирическое распределение признака соответствует нормальному. Для этого частоты фактического распределения нужно сравнить с теоретическими, которые характерны для нормального распределения. Значит, нужно по фактическим данным вычислить теоретические частоты кривой нормального распределения, являющиеся функцией нормированных отклонений (см. уравнение кривой 
). Иначе говоря, эмпирическую кривую распределения нужно выравнить кривой нормального распределения.
Порядок расчета теоретических частот кривой нормального распределения:
- по эмпирическим данным рассчитывают среднюю арифметическую ряда
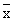и среднее квадратическое отклонение s;
- находят нормированное отклонение t каждой варианты от средней арифметической;
- по таблице распределения функции
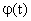определяют ее значения;
- вычисляют теоретические частоты по формуле:
,
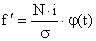где N – объем совокупности,
і – длина интервала;
- строят и сравнивают графики эмпирические и теоретических частот (кривых распределения).
Сумма теоретических и эмпирических частот должна быть равной, но может не совпадать из-за округлений в расчетах.
