При построении статистических моделей наиболее часто применяется нормальное распределение.
Распределение непрерывной случайной величины х называют нормальным, если описывается следующей кривой:
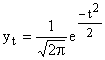
где 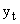 – ордината кривой нормального распределения (частости); – ордината кривой нормального распределения (частости);
е=2,7182 – основание натурального логарифма;
p=3,1415 – постоянное число:
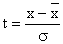 – нормированное отклонение. – нормированное отклонение.
Кривая нормального распределения симметрична относительно 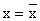 , поэтому величину , поэтому величину 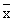 называют центром распределения. На ее вид влияют значения называют центром распределения. На ее вид влияют значения 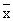 и s. Чем больше s при неизменной и s. Чем больше s при неизменной 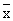 , тем более плоской и растянутой вдоль оси абсцисс становится кривая, и наоборот. , тем более плоской и растянутой вдоль оси абсцисс становится кривая, и наоборот.
Если s остается неизменной, а 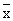 изменяется, то кривые нормального распределения имеют одинаковую форму, но отличаются положением максимальной ординаты. изменяется, то кривые нормального распределения имеют одинаковую форму, но отличаются положением максимальной ординаты.
Особенности кривой нормального распределения (рис.2):
|