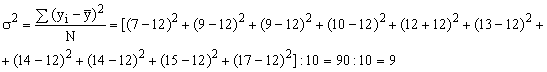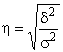Вариационный размах (или размах вариации) - это разница между максимальным и минимальным значениями признака:
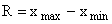
В нашем примере размах вариации сменной выработки рабочих составляет: в первой бригаде R=105-95=10 дет., во второй бригаде R=125-75=50 дет. (в 5 раз больше). Это говорит о том, что выработка 1-й бригады более «устойчива», но резервов роста выработки больше у второй бригады, т.к. в случае достижения всеми рабочими максимальной для этой бригады выработки, ею может быть изготовлено 3*125=375 деталей, а в 1-й бригаде только 105*3=315 деталей.
Если крайние значения признака не типичны для совокупности, то используют квартильный или децильный размахи. Квартильный размах RQ= Q3-Q1 охватывает 50% объема совокупности, децильный размах первый RD1 = D9-D1 охватывает 80% данных, второй децильный размах RD2= D8-D2 – 60 %.
Недостатком показателя вариационного размаха является, но что его величина не отражает все колебания признака.
Простейшим обобщающим показателем, отражающим все колебания признака, является среднее линейное отклонение, представляющее собой среднюю арифметическую абсолютных отклонений отдельных вариант от их средней величины:
для несгруппированных данных
 ,
,
для сгруппированных данных
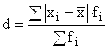 ,
,
где хi – значение признака в дискретном ряду или середина интервала в интервальном распределении.
В вышеприведенных формулах разности в числителе взяты по модулю, иначе, согласно свойству средней арифметической, числитель всегда будет равен нулю. Поэтому среднее линейное отклонение в статистической практике применяют редко, только в тех случаях, когда суммирование показателей без учета знака имеет экономический смысл. С его помощью, например, анализируется состав работающих, рентабельность производства, оборот внешней торговли.
Дисперсия признака – это средний квадрат отклонений вариант от их средней величины:
простая дисперсия
 ,
,
взвешенная дисперсия
 .
.
Формулу для расчета дисперсии можно упростить:

Таким образом, дисперсия равна разности средней из квадратов вариант и квадрата средней из вариант совокупности:
 .
.
Однако, вследствие суммирования квадратов отклонений дисперсия дает искаженное представление об отклонениях, поэтому ее на основе рассчитывают среднее квадратическое отклонение, которое показывает, на сколько в среднем отклоняются конкретные варианты признака от их среднего значения. Вычисляется путем извлечения квадратного корня из дисперсии:
для несгруппированных данных
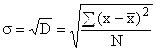 ,
,
для вариационного ряда

Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее совокупность, тем более надежной (типичной) будет средняя величина.
Среднее линейное и среднее квадратичное отклонение - именованные числа, т. е. выражаются в единицах измерения признака, идентичны по содержанию и близки по значению.
Рассчитывать абсолютные показатели вариации рекомендуется с помощью таблиц.
Таблица 3 – Расчет характеристик вариации (на примере срока данных о сменной выработке рабочих бригады)
Группы рабочих по выработке, шт. |
Число рабочих, 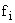 |
Середина интервала, 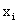 |
Расчетные значения |
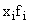
|
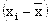
|
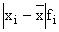
|
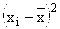
|

|
170-190 |
10 |
180 |
1800 |
-36 |
360 |
1296 |
12960 |
190-210 |
20 |
200 |
4000 |
-16 |
320 |
256 |
5120 |
210-230 |
50 |
220 |
11000 |
4 |
200 |
16 |
800 |
230-250 |
20 |
240 |
4800 |
24 |
480 |
576 |
11520 |
Итого: |
100 |
- |
21600 |
- |
1360 |
- |
30400 |
Среднесменная выработка рабочих:
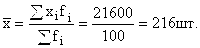
Среднее линейное отклонение:
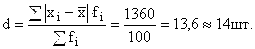
Дисперсия выработки:
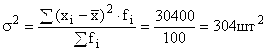
Среднее квадратическое отклонение выработки отдельных рабочих от средней выработки:
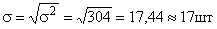 .
.
1 Расчет дисперсии способом моментов
Вычисление дисперсий связано с громоздкими расчетами (особенно если средняя величина выражена большим числом с несколькими десятичными знаками). Расчеты можно упростить, если использовать упрощенную формулу и свойства дисперсии.
Дисперсия обладает следующими свойствами:
- если все значения признака уменьшить или увеличить на одну и ту же величину А, то дисперсия от этого не уменьшится:
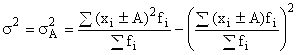 ,
,
- если все значения признака уменьшить или увеличить в одно и то же число раз (h раз), то дисперсия соответственно уменьшится или увеличится в
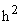 раз. То есть, если дисперсию уменьшенных значений признака описать следующим выражением
раз. То есть, если дисперсию уменьшенных значений признака описать следующим выражением
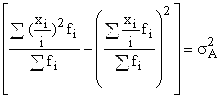 , то
, то 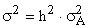 или
или 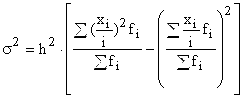
Используя свойства дисперсии и сначала уменьшив все варианты совокупности на величину А, а затем разделив на величину интервала h, получим формулу вычисления дисперсии в вариационных рядах с равными интервалами способом моментов:
 ,
,
где 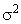 – дисперсия, исчисленная по способу моментов;
– дисперсия, исчисленная по способу моментов;
h – величина интервала вариационного ряда;
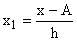 – новые (преобразованные) значения вариант;
– новые (преобразованные) значения вариант;
А – постоянная величина, в качестве которой используют середину интервала, обладающего наибольшей частотой; либо вариант, имеющий наибольшую частоту;
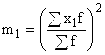 – квадрат момента первого порядка;
– квадрат момента первого порядка;
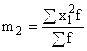 – момент второго порядка.
– момент второго порядка.
Выполним расчет дисперсии способом моментов на основе данных о сменной выработке рабочих бригады.
Таблица 4 – Расчет дисперсии по способу моментов
Группы рабочих по выработке, шт. |
Число рабочих, 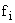 |
Середина интервала, 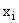 |
Расчетные значения |
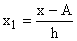
|
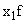
|
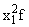
|
170-190 |
10 |
180 |
-2 |
-20 |
40 |
190-210 |
20 |
200 |
-1 |
-20 |
20 |
210-230 |
50 |
220 |
0 |
0 |
0 |
230-250 |
20 |
240 |
1 |
20 |
20 |
Итого |
100 |
- |
- |
-20 |
80 |
Порядок расчета:
- определяем постоянное число А, это варианта с наибольшей частотой: А=220;
- определяем
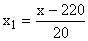 ;
;
- рассчитываем
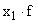 и
и 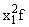 ;
;
- определяем моменты 1-го и 2-го порядка:
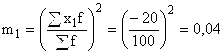

- рассчитываем дисперсию:
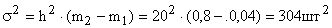
2 Расчет дисперсии альтернативного признака
Среди признаков, изучаемых статистикой, есть и такие, которым свойственны лишь два взаимно исключающих значения. Это альтернативные признаки. Им придается соответственно два количественных значения: варианты 1 и 0. Частостью варианты 1, которая обозначается p, является доля единиц, обладающих данным признаком. Разность 1-р=q является частостью варианты 0. Таким образом,
Средняя арифметическая альтернативного признака
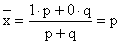 , т. к. p+q=1.
, т. к. p+q=1.
Дисперсия альтернативного признака
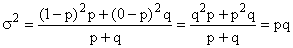 , т.к. 1-р=q
, т.к. 1-р=q
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц, не обладающих этим признаком.
Если значения 1 и 0 встречаются одинаково часто, т. е. p=q, дисперсия достигает своего максимума pq=0,25.
Дисперсия альтернативного признака используется в выборочных обследованиях, например, качества продукции.
3 Межгрупповая дисперсия. Правило сложения дисперсий
Дисперсия, в отличие от других характеристик вариации, является аддитивной величиной. То есть в совокупности, которая разделена на группы по факторному признаку х, дисперсия результативного признака y может быть разложена на дисперсию в каждой группе (внутригрупповую) и дисперсию между группами (межгрупповую). Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучение вариации в каждой группе, а также между этими группами.
Общая дисперсия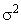 измеряет вариацию признака у по всей совокупности под влиянием всех факторов, вызвавших эту вариацию (отклонения). Она равна среднему квадрату отклонений отдельных значений признака у от общей средней
измеряет вариацию признака у по всей совокупности под влиянием всех факторов, вызвавших эту вариацию (отклонения). Она равна среднему квадрату отклонений отдельных значений признака у от общей средней 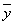 и может быть вычислена как простая или взвешенная дисперсия.
и может быть вычислена как простая или взвешенная дисперсия.
Межгрупповая дисперсия 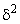 характеризует вариацию результативного признака у, вызванную влиянием признака-фактора х, положенного в основу группировки. Она характеризует вариацию групповых средних и равна среднему квадрату отклонений групповых средних
характеризует вариацию результативного признака у, вызванную влиянием признака-фактора х, положенного в основу группировки. Она характеризует вариацию групповых средних и равна среднему квадрату отклонений групповых средних 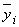 от общей средней
от общей средней 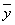 :
:
 ,
,
где 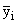 – средняя арифметическая i-той группы;
– средняя арифметическая i-той группы;
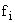 – численность единиц в i-той группе (частота i-той группы);
– численность единиц в i-той группе (частота i-той группы);
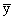 – общая средняя совокупности.
– общая средняя совокупности.
Внутригрупповая дисперсия 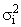 отражает случайную вариацию, т. е. ту часть вариации, которая вызвана влиянием неучтенных факторов и не зависит от признака-фактора, положенного в основу группировки. Она характеризует вариацию индивидуальных значений относительно групповых средних, равна среднему квадрату отклонений отдельных значений признака у внутри группы от средней арифметической этой группы (групповой средней)
отражает случайную вариацию, т. е. ту часть вариации, которая вызвана влиянием неучтенных факторов и не зависит от признака-фактора, положенного в основу группировки. Она характеризует вариацию индивидуальных значений относительно групповых средних, равна среднему квадрату отклонений отдельных значений признака у внутри группы от средней арифметической этой группы (групповой средней) 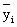 и вычисляется как простая или взвешенная дисперсия для каждой группы:
и вычисляется как простая или взвешенная дисперсия для каждой группы:
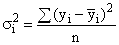 или
или 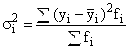 ,
,
где 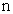 – число единиц в группе.
– число единиц в группе.
На основании внутригрупповых дисперсий по каждой группе можно определить общую среднюю из внутригрупповых дисперсий:
 .
.
Взаимосвязь между тремя дисперсиями получила название правила сложения дисперсий, согласно которому общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий:
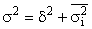
Пример. При изучении влияния тарифного разряда (квалификации) рабочих на уровень производительности их труда получены следующие данные.
Таблица 5 – Распределение рабочих по среднечасовой выработке.
№
п/п |
Рабочие 4-го разряда |
№
п/п |
Рабочие 5-го разряда |
Выработка
рабочего, шт., 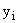 |
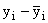
|
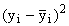
|
Выработка
рабочего, шт., 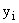 |
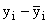
|
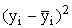
|
1
2
3
4
5
6 |
7
9
9
10
12
13 |
7-10=-3
9-10=-1
-1
0
2
3 |
9
1
1
0
4
9 |
1
2
3
4
|
14
14
15
17
|
14-15=-1
-1
0
2
|
1
1
0
4
|
|
60 |
- |
24 |
S |
60 |
- |
6 |
В данном примере рабочие разделены на две группы по факторному признаку х– квалификации, которая характеризуется их разрядом. Результативный признак 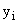 – выработка – варьируется как под его влиянием (межгрупповая вариация), так и за счет других случайных факторов (внутригрупповая вариация). Задача заключается в измерении этих вариаций с помощью трех дисперсий: общей, межгрупповой и внутригрупповой.
– выработка – варьируется как под его влиянием (межгрупповая вариация), так и за счет других случайных факторов (внутригрупповая вариация). Задача заключается в измерении этих вариаций с помощью трех дисперсий: общей, межгрупповой и внутригрупповой.
- Определяем групповые и общую средние выработки, шт:
по первой группе  шт.,
шт.,
по второй группе 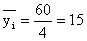 шт.,
шт.,
по двум группам 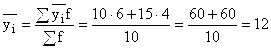 шт.
шт.
- Рассчитываем и заносим в таблицу
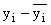 и
и 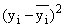 .
.
- Рассчитываем внутригрупповые дисперсии:
по первой группе 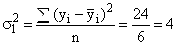 ,
,
по второй группе 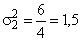
Внутригрупповые дисперсии показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (состояние оборудования, обеспеченность материалами и инструментами, возраст рабочих и т. д), кроме различий в квалификации, т. к. внутри группы все рабочие имеют одинаковый разряд.
- Вычисляем среднюю из внутригрупповых дисперсий:
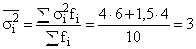
Средняя дисперсия отражает вариацию выработки, обусловленную всеми факторами, кроме квалификации, но в среднем по совокупности.
- Межгрупповая дисперсия, характеризует вариацию среднегрупповых выработок, вызванную различием групп рабочих по квалификационному разряду:
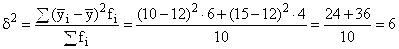
- Вычисляем общую дисперсию совокупности, которая отражает суммарное влияние всех возможных факторов на общую вариацию выработки изделий всеми рабочими:
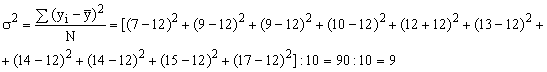
- Определяем общую дисперсию по правилу сложения дисперсий:
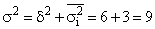
Очевидно, что чем выше доля межгрупповой дисперсии 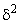 в общей дисперсии
в общей дисперсии 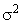 , тем сильнее влияние факторного признака (разряда) на результативный (выработку).
, тем сильнее влияние факторного признака (разряда) на результативный (выработку).
Эта доля характеризуется эмпирическим коэффициентом детерминации:
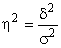
Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х. Остальная часть общей вариации у вызвана изменением прочих факторов.
В примере эмпирический коэффициент детерминации равен:
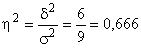 или 66,7 %,
или 66,7 %,
Это означает, что на 66,7% вариация производительности труда рабочих обусловлена различиями в квалификации, а на 33,3% – влиянием прочих факторов.
Эмпирическое корреляционное отношение показывает тесноту связи между группировочным и результативными признаками. Рассчитывается как корень квадратный из эмпирического коэффициента детерминации:
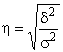
Эмпирическое корреляционное отношение 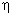 , как и
, как и 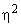 , может принимать значения от 0 до 1.
, может принимать значения от 0 до 1.
Если связь отсутствует, то 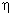 =0. В этом случае
=0. В этом случае 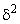 =0, то есть групповые средние равны между собой и межгрупповой вариации нет. Значит группировочный признак – фактор не влияет на образование общей вариации.
=0, то есть групповые средние равны между собой и межгрупповой вариации нет. Значит группировочный признак – фактор не влияет на образование общей вариации.
Если связь функциональная, то 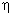 =1. В этом случае дисперсия групповых средних равна общей дисперсии (
=1. В этом случае дисперсия групповых средних равна общей дисперсии (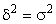 ), то есть внутригрупповой вариации нет. Это означает, что группировочный признак полностью определяет вариацию изучаемого результативного признака.
), то есть внутригрупповой вариации нет. Это означает, что группировочный признак полностью определяет вариацию изучаемого результативного признака.
Чем ближе значение корреляционного отношения к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
Для качественной оценки тесноты связи между признаками пользуются соотношениями Чэддока.
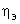 |
0 |
0-0,2 |
0,2-0,3 |
Сила связи |
отсутствует |
очень слабая |
слабая |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
1 |
умеренная |
заметная |
тесная |
весьма тесная |
функцио-
нальная |
В примере 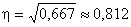 , что свидетельствует о тесной связи между производительностью труда рабочих и их квалификацией.
, что свидетельствует о тесной связи между производительностью труда рабочих и их квалификацией.

 .
.
 .
.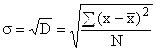 ,
,
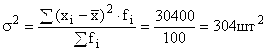
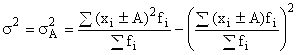 ,
, , то
, то 
 ,
,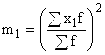 – квадрат момента первого порядка;
– квадрат момента первого порядка; 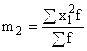 – момент второго порядка.
– момент второго порядка.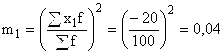

 ,
,