Решение cистем уравнений в Derive

Систему линейных уравнений можно задать непосредственно в командной строке в виде вектора-строки или вектора-столбца, как записано ниже для u.

u := [5*x + 3*y - 3*z = -10; 7*x - 4*y + 3*z = 20; 3*x + 3*y - 5*z = -26];

SOLVE(u, [x, y, z])                       [x = 1 ^ y = 2 ^ z = 7];

SOLUTIONS(u, [x, y, z])              [[1, 2, 7]].

Матричное представление системы линейных уравнений также допустимо. Пусть матрица коэффициентов, вектор правых частей и вектор искомых переменных последовательно определены через командную строку следующим образом:

A1 := [5, 3, -3; 7, -4, 3; 3, 3, -5];

B := [-10, 20, -26];

X := [x1, x2, x3].

Систему уравнений, обозначенную именем U, и именованные операторы решения этой системы можно ввести так:

U:=A*[X]` = [B]`;

Sv := SOLVE(A1*[X]` = [B]`, X)                     Sv := x1 = 1 ^ x2 = 2 ^ x3 = 7;

St := SOLUTIONS(A1*[X]` = [B]`, X)             St := [[1, 2, 7]].

Имена функциям вводятся для удобного обращения к результату. Если правых частей системы много, то их можно представить в виде матрицы и составить функцию, которая последовательно найдет решения системы для каждой правой части. Для примера определим матрицу правых частей и решающую функцию так:

C := [-10, 20, -26; -100, 200, -260; 1, 2, 3; 3, 2, 1];

VS:=VECTOR(SOLUTIONS(A1*[X]` = [C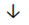i]`, X), i, 1, 4);

VS := [[1, 2, 7]; [10, 20, 70]; [7/44, - 12/11, - 51/44]; [21/44, 8/11, 23/44]].