Сумматор - это лектронная логическая схема (рис. 3.8), формирующая сигналы суммы (S) и переноса (Р) при сложении двух двоичных чисел (А, В) и сигнала переноса соседнего младшего разряда (С) по правилам двоичной арифметики (см. таблицу 3.3).
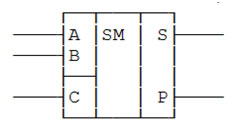
Рис. 3.8 - Одноразрядный сумматор
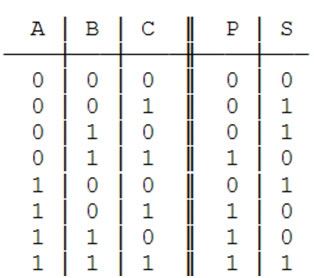
Таблица 3.3 -Таблица состояний одноразрядного сумматора
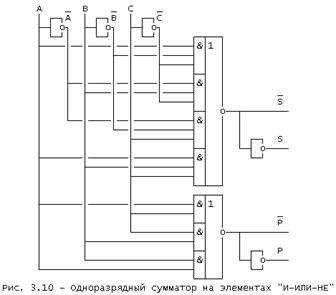
Принципиальная схема одноразрядного сумматора, реализованная на элементах "И-ИЛИ-НЕ", приведена на рис. 3.10.
Более простая схема сумматора может быть реализована с учетом соотношения : сигнал суммы (S) равен единице, если только один входной сигнал (А, В, С) равен единице и отсутствует перенос (Р) или все три входных сигнала равны единице :
_ _ _
S = A P + B P + C P + A B C (3.7)
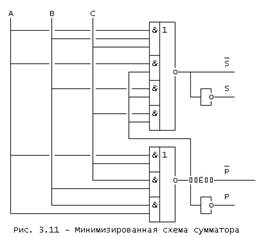
Упрощенная схема одноразрядного сумматора, реализующая функцию (3.7), приведена на рис. 3.11. В этой схеме время задержки распространения сигнала суммы (S) больше, чем время задержки сигнала переполнения (Р).
Логический элемент "И-ИЛИ-НЕ" имеется в наборе любой серии ТТЛ и ТТЛШ (см. рис. 2.16). Для КМОП элементов эти схемы сумматоров легко реализуются в базисе "И-НЕ".
На основе одноразрядного сумматора реализуются схемы многоразрядных сумматоров. На рис. 3.12 приведена схема четырехразрядного сумматора (аналогично можно реализовать сумматор на 8 или 16 разрядов). На входы А1..А4 подается первое слагаемое (младший разряд - А1), на входы В1..В4 - второе. Вход переноса (С) младшего разряда подключен к нулевому логическому уровню (к общей шине).Четыре разряда суммы формируются на выходах S1..S4, пятый разряд суммы - на выходе Р4.
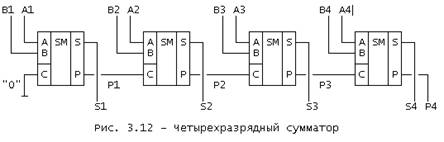
В формировании сигналов S4, P4 участвуют все входные переменные А1..А4, В1..В4. Но ко входам последней логической схемы эти сигналы проходят через разное количество элементов, что вызывает появление на выходах ложных коротких импульсов, образованных эффектом гонок (состязаний).
Многоразрядный сумматор с последовательным переносом. Таким образом, в общем случае для каждого разряда необходима логическая схема с тремя входами ai, bi, Ci и двумя выходами Si, Ci+1. Такая схема и есть полный сумматор. Ее можно реализовать с помощью двух полусумматоров.
Входы |
Промежуточные величины |
Выходы |
ai |
bi |
сi |
Pi |
gi |
ri |
Si |
Ci+1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
Для сложения двух многоразрядных двоичных чисел на каждый разряд необходим один полный сумматор. Только в младшем разряде можно обойтись полусумматором. На рис. 2.23 приведена схема, предназначенная для сложения двух четырехразрядных чисел А и В. Эта схема выпускается в интегральном исполнении. В ее младшем разряде также используется полный сумматор, чтобы иметь возможность наращивания разрядности схемы.
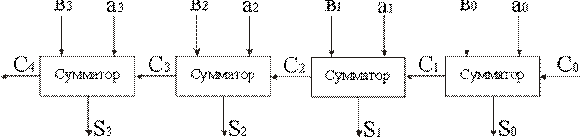
Рис. 2.23. Сумматор с последовательным переносом
Сумматоры с параллельным переносом. Время выполнения операции в сумматоре с параллельным переносом намного больше времени сложения в одноразрядном сумматоре. Действительно, сигнал переноса С4 только тогда может принять истинное значение, когда будет установлено правильное значение С3. Такой порядок выполнения операций называется последовательным переносом (Ripple Carry).
Чтобы уменьшить время операции сложения многоразрядных чисел можно использовать схемы параллельного переноса (Carry look-ahead). При этом все сигналы переноса вычисляются непосредственно по значениям входных переменных.
Согласно таблице переключений, в общем случае для сигнала переноса любого i-го разряда справедливо соотношение:
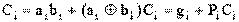 . (1)
. (1)
Величины gi, ri вычисляются в качестве промежуточных результатов и в полном сумматоре. Следовательно, их получение не требует дополнительных затрат. Смысл этих величин объясняется совсем просто. Сигнал gi вырабатывается тогда, когда в данном разряде перенос происходит из-за комбинации входных переменных ai,bi. Поэтому его называют функцией генерации переноса. Сигнал Pi показывает, передается ли полученный в младшем разряде сигнал переноса Ci дальше. Поэтому он называется функцией распространения переноса.
Пользуясь выражением (1), можно вывести следующие формулы для вычисления сигналов переноса:
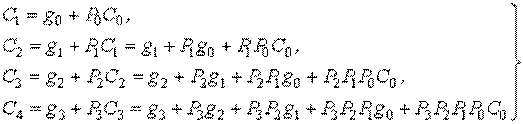 (2)
(2)
Очевидно, что хотя полученные выражения достаточно сложные, время формирования сигнала переноса в любой разрад с помощью вспомогательных функций определяется только времением здержки распространения сигнала на двух элементах. Эти функции реализуются специальным комбинационным устройством – схемой ускоренного переноса.
Схема сумматора с параллельным переносом приведена на рис. 2.24, а. На рис. 2.24, б изображена схема устройства параллельного переноса в группе из четырех разрядов. Эта схема реализует систему уравнений (2).
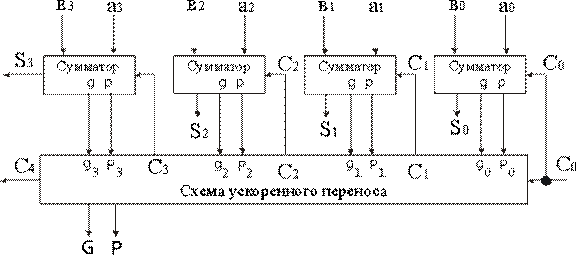
Рис. 2.24. Схема сумматора с параллельным переносом







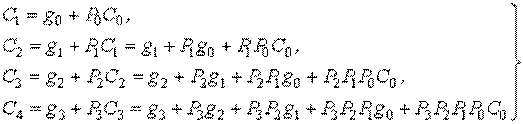 (2)
(2) 