Задание:
1. В целочисленном интервале [5, 10] рассчитать таблицу значений для выражения, заданного с помощью следующих таблиц, :
Таблица 1
Выражение |
|
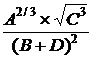
Таблица 2
2. Выполнить задание 1, используя негативный шаг - 1.
3. Отобразить в линейном масштабе на одних осях два графика функции 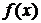 из задания один с шагами 1.0 и 0.05 в интервале [5, 10].
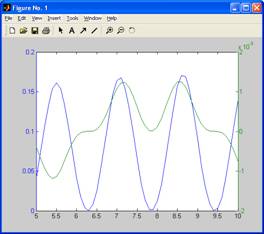
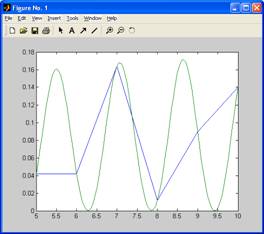
С помощью функции plotyy постройте с шагом 0.1 в интервале [5, 10] графика функци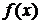й  и  .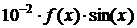
4. Выполните задание 3, используя:
- логарифмический масштаб по обеим осям;
- логарифмический масштаб по оси абсцисс;
- логарифмический масштаб по оси ординат.
При выполнении этого пункта используйте шесть типов маркеров, шесть разных цветов линий и разные типы линий.
5. Сформируйте матрицу и вектор размерами соответственно не менее 5x6 и 1x7, первыми элементами которых является Ваш номер по списку в журнале группы. Постройте графику вектора и матрицы.
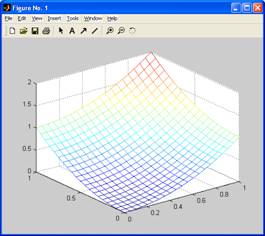
6. Приведите график функции z(x, у)= х2 + у2 на области определения в виде квадрата х є [0, 1], y є [0, 1] с шагом 0.2 и график функции с меньшим шагом сетки.
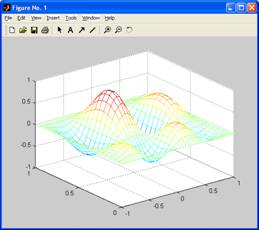
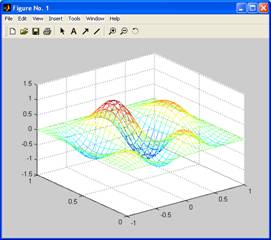
7. Постройте прозрачную и непрозрачную каркасную поверхность для функции 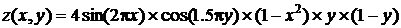 на прямоугольной области определения х є [l, l], y є [0, l].
Измените функцию 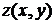 каким-либо способом, но таким, чтобы в выражении функции фигурировал Ваш номер по списку в журнале группы. Приведите в отчете прозрачную и непрозрачную каркасную поверхность для Вашей функции.
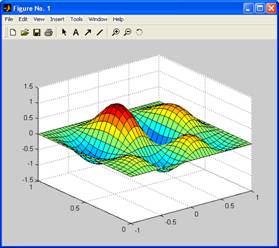
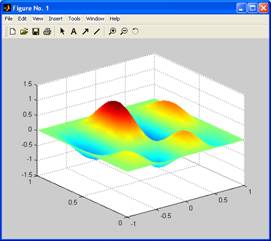
8. Постройте каркасную поверхность функции 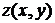 с помощью команд surf(X, y, z), shading flat, shading interp и приведите их в отчете.
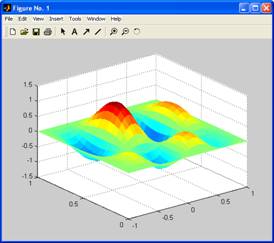
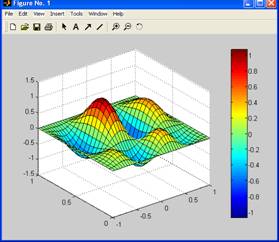
9. Постройте каркасную поверхность функции 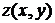 с помощью команд surf(x, y, z) и colorbar. Результаты приведите в отчете.
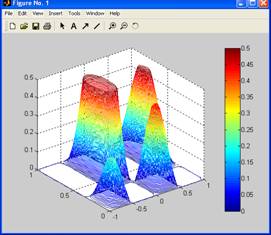
10. Постройте каркасную поверхность функции 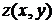 с помощью команд surfс, meshc и colorbar. Результаты приведите в отчете.
11. Постройте поверхности функции, которые состоят из линий уровня, с помощью функции contour3 с тремя и четырьмя аргументами. Результаты приведите в отчете.
12. Постройте контурную графику функции с помощью функций contour, contourf, clabel. Результаты приведите в отчете.
13. Выполните три разных цветовых оформления графика функции . Результаты приведите в отчете.
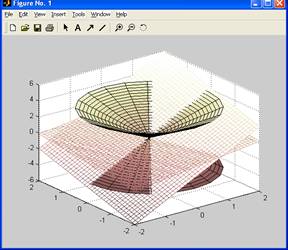
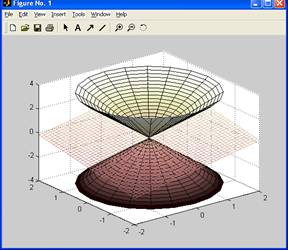
14. Выполните построение рядового конуса и плоскости по указаниям подразделения 2.6 методических указаний.
15. Выполните пересечение конуса двумя разными плоскостями.
16. Оформить отчет по лабораторной работе. Если объем отчета будет превышать 6 страниц или будет использоваться монохромная печать, то приведите в отчете наиболее интересные результаты, а полный отчет представьте в электронном виде.
Программа:
N = 5
A = (sin(N)*cos(N))^2
A =
0.0740
t = exp(1)
B = (log(N+2)/log(t))/N
B =
0.3892
C = 1/(exp(1/N))^2
C =
0.6703
D = A + B
D =
0.4632
W = [0,0,0,0,0]
for i = 1:5
A = (sin(N)*cos(N))^2
B = (log(N+2)/log(t))/N
C = 1/(exp(1/N))^2
D = A + B
W(i) = A^(2/3)*C^(1/3)/(B+D)^2
N = N + 1
end
A =
0.0740
B =
0.3892
C =
0.6703
D =
0.4632
W =
0.2123 0.5540 0.4674 0.2546 0
N =
6
A =
0.0720
B =
0.3466
C =
0.7165
D =
0.4186
W =
0.2123 0.2645 0.4674 0.2546 0
N =
7
A =
0.2453
B =
0.3139
C =
0.7515
D =
0.5592
W =
0.2123 0.2645 0.4674 0.2546 0
N =
8
A =
0.0207
B =
0.2878
C =
0.7788
D =
0.3085
W =
0.2123 0.2645 0.4674 0.1952 0
N =
9
A =
0.1410
B =
0.2664
C =
0.8007
D =
0.4074
W =
0.2123 0.2645 0.4674 0.1952 0.5540
N= 10
N =
10
for i = 1:5
A = (sin(N)*cos(N))^2
B = (log(N+2)/log(t))/N
C = 1/(exp(1/N))^2
D = A + B
W(i) = A^(2/3)*C^(1/3)/(B+D)^2
N = N - 1
end
A =
0.2084
B =
0.2485
C =
0.8187
D =
0.4569
W =
0.6609 0.2645 0.4674 0.1952 0.5540
N =
9
A =
0.1410
B =
0.2664
C =
0.8007
D =
0.4074
W =
0.6609 0.5540 0.4674 0.1952 0.5540
N =
8
A =
0.0207
B =
0.2878
C =
0.7788
D =
0.3085
W =
0.6609 0.5540 0.1952 0.1952 0.5540
N =
7
A =
0.2453
B =
0.3139
C =
0.7515
D =
0.5592
W =
0.6609 0.5540 0.1952 0.4674 0.5540
N =
6
A =
0.0720
B =
0.3466
C =
0.7165
D =
0.4186
W =
0.6609 0.5540 0.1952 0.4674 0.2645
N =
5
N_ = [5:0.05:10];
A1=(sin(N_).*cos(N_)).^(2);
B1 = (log(N_+2)/log(t))./N_;
C1 = (exp(1./N_)).^-2;
D1 = A1 + B1;
Z1 = ((A1.*C1).*((D1).^(1/3)))./(C1.^(2/3)+B1.^2);
N = [5:10]
N =
5 6 7 8 9 10
A = (sin(N).*cos(N)).^(2)
A =
0.0740 0.0720 0.2453 0.0207 0.1410 0.2084
B = (log(N+2)/log(t))./N
B =
0.3892 0.3466 0.3139 0.2878 0.2664 0.2485
C = (exp(1./N)).^-2
C =
0.6703 0.7165 0.7515 0.7788 0.8007 0.8187
D = A + B
D =
0.4632 0.4186 0.5592 0.3085 0.4074 0.4569
F = ((A.*C).*((D).^(1/3)))./(C.^(2/3)+B.^2)
F =
0.0418 0.0419 0.1642 0.0117 0.0897 0.1402
plot( N, F, N_ ,Z1 )
N=[5:0.1:10];
A = (sin(N).*cos(N)).^(2);
B = (log(N+2)/log(t))./N;
C = (exp(1./N)).^-2;
D = A + B;
F = ((A.*C).*((D).^(1/3)))./(C.^(2/3)+B.^2);
F2=(0.01*F).*sin(N);
plotyy(N,F,N,F2)
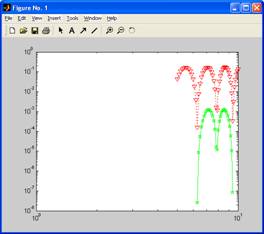
loglog(N,F,'rv:',N,F2,'gp-')
Warning: Negative data ignored.
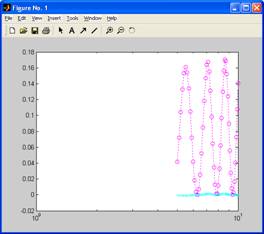
semilogx(N,F,'mo:',N,F2,'cx')
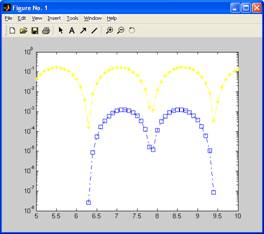
semilogy(N,F,'y*--',N,F2,'bs-.')
Warning: Negative data ignored.
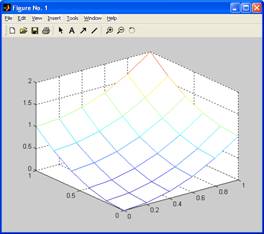
[X, Y] = meshgrid(0:0.2:1,0:0.2:1);
Z = X.^2+Y.^2;
mesh(X,Y,Z);
[X, Y] = meshgrid(0:0.05:1,0:0.05:1);
Z = X.^2+Y.^2;
mesh(X,Y,Z)
[X, Y] = meshgrid(-1:0.05:1, 0:0.05:1);
Z = 4*sin(2*pi*X).*cos(1.5*pi*Y).*(1-X.^2).*Y.*(1-Y);
mesh(X,Y,Z)
[X, Y] = meshgrid(-1:0.05:1, 0:0.05:1);
mesh(X,Y,Z)
Z = 5*sin(2*pi*X).*cos(1.5*pi*Y).*(1-X.^2).*Y.*(1-Y);
mesh(X,Y,Z)
hidden off
mesh(X,Y,Z)
hidden off
hidden on
surf(X,Y,Z)
shading flat
shading interp
shading faceted
surf(X,Y,Z)
colorbar
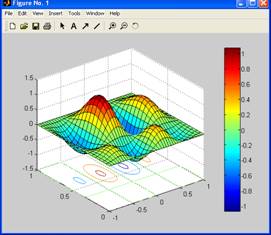
surfc(X,Y,Z)
colorbar
levels = [0:0.01:0.5];
contour3(X, Y, Z, levels)
colorbar
levels = [0:0.005:0.5];
contour3(X, Y, Z, levels)
colorbar
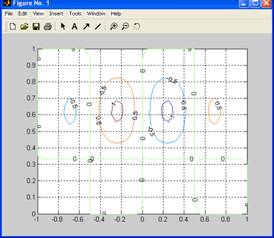
contour(X,Y,Z)
colorbar
[CMatr, h] = contour(X, Y, Z);
clabel(CMatr, h)
grid on
contour(X,Y,Z)
contour3(X, Y, Z, levels)
contourf(X, Y, Z, 20)
colorbar
surfc(X, Y, Z)
colorbar
colormap(gray)
title('Grafik funktsii z(x,y)')
xlabel('x')
ylabel('y')
zlabel('z')
u = [-2*pi:0.1*pi:2*pi]';
v = [-2*pi:0.1*pi:2*pi];
x = 0.3*u*cos(v);
y = 0.3*u*sin(v);
z = 0.6*u*ones(size(v));
surf(x, y, z)
colormap(pink)
[x,y] = meshgrid(-2:0.1:2);
z = 0.5*x+0.4*y;
hold on
mesh(x, y, z)
hidden off
z = 2*x+y;
hold on
mesh(x, y, z)
exit
Результат роботи программы:
 
 
 
 
 
 
 
 
 
 
|
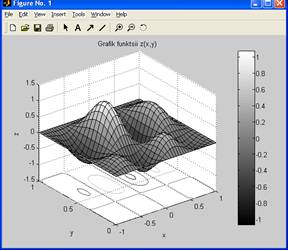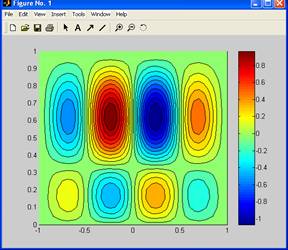
