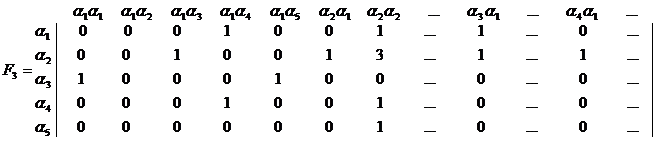Одной из важнейших особенностей применения вычислительной техники является использование огромного количества различных прикладных и научных программ, разработанных на основе множества специализированных математических и технических дисциплин. Ограниченность возможностей человеческого разума уже давно не позволяет охватить всю доступную совокупность знаний по различным математическим методам решения задач и приводит к тому, что специалист овладевает все меньшей их частью. С накоплением знаний это приводит к более узкой специализации, которая очень затрудняет решение задач, находящихся на стыке нескольких специальностей. Однако именно такие типы задач в настоящее время приобретают все большее значение. Одним из важнейших типов подобных задач являются задачи моделирования различных природных и технических объектов и процессов, которые, как правило, требуют привлечения специалистов по численным методам и хорошо владеющих изучаемым объектом. Традиционные подходы к разработке математических моделей сложных объектов и алгоритмов решения проблемных задач обычно требуют на свое осуществление годы. Поскольку такое положение не соответствует современным темпам развития общества в последние десятилетия предпринимались интенсивные попытки создания более универсальных подходов к синтезу математических моделей и решению других сложных задач.
Один из этих подходов связан с рассмотрением человеческого интеллекта как продукта естественного эксперимента природы, в результате которого за миллиарды лет осуществлена эволюция от простейших живых организмов до современного человека. Конечный результат длительного эволюционного процесса в природе дает основание допускать, что в настоящее время, быть может, важнее моделировать не интеллект человека, а процесс, который привел к появлению этого интеллекта. Моделирование процесса эволюции осуществлялось многократно, но только с появлением работы американских ученых Фогеля, Оуэнса, Уолша [1] в науке об искусственном интеллекте появилось новое направление, заменяющее процесс моделирования интеллекта человека на моделирование процесса эволюции человеческого интеллекта. Творцы нового научного направления рассчитывали при этом на более глубокое изучение важнейших свойств интеллекта, а главное – на получение универсального средства «для синтеза машин, обнаруживающих большую «разумность», чем до сих пор удалось найти в природе» [1]. По мнению авторов, разумное поведение – это не что иное, как умение прогнозировать состояние внешней среды для того, чтобы на основе правильного прогноза оптимизировать поведение для достижения заданных целей. В качестве объектов эволюции выбраны конечные автоматы, на входы которых поступают сигналы из внешней среды, представляющие собой источник последовательных 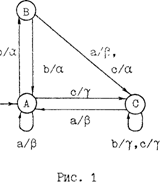 сигналов из конечного алфавита. На рис. 1 представлен конечный автомат М с тремя состояниями A, B, C алфавит входных символов автомата состоит из символов а, b, с, а выходных – из
сигналов из конечного алфавита. На рис. 1 представлен конечный автомат М с тремя состояниями A, B, C алфавит входных символов автомата состоит из символов а, b, с, а выходных – из  ,
,  ,
, 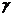 (входные символы приведены слева от наклонных черт, а выходные – справа, стрелкой отмечено начальное состояние автомата). Рассмотрим работу автомата при поступлении на его вход последовательности символов b, a, c, c, a, b, b, a, c, a. Входной символ b, поданный на вход автомата в начальном состоянии А, приводит к появлению на выходе автомата символа
(входные символы приведены слева от наклонных черт, а выходные – справа, стрелкой отмечено начальное состояние автомата). Рассмотрим работу автомата при поступлении на его вход последовательности символов b, a, c, c, a, b, b, a, c, a. Входной символ b, поданный на вход автомата в начальном состоянии А, приводит к появлению на выходе автомата символа 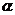 и переходу автомата в состояние B. Следующий входной символ приходит на вход автомата только после того, как в автомате закончатся все переходные процессы. Второй символ а входной последовательности переводит автомат в состояние C с появлением на выходе автомата символа
и переходу автомата в состояние B. Следующий входной символ приходит на вход автомата только после того, как в автомате закончатся все переходные процессы. Второй символ а входной последовательности переводит автомат в состояние C с появлением на выходе автомата символа 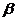 . Покажем последовательность изменения состояний автомата и выходных символов при заданной входной последовательности:
. Покажем последовательность изменения состояний автомата и выходных символов при заданной входной последовательности:
Отсюда видно, что автомат преобразует последовательность входных символов в последовательность выходных символов. При прогнозировании состояний внешней среди автомат должен иметь одинаковые входной и выходной алфавиты. Он может прогнозировать как следующий символ входной последовательности, поступающий на следующем такте работы автомата, так и любой другой символ с заданным числом тактов упреждения. Рассмотрим случай, когда автомат м прогнозирует следующий символ входной последовательности. При этом полагаем, что a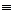
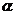 , b
, b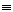
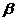 , c
, c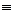
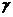 , а стоимость ошибки равна единице при любом неправильном предсказании следующего входного символа и равна нулю при правильном предсказании. При функционировании автомата видно, что автомат правильно предсказал четыре входных символа и сделал пять ошибок:
, а стоимость ошибки равна единице при любом неправильном предсказании следующего входного символа и равна нулю при правильном предсказании. При функционировании автомата видно, что автомат правильно предсказал четыре входных символа и сделал пять ошибок:
Текущее состояние A B C C C A B A A C |
Входной символ b a c c a b b a c a |
Выходной символ a b c c b a a b c b |
Стоимость ошибки 0 1 0 1 0 1 0 1 1 |
В эволюционном моделировании потомки автоматов получают путем случайных мутаций исходного автомата - добавляют или убирают одно или несколько состояний конечного автомата, изменяют начальное состояние автомата, изменяют конечное состояние у одного или нескольких ребер, входные и (или) выходные символы, соответствующие случайно выбранным ребрам автомата, и так далее. Полученные таким образом потомки оценивают на той же последовательности и, если они превосходят родительский автомат по заданному критерию, то один или несколько лучших автоматов оставляют для последующей работы, а остальные автоматы, включая и родительский, отбрасывают. Процесс мутаций повторяется до тех пор, пока не будет достигнуто определенное значение критерия качества функционирования автомата на заданной предыстории. Полученный в результате такого процесса автомат может использоваться для предсказания среды в реальном времени.
Известно множество экспериментов с предсказанием как простых входных последовательностей (например, детерминированных циклических последовательностей), так и более сложных: стационарных статистических последовательностей (например, предсказание последовательности, которая получена в результате бросания асимметричной монеты с заданной вероятностью 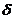 выпадения герба) или нестационарных случайных последовательностей (например, предсказание последовательности 0,1,1,1,0,1,0,1,0,0,0,1, … , полученной в результате классификации чисел натурального ряда 0,1,2,3,4,5,6,7,8,9,10,11, … на простые, которые кодируются символом 1, и непростые, кодируемые символом 0). Описаны также эксперименты, показывающие, что предсказывающие автоматы, полученные путем моделирования эволюции, могут использоваться при распознавании образов, для диагностики и управления неизвестными объектами.
выпадения герба) или нестационарных случайных последовательностей (например, предсказание последовательности 0,1,1,1,0,1,0,1,0,0,0,1, … , полученной в результате классификации чисел натурального ряда 0,1,2,3,4,5,6,7,8,9,10,11, … на простые, которые кодируются символом 1, и непростые, кодируемые символом 0). Описаны также эксперименты, показывающие, что предсказывающие автоматы, полученные путем моделирования эволюции, могут использоваться при распознавании образов, для диагностики и управления неизвестными объектами.
Синтез прогнозирующих автоматов средствами эволюционного моделирования можно рассматривать и как синтез предсказывающих фильтров, поиск параметров которых ведутся методом случайного поиска. Известно, что эволюционирующие фильтры обычно имеют детерминированную часть, связанную с анализом причин и следствий, которую можно рассчитать, и индетерминированную часть – случайный корректор. Разумное сочетание детерминированных и индетерминированных вычислений позволяет существенно повысить эффективность алгоритмов эволюционного моделирования и расширить область их применения. В частности, это позволяет во многих случаях применять и более гибкий подход к эволюционному процессу, который дает возможность использовать конечные автоматы или непрерывные регуляторы в контурах управления объектов, находящихся в изменяющейся внешней среде. Он предполагает иерархическую 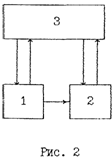 двухуровневую процедуру, блок-схема которой приведена на рис. 2, где 1 – алгоритм структурной адаптации; 2 – алгоритм использования; 3 – алгоритм параметрической адаптации.
двухуровневую процедуру, блок-схема которой приведена на рис. 2, где 1 – алгоритм структурной адаптации; 2 – алгоритм использования; 3 – алгоритм параметрической адаптации.
На первом уровне постоянно протекают два процесса: процесс использования одного из к хранящихся в памяти синтезированных регуляторов в контуре управления и процесс синтеза множества моделей регуляторов. При ухудшении качества работы функционирующего регулятора на i-м этапе он заменяется одним из синтезированных на (i-1)-м этапе регулятором либо одним из регуляторов, хранящихся в памяти. На (i+1)-м этапе функционирует новая модель регулятора и опять выполняется синтез множества моделей регуляторов. Поскольку синтез эффективной структуры регулятора во многом зависит от таких параметров эволюционного процесса, как список возможных мутаций адаптируемых моделей, вероятности появления тех или иных режимов изменения, длины предыстории или объема используемой памяти на этапе адаптации и других параметров, то необходим алгоритм, который бы адаптировал параметры эволюционного процесса структурной адаптации моделей регуляторов. Такая адаптация выполняется с помощью алгоритма параметрической адаптации, который фактически адаптирует алгоритмы случайного поиска моделей регуляторов по поступающей из внешней среды информации и результатам функционирования регуляторов в контуре управления.
Адаптация случайного поиска существенно повышает эффективность алгоритмов эволюционного синтеза моделей, однако она не может полностью компенсировать отсутствие комплексного сочетания детерминированных и индетерминированных вычислений. Отсутствие такого сочетания приводит к тому, что там, где были бы эффективны простые детерминированные процедуры (например, модель находится на склонах «холма» или «пика» с глобальным экстремумом в многоэкстремальном пространстве возможных моделей и для получения лучшего решения необходимо только оптимизировать один-два параметра модели) применяется трудоемкий случайный поиск (при синтезе конечных автоматов генерируются автоматы во всем пространстве возможных решений, а не только на склонах «холма» или «пика», на которых находится лучший синтезированный на данный момент автомат). Это часто чрезмерно увеличивает время счета, а следовательно, и ограничивает область применения эволюционного моделирования.
Для решения задач синтеза или адаптации автоматов в случае предельной априорной неопределенности лучше вводить универсальные алгебры a(m,d), отражающие специфику решаемой задачи. Здесь M – множество возможных переходов 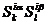 конечных автоматов
конечных автоматов 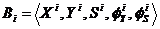 из состояния
из состояния 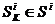 в состояние
в состояние 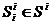 при заданных конечных входном Xi и выходном Yi алфавитах (
при заданных конечных входном Xi и выходном Yi алфавитах (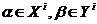 ); i, i =
); i, i = 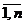 , – индекс, указывающий на принадлежность к i-му автомату; Si – конечное множество состояний;
, – индекс, указывающий на принадлежность к i-му автомату; Si – конечное множество состояний; 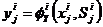 – функция выходов;
– функция выходов; 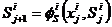 – функция переходов;
– функция переходов; 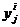 ,
, 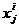 и
и 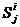 – соответственно выходной символ, входной символ и состояние i-го конечного автомата Bi в момент времени tj, j=i, 2, ... ; D – множество операций алгебры, которая должна содержать операции, позволяющие наиболее просто решать задачу синтеза или адаптации автомата из некоторого множества
– соответственно выходной символ, входной символ и состояние i-го конечного автомата Bi в момент времени tj, j=i, 2, ... ; D – множество операций алгебры, которая должна содержать операции, позволяющие наиболее просто решать задачу синтеза или адаптации автомата из некоторого множества 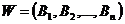 исходных автоматов при заданном множестве I исходных данных.
исходных автоматов при заданном множестве I исходных данных.
При заданной последовательности входных сигналов 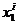 ,
, 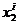 , … ,
, … , 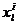 выходные сигналы (реакции)
выходные сигналы (реакции) 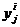 ,
, 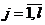 , объектов Bi,
, объектов Bi, 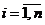 , переводят наборы (I, B1, B2, … ,Bn) в информационную матрицу
, переводят наборы (I, B1, B2, … ,Bn) в информационную матрицу 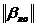 ,
, 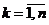 ,
, 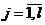 , где
, где 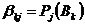 ,
, 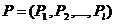 – множество предикатов, определенных на множестве автоматов,
– множество предикатов, определенных на множестве автоматов, 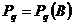 ,
, 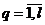 . Строка (
. Строка (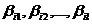 ) информационной матрицы )
) информационной матрицы ) 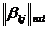 ; является информационным вектором автомата Bi и составлена из элементов 0 и 1, т. е. из значений предикатов, вычисленных при функционировании автомата. Если все элементы строки являются единицами, то автомат называется корректным для решаемой задачи Z.
; является информационным вектором автомата Bi и составлена из элементов 0 и 1, т. е. из значений предикатов, вычисленных при функционировании автомата. Если все элементы строки являются единицами, то автомат называется корректным для решаемой задачи Z.
На множестве значений выходных функций вводятся метрики 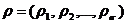 , с помощью которых путем введения множества
, с помощью которых путем введения множества 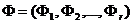 функционалов на множестве значений выходных функций автоматов, оценивается отклонение функционирования некорректных автоматов от функционирования корректных. Если при функционировании автомата выполняются условия
функционалов на множестве значений выходных функций автоматов, оценивается отклонение функционирования некорректных автоматов от функционирования корректных. Если при функционировании автомата выполняются условия 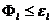 ,
, 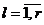 , где
, где 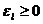 – некоторые наперед заданные величины, то он называется автоматом с заданной мерой некорректности функционирования (при
– некоторые наперед заданные величины, то он называется автоматом с заданной мерой некорректности функционирования (при 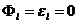 ,
, 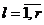 имеем корректный автомат). При рациональном выборе множеств D, Р,
имеем корректный автомат). При рациональном выборе множеств D, Р, 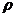 ,
, 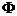 обычно существуют признаки возможности или невозможности синтеза корректных автоматов или автоматов с заданной мерой некорректности функционирования из заданного множества w исходных объектов и множества I исходных данных. При наличии указанных признаков задача получения объекта для решения некоторой задачи Z выполняется следующим образом.
обычно существуют признаки возможности или невозможности синтеза корректных автоматов или автоматов с заданной мерой некорректности функционирования из заданного множества w исходных объектов и множества I исходных данных. При наличии указанных признаков задача получения объекта для решения некоторой задачи Z выполняется следующим образом.
На первом этапе стандартным методом получается множество W* автоматов, из которых по указанным признакам для данной задачи Z из множества W* с помощью множества операций D алгебры A(M, D) может быть получен корректный автомат (или автомат с заданной мерой некорректности). На втором этапе выполняется композиция или преобразование полученных объектов и для последующей работы отбирается подмножество лучших (в смысле заданного множества функционалов) автоматов, такое, что для данной задачи Z из них может быть получен корректный автомат (автомат с заданной мерой некорректности). Затем выполняется композиция или преобразование вновь полученных автоматов и так далее - до тех пор, пока не будет получен один или подмножество автоматов, каждый из которых решает заданную задачу Z. При решении задачи адаптации автомата в исходное множество W* включается и ранее функционировавший автомат.
Успешный синтез конечного автомата, а также затраты на его осуществление как при использовании алгебраического подхода, так и классических алгоритмов эволюционного моделирования, во многом зависят и от удачного определения исходного множества автоматов B*, из которых для данной задачи с помощью выбранного алгоритма можно синтезировать корректный (или с заданной мерой некорректности функционирования) автомат. В случае больших обучающих последовательностей и использования K-значных (K >> 2) входных и выходных алфавитов этап получения исходного множества автоматов может быть чрезвычайно трудоемким в связи с тем, что при его выполнении будет синтезировано множество бесперспективных частных описаний различной сложности, которые затем будут опробованы на обучающих выборках и отброшены как работающие неудовлетворительно. В то же время простой предварительный анализ исходных данных может существенно сократить необходимые переборы частных описаний. Действительно, если, например, имеется обучающая последовательность, содержащая группу из j символов 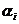 и m пар символов
и m пар символов 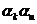 (
(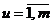 ),
),
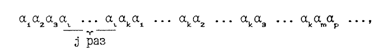
и требуется синтезировать автомат, который безошибочно предсказывает все символы обучающей последовательности, то такой автомат должен иметь число состояний, которое определяется большим из двух чисел j и m, и, следовательно, на первом ряду селекции в множество B* необходимо сразу вводить автоматы с N = max(j,m) состояниями, не рассматривая более простые автоматы. Для определения числа m необходим просмотр всех пар следующих друг за другом входных символов, а для определения числа j – анализ групп входных символов, каждая из которых содержит j символов. В общем случае анализ входной последовательности можно представить следующим образом. Имеется входная последовательность I={i1 ,i2 ,...,in} из алфавита А = {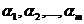 } входных символов и имеется множество предикатов Р = {Р1, Р2, ..., Рl}. которые характеризуют неоднородность участия символов алфавита А в образовании различных комбинаций символов во входной последовательности. Наличие или отсутствие интересующего нас свойства Rq входной последовательности будем описывать предикатом Рq, аргументами которого являются группы или отдельные символы входного алфавита А:
} входных символов и имеется множество предикатов Р = {Р1, Р2, ..., Рl}. которые характеризуют неоднородность участия символов алфавита А в образовании различных комбинаций символов во входной последовательности. Наличие или отсутствие интересующего нас свойства Rq входной последовательности будем описывать предикатом Рq, аргументами которого являются группы или отдельные символы входного алфавита А:

Рассмотрим, например, неоднородность участия в образовании входной последовательности символов 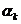 и
и 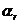 . Искомую неоднородность можно характеризовать числами nk, nr вхождения каждого из символов во входную последовательность I и представить в виде диагональной матрицы F1, в которой диагональные элементы aii = ni,
. Искомую неоднородность можно характеризовать числами nk, nr вхождения каждого из символов во входную последовательность I и представить в виде диагональной матрицы F1, в которой диагональные элементы aii = ni, 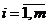 . Максимальное число
. Максимальное число 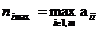 на диагонали матрицы F1 дает грубую оценку максимально необходимого числа состояний корректного конечного автомата, безошибочно предсказывающего по текущему символу следующий символ входной последовательности.
на диагонали матрицы F1 дает грубую оценку максимально необходимого числа состояний корректного конечного автомата, безошибочно предсказывающего по текущему символу следующий символ входной последовательности.
Диагональные элементы матрицы F1 можно использовать и для грубой оценки числа nc состояний автоматов с заданной мерой некорректности. Например, если задано, что число ошибок предсказания автомата не должно превышать NЭ, то используя соотношение
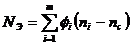 (1)
(1)
где
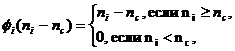
можно получить примерное значение числа nc.
Видимо, оценки числа состояний корректных автоматов или автоматов с заданной мерой некорректности будут более точными, если наряду с числами nj, 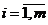 , определять число пар входных символов, содержащих один из символов
, определять число пар входных символов, содержащих один из символов 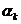 или
или 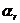 , а также число упорядоченных пар
, а также число упорядоченных пар 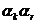 или
или 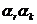 . В общем случае, когда индексы k и г изменяются от единицы до m, можно построить частотную матрицу F2 вида
. В общем случае, когда индексы k и г изменяются от единицы до m, можно построить частотную матрицу F2 вида
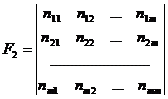 , (2)
, (2)
где nij – число упорядоченных пар 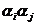 символов во входной последовательности.
символов во входной последовательности.
Вместо матрицы (2) иногда удобнее рассматривать матрицу F2p из значений предикатов
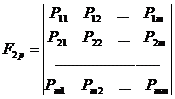 , (3)
, (3)
где
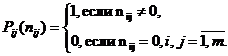 (4)
(4)
Наибольшее число nmax отличных от нуля элементов в строке F2pi матрицы (3) или в соответствующей строке матрицы F2i (2) определяет нижнюю границу числа состояний конечного автомата, необходимых для правильного предсказания всех пар символов, в том числе и всех пар 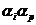 (
(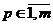 ) с наиболее разнообразно входящим в последовательность I символом
) с наиболее разнообразно входящим в последовательность I символом 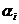 . Минимально необходимое для правильного предсказания всех символов число состояний автомата зависит не только от Nmax, но и от величины максимального элемента
. Минимально необходимое для правильного предсказания всех символов число состояний автомата зависит не только от Nmax, но и от величины максимального элемента 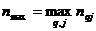 матрицы F2, поскольку в худших случаях (например, все пары элементов
матрицы F2, поскольку в худших случаях (например, все пары элементов 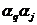 следуют одна за другой) для безошибочного предсказания необходимо nmax состояний конечного автомата. Однако в других случаях, например, при циклической входной последовательности, когда группы пар символов
следуют одна за другой) для безошибочного предсказания необходимо nmax состояний конечного автомата. Однако в других случаях, например, при циклической входной последовательности, когда группы пар символов 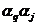 разделены одинаковыми подпоследовательностями символов, величина максимального элемента матрицы может существенно превышать минимально необходимое число состояний конечного автомата, требуемое для безошибочного воспроизведения входной последовательности. Такая неопределенность в оценке необходимого числа состояний конечного автомата требует дальнейшего дополнения характеристик входной последовательности и рассмотрения неоднородности участия троек, четверок, ..., L-ек символов в образовании свойств входной последовательности. Рассмотрим L-мерную матрицу:
разделены одинаковыми подпоследовательностями символов, величина максимального элемента матрицы может существенно превышать минимально необходимое число состояний конечного автомата, требуемое для безошибочного воспроизведения входной последовательности. Такая неопределенность в оценке необходимого числа состояний конечного автомата требует дальнейшего дополнения характеристик входной последовательности и рассмотрения неоднородности участия троек, четверок, ..., L-ек символов в образовании свойств входной последовательности. Рассмотрим L-мерную матрицу:
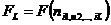 , i1, i2, … , iL=1, m.
, i1, i2, … , iL=1, m.
Места на каждой стороне матрицы пронумеруем числами от единицы до m. Каждому числу 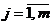 поставим в соответствие символ
поставим в соответствие символ 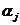 алфавита A, а каждому элементу
алфавита A, а каждому элементу 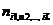 - число упорядоченных L-ек символов, в которые входят символы алфавита, соответствующие номерам индексов i1, i2, … , iL
- число упорядоченных L-ек символов, в которые входят символы алфавита, соответствующие номерам индексов i1, i2, … , iL 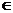
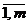 выбранного элемента
выбранного элемента 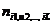 матрицы. Построенную таким образом матрицу называют L-мерной частотной матрицей входной последовательности.
матрицы. Построенную таким образом матрицу называют L-мерной частотной матрицей входной последовательности.
Наличие L-мерной частотной матрицы FL позволяет уточнить нижнюю оценку необходимого числа состояний конечных автоматов. Например, в случае, когда синтезируется автомат, который должен точно предсказывать все символы обучающей последовательности, наличие хотя бы одного отличного от нуля элемента 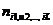 , когда i1 = i2 = … = iL и
, когда i1 = i2 = … = iL и 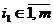 , указывает, что минимально необходимое число состояний конечного автомата в общем случае не меньше L.
, указывает, что минимально необходимое число состояний конечного автомата в общем случае не меньше L.
Вместо L-мерных матриц можно использовать более наглядные двумерные матрицы, пронумеровав их столбцы и строки таким образом, чтобы в них в удобной форме были перечислены все элемент L-мерной матрицы.
Отметим, что по аналогии с матрицей (3) вводятся многомерные или соответствующие им двумерные матрицы предикатов для L-ек символов .
Частотные матрицы целесообразно использовать и при синтезе конечных автоматов с заданной мерой некорректности функционирования .
Пример 1. Пусть задана последовательность из 22 символов 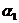
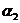
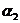
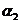
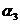
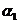
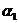
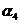
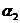
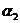
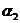
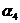
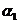
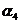
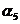
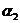
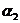
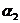
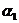
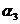
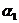
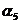 . Необходимо синтезировать конечный автомат, точно предсказывающий по текущему символу следующий символ входной последовательности.
. Необходимо синтезировать конечный автомат, точно предсказывающий по текущему символу следующий символ входной последовательности.
Матрицы F1, F2 в этом случае имеют вид
 ,
, 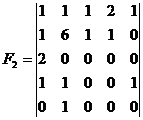 .
.
Максимальный элемент матрицы F1 указывает на то, что число состояний конечного автомата не превышает девяти, а из пяти ненулевых элементов первой строки матрицы F2 следует, что автомат, безошибочно предсказывающий всю входную последовательность, не может иметь менее пяти состояний. Из величины максимального элемента второй строки матрицы F2 и общего числа символов 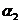 (максимальный элемент матрицы F1 ) без анализа троек символов не удается снизить верхнюю границу числа состояний конечного автомата. Анализ троек символов с помощью матрицы
(максимальный элемент матрицы F1 ) без анализа троек символов не удается снизить верхнюю границу числа состояний конечного автомата. Анализ троек символов с помощью матрицы
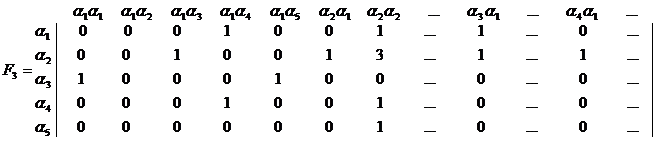
показывает, что имеется три тройки символов 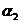 ,
,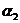 ,
,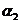 , отделенные друг от друга различными группами символов (все тройки символов
, отделенные друг от друга различными группами символов (все тройки символов 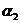 ,
,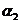 ,
,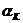 (k = 1, 3, 4) различны). Поэтому число состояний автомата, безошибочно предсказывающего всю входную последовательность, не может быть меньше
(k = 1, 3, 4) различны). Поэтому число состояний автомата, безошибочно предсказывающего всю входную последовательность, не может быть меньше
n = ki n *,
где ki - число групп символов 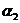 ,
,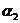 ,
,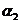 (максимальный элемент матрицы F3); n* - число состояний конечного автомата, необходимых для безошибочного предсказания последовательности
(максимальный элемент матрицы F3); n* - число состояний конечного автомата, необходимых для безошибочного предсказания последовательности 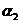 ,
,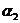 ,
,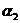 ,
,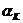 . Отсюда следует, что n = 9 и что автомат должен состоять из трех подавтоматов, правильно предсказывающих соответственно подпоследовательности символов
. Отсюда следует, что n = 9 и что автомат должен состоять из трех подавтоматов, правильно предсказывающих соответственно подпоследовательности символов 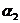 ,
,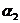 ,
,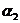 ,
,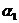 ;
; 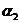 ,
,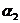 ,
,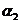 ,
,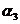 ;
; 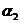 ,
,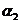 ,
,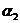 ,
,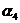 . Такая информация на несколько порядков сокращает объем необходимых вычислений.
. Такая информация на несколько порядков сокращает объем необходимых вычислений.
Пример 2. Пусть задана входная последовательность примера 1 и требуется оценить число N ошибочных предсказаний автомата с пятью состояниями.
Из соотношения (1) и матрицы F1 примера 1 следует, что
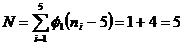 .
.
Анализ матрицы F2 показывает, что автомат с пятью состояниями, предсказывая вторые элементы пар символов 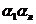 (
(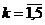 ) может не допустить ни одной ошибки, т. е. верхняя оценка числа неправильных предсказаний, как-будто, может быть уменьшена на единицу. Однако более глубокий анализ - анализ матрицы F3 показывает, что тройки символов
) может не допустить ни одной ошибки, т. е. верхняя оценка числа неправильных предсказаний, как-будто, может быть уменьшена на единицу. Однако более глубокий анализ - анализ матрицы F3 показывает, что тройки символов 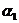 ,
,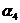 ,
,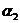 и
и 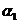 ,
,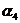 ,
,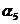 можно правильно предсказать только в том случае, когда символ
можно правильно предсказать только в том случае, когда символ 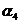 в них предсказывается разными состояниями автомата. Это свидетельствует о том, что величина оценки по первой строке матрицы F1 числа ошибок с помощью соотношения (1) не может быть уменьшена. Совместный анализ матриц F2 и F3, проведенный в примере 1, показывает, что девять состояний автомата, безошибочно предсказывающего все символы входной последовательности, обусловливаются наличием трех групп символов
в них предсказывается разными состояниями автомата. Это свидетельствует о том, что величина оценки по первой строке матрицы F1 числа ошибок с помощью соотношения (1) не может быть уменьшена. Совместный анализ матриц F2 и F3, проведенный в примере 1, показывает, что девять состояний автомата, безошибочно предсказывающего все символы входной последовательности, обусловливаются наличием трех групп символов 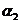 ,
,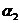 ,
,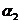 ,
,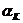 (k = 1, 3, 4), для правильного предсказания каждой из которых требуется три состояния конечного автомата. Следовательно, автомат с пятью состояниями на подпоследовательностях, начинающихся с символа
(k = 1, 3, 4), для правильного предсказания каждой из которых требуется три состояния конечного автомата. Следовательно, автомат с пятью состояниями на подпоследовательностях, начинающихся с символа 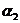 , должен делать не менее двух ошибок. Поскольку величина оценки числа ошибок по третьей - пятой строкам матрицы F1 с помощью соотношения (1) имеет нулевое значение, то весьма вероятно существование автомата с пятью состояниями, делающего всего три неправильных предсказания на заданной входной последовательности. Автомат, имеющий пять состояний и делающий всего три неправильных предсказания, действительно удается синтезировать.
, должен делать не менее двух ошибок. Поскольку величина оценки числа ошибок по третьей - пятой строкам матрицы F1 с помощью соотношения (1) имеет нулевое значение, то весьма вероятно существование автомата с пятью состояниями, делающего всего три неправильных предсказания на заданной входной последовательности. Автомат, имеющий пять состояний и делающий всего три неправильных предсказания, действительно удается синтезировать.
Частотный метод анализа необходимо дополнять хотя бы простейшими элементами анализа во временной области. Дело в том, что важно не только наличие, например L-ки 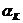 , … ,
, … ,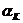 символов , но
символов , но 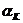 и где эта L-ка расположена во входной последовательности: если в начале или в середине входной последовательности, то для безошибочного предсказания всех символов
и где эта L-ка расположена во входной последовательности: если в начале или в середине входной последовательности, то для безошибочного предсказания всех символов 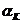 и следующего за ними символа необходимо L состояний конечного автомата, а если в конце последовательности, то безошибочное предсказание может быть выполнено одним состоянием конечного автомата.
и следующего за ними символа необходимо L состояний конечного автомата, а если в конце последовательности, то безошибочное предсказание может быть выполнено одним состоянием конечного автомата.
Другой факт из пространственно-временного анализа, позволяющий часто во много раз сократить объем необходимых вычислений. Если входная последовательность имеет длину N символов и выполняется синтез предсказывающего автомата, то теоретически нет смысла рассматривать конечные автоматы с более чем (N – 1) переходами, а практически - более чем с (0,5 - 0,7) (N - 1) переходами. Следовательно, при алгебраической форме представления автоматов необходимо оценивать только автоматы, содержащие не более (0,5 -0,7) (N - 1) одночленов, что ведет к резкому сокращению числа возможных автоматов-претендентов.
3. РАБОТА С ПРОГРАММОЙ ЭВОЛЮЦИОННОГО СИНТЕЗА КОНЕЧНЫХ АВТОМАТОВ
Программа выполнена на языке Turbo Pascal 7.0. При запуске программы на выполнение появляется меню:
1......Пошаговый режим Нет
2......Случайные мутации Да
3......Задание вероятностей мутаций Нет
4......Задание входной последовательности Нет
5......Периодический запрос подтверждения Нет
6......Задание исходного автомата Нет
Enter..Начало генерации конечного автомата
Esс Выход
Для изменения заданного в меню режима работы программы необходимо нажать на клавиатуре цифру соответствующего режима - это меняет содержимое правого столбца меню с «Нет» на «Да» или наоборот.
Пошаговый режим работы программы предусматривает вывод на экран полученного автомата после каждой мутации. Для его задания необходимо ввести «I», после чего в первой строке меню появится «Да» вместо «Нет». Режим может отменяться в процессе выполнения программы.
В программе предусмотрено пять типов мутаций конечных автоматов: добавление состояния, удаление состояния, изменение ребер автоматов, изменение выходных символов связей автоматов, изменение начального состояния. Вероятность применения каждого вида мутаций может быть определена пользователем в режиме «Задание вероятностей мутаций», в противном случае используются значения вероятностей, заданных в программе (их численные значения выводятся на экран в рассматриваемом режиме).
В четвертом режиме работы программы может быть задана необходимая входная последовательность, параметры которой (длина и алфавит) задаются соответственно константами программы ValLen и Radix. Константа Radix задает алфавит посредством определения основания системы счисления входной последовательности. Например, при Radix = 2 входной алфавит состоит из символов {0, 1}, а при Radix = К - из символов (0, 1, ..., К – 1).
В пятом режиме работы может быть задано число мутаций, после которого программа запрашивает о целесообразности дальнейшего поиска конечного автомата:
5
1......Пошаговый режим Нет
5......Периодически запрашивать подтверждение Да
Esc Выход
Enter
Введите число мутаций, после которого запрашивать
подтверждение _
1000 Enter
Please wait ...
Произошло 1000 мутаций. Продолжить? (Y/N)
Y
Произошло 2000 мутаций. Продолжить? (Y/N)
N
После этого на экране появляется лучший конечный автомат, полученный после 2000 мутаций, входная и выходная последовательности и процент правильных предсказаний символов входной последовательности.
Режим 6 используется в тех случаях, когда необходимо задать исходный автомат. Для начала работы этого режима необходимо ввести «6», после чего в шестой строке меню вместо «Нет» появится «Да», а затем - Enter - и на экране появится меню
1...Добавить состояние и выходы из него
2...Удалить последнее состояние
3...Перебросить связь на другое состояние
4...Изменить выходной символ связи
5...Принять другое состояние в качестве начального
ESC.Принять этот автомат за исходный
Пусть после двукратного нажатия «1» получим на экране автомат
1 2
1 0/1 -
1/0
2 1/0 0/0
Начальное состояние: 1
Для демонстрации работы программы в режимах 3, 4 и 5 предположим, что необходимо заменить связь 1/0 из состояния 1 в состояние 1 на связь 1/1 из состояния 1 в состояние 2 и изменить при этом начальное состояние автомата с первого на второе. В начале изменим начальное состояние, а затем - выходной символ:
5
Введите номер начального состояния _
2 Enter
4
Изменить выходной символ связи:
из 1 Enter
в 1 Enter
номер связи (0-1) _
1 Enter
выходной символ: 1 Enter
Все введенное Вами правильно? (Y/N)
Y
Если информация введена неправильно, то после ввода «N» программа предоставляет возможность повторить ввод. Для изменения конечного состояния связи 1/1 в первой вершине автомата используем режим 3:
3
Связь:
из 1 Enter
в 1 Enter
номер (0-1) 1 Enter
Перебросить в 2 Enter
Все введенное Вами правильно? (y/n)
Y
В результате на экране получим автомат:
1 2
1 0/1 1/1
2 1/0 0/0
Начальное состояние: 2
Перед началом работы программы при необходимости могут бить изменены основные константы программы:
MaxState - максимально возможное количество состояний конечного автомата, исходное значение - 10;
Radix - основание системы счисления входной последовательности, исходное значение - 2;
IdealKoef - коэффициент, задающий процент правильных предсказаний на входной последовательности синтезируемого автомата, исходное значение - 0,9;
ValLen - длина входной последовательности, исходное значение - 10.
Программа:
Program Evoi;
uses Crt;
{
MaxState - максимально возможное число состояний автомата
Radix - основание системы счисления для входной последовательноcти
MaxNum - наибольшая цифра заданной системы счисления
Illegal - значение веса, свидетельствующее о том, что связь,
имеющая такой вес, свободна (например, в двоичной
системе это значение 2/2)
IdealKoef - заданный процент правильных предсказаний на обучающей
последовательности синтезируемого автомата
MaxMut - число разновидностей мутаций, в данном случае их 5:
1) добавить состояние (AddState);
2) Удалить состояние (DelState);
3) Перебросить связь на другое состояние, возможно,
изменив ее выходной сигнал (DelAdj);
4) Изменить выходной сигнал связи (ChangeWgt);
5) Принять другое состояние в качестве входа
(Change First).
ValLen - длина входной последовательности
Steps - количество мутаций, после которого надо запросить
подтверждение на продолжение работы программы
VerErr - Ошибка, допустимая при вводе вероятностей
(максимальное отклонение суммы вероятностей от 1)}
Const
MaxState=10;
Radix=2;
MaxNum=Radix-1;
Illegal=Radix shl 8 + Radix;
IdealKoef=0.9;
MaxMut=5;
ValLen=10;
F8=#66;
F9=#67;
Esc=#27;
Enter=#13;
Steps:longint=500;
VerErr=0.01;
{ -------- ТИПЫ -------
Alt : алфавит, используемый конечным автоматом
Diap,index: диапазон значений счетчика состояний }
type
Alf=0..MaxNum;
Diap=0..MaxState;
Index=1..MaxState;
MutType=1..MaxMut;
ValLenType=0..ValLen;
VerType=array [MutType] of real;
ValType=array [ValLenType] of Alf;
KeySet=set of char;
{ Еще константы ------
Delta : константа для изменения вероятности мутаций
Ver : вероятности мутаций }
const
Delta=1/5/MaxMut;
Ver:VerType=(
{AddState} 1/MaxMut-Delta,
{DelState} 1/MaxMut+Delta,
{DelAdj } 1/MaxMut,
{ChangeWg t} 1/MaxMut,
{Change?irst}1/MaxMut);
Keys12:KeySet=['1','2'];
Keys01:KeySet=['0','1'];
KeysYN:KeySet=['y', 'n', 'Y', 'N' ];
Keys12345Esc:KeySet=['1','2','3','4','5',Esc];
Keys12345Ent:KeySet=['1','2','3','4','5',Enter];
Keys1_6EE:KeySet=['1','2','3','4','5','6',Enter,Esc];
{ ----- Переменные ------
Vers : внутренняя для вычисления вероятностей ValsOut: выходная последовательность }
var
Vers:VerType;
ValsOut:ValType;
{ ------- Основная часть ------
WgtRec : описывает связь: Win- вход, Wout- выход
GrafRec: структура данных, представляющая граф
Поля:
First: вход графа
States: матрица переходов. Ее элементы определяют число связей,
идущих из состояния X в состояние у (0 означает, что нет ни одной связи.
Wgt: матрица весов. Ее элементы типа WgtRec определяют вес каждой из связей x->Y (например, 1/0, о/О и т.д.)
CurStates: количество состояний
OurStt: текущее состояние
Koef: коэффициент правильности работы
Graf : собственно граф
Поля:
Body: граф, с которым производятся все операции
GrafError: состояние после выполненной операции:
ошибка была (true) или нет (false)
Avt : конечный автомат
Поля:
Best: лучший автомат, используемый для селекции
Trace флаг пошагового режима (true- включен)
Value входная последовательность
NMuts количество мутаций }
type
WgtRec=
Record
Win,Wout:Alf;
end;
GrafRec=
Object
First: Diap;
States: array [Index,Index] of Diap; { матрица переходов } { показывает, сколько связей }
Wgt: array [Alf,Index,Index] of WgtRec; { матрица весов }
CurStates: Diap; { max. состояние }
CurStt : Diap; { текущее состояние.}
Koef : real;
end;
Graf =
Object
Body:GrafRec;
GrafError:boolean;
Constructor Init;
Destructor Done;
Procedure AddAdJ (from,_to:Index;W:WgtRec);virtual;
Procedure DelAdj (from,_to,NewAdj:Index;which:Alf);virtual;
Function NWgt (from,_to:Index):Diap; { КОЛ-ВО связей }
Procedure ChangeWgt (from,_to:Index;Which:Alf;NewWgt:WgtRec);
Procedure AddState;virtual;
Procedure DelState;virtual;
Procedure Draw;virtual;
end;
Avt=
object(Graf)
Best:GrafRec;
Trace: boolean;
Value: ValType;
NMuts: longint;
Constructor Init;
Procedure Config;virtual;
Procedure Advlnit;virtual;
Procedure DoTheBest;
Procedure Draw;virtual;
Function MutNum:MutType; { как мутировать }
Procedure Mutation;
Procedure Store;
Procedure Restore;
Function IsBest :boolean;
Procedure GetKoef;
Procedure AddState;virtual; { добавить состояние и выходы из него }
Procedure DelState;virtual;
Procedure DelAdj (from,_to,NewAdj:Index;Which:Alf);virtual;
{ переброска связи в другое состояние }
Procedure _DelAdj;
Procedure AddAdj (from,_to:Index;W:WgtRec);virtual;
Procedure _ChangeWgt;
Procedure ChangeWgt (from,_to:Index;Which:Alf;NewWgt:WgtRec);
Procedure ChangeFirst (NewFirst: Index);
Procedure _ChangeFirst;
Procedure DelAdj_ask;
Procedure ChangeWgt_ask;
Procedure ChangeFirst_ask;
end; { A V Т }
{--------- Глобальные функции -------
***** GetVal ****
Выдает символ входной последовательности с номером t }
Function GetVal(t:ValLenType):Alf;
var
x:longint;
Function f(p:longint):longint;
{ функция, задающая входную последовательность;
в принципе может быть произвольной }
var
ff:real;
Begin
ff:= (sqrt (p*4));
f:=abs (round(ff));
End; { GetVal.f }
Begin
x:=f(t);
GetVal:=x mod Radix;
End; { GetYal }
{ ***** GetKey ****
Читает символ из множества ks с клавиатуры }
Function GetKey (var ks :KeySet;echo:boolean):char;
var
c:char;
Begin
Repeat
c:=Readkey
until c in ks;
If echo then Write (c,' ');
GetKey:=c;
End; { GetKey }
{ **** GetNum *****
Читает с клавиатуры число, пока оно не будет введено правильно
Min, Max: диапазон значений вводимого числа }
Function GetNum (Min, Max: longint): longint;
var
s:string;
ec:integer;
n:longint;
Begin
Repeat
Readln (s);
Val (s,n,ec);
until (ec=0) and (n<=Max) and (n>=Min);
GetNum:=n;
End; { GetNum }
{ ***** GetReal ***** To же самое, но для вещественных чисел }
Function GetReal (Min,Max:real):real;
var
s:string;
ec:integer;
n:real;
Begin
Repeat
Readln (s);
Val (s,n,ec);
until (ec=0) and (n<=Max+1e-10) and (n>=Min-1e-10);
GetReal:=n;
End; { GetReal }
{ ***** confirm ***** Запрашивает подтверждение у пользователя Возврат:
true, если ответ ДА
false- если НЕТ }
Function Confirm:boolean;
Begin
Writeln (#13#10'Bce введенное Вами правильно? (Y/N)');
Confirm:=UpCase(GetKey (KeysYN,false))='Y';
End; { Confirm }
{ ------- Методы графа ----------
**** init ****
обнуляет все, что можно; кроме того, заносит в матрицу
весов значения, свидетельствующие о пустоте связей (Illegal) }
Constructor Graf.Init;
begin
TextMode(CO80);
ClrScr;
GrafError:=false;
With Body do
begin
First:=0;
CurStates:=0;
CurStt:=0;
Koef:=0.0;
FillChar (Wgt,SizeOf(Wgt),byte(Radix));
FillChar (States,SizeOf(States),0);
end;
End; { Graf.Init }
{ *** РППР ****
Просто подождать нажатия клавиши }
Destructor Graf.Done;
Begin
GotoXY (28,25);
Write ('Нажмите любую клавишу');
ReadKey;
End; { Graf.Done }
{ **** DelAdj ****
Удалить связь с номером which из состояния
from в состояние
_to и сдвинуть остальные
Переменные:
i : счетчик
w : вес
w1: для обхода Range check error при стирании связи }
Procedure Graf.DelAdj(from, _to, NewAdj: Index; which: Alf);
var
i:-1..MaxNum;
w:WgtRec;
w1:word absolute w;
Begin
GrafError:=false;
If (from>Body.CurStates)or(_to>Body.CurStates )or(NWgt( from,_to)=0) then
begin
GrafError:= true;
Exit;
end;
w1:=Illegal;
With Body do
begin
Dec(States [from,_to]);
For i:=which to States [from,_to]-1 do
Wgt [i,from,_to]:=Wgt [i+1,from,_to];
Wgt[States [from,_to],from,_to]:=w;
end;
End; { Graf.DelAdj }
{ **** AddAdj *****
Добавление связи из from в _to с весом w }
Procedure Graf.AddAdj (from,_to:Index;W:WgtRec);
var
i,N:Diap;
j:-1..MaxState;
Begin
GrafError:= false;
N:=NWgt (from,_to);
With Body do
begin
If (N=Radix)or(from>CurStates)or(_to>CurStates) then
begin
GrafError:=true;
Exit;
end;
Inc (States [from,_to]);
Wgt [N,from,_to]:=W;
end;
End; { Graf.AddAdj }
{ *** NWgt ****
Количество связей from -> _to }
Function Graf.NWgt (from,_to:Index):Diap;
Begin
GrafError:=false;
If (from>Body.CurStates)or(_to>Body.CurStates) then
begin
GrafError:=true;
NWgt:=0;
Exit;
end;
NWgt:=Body.States [from,_to];
End; { Graf.NWgt }
{ *** changeWgt ****
Изменить вес связи from->_to с номером Which на NewWgt }
Procedure Graf.ChangeWgt (from,_to:Index;Which:Alf;NewWgt:WgtRec);
Begin
GrafError:=false;
If (from>Body.CurStates) or (_to>Body.CurStates)or (NWgt(from,_to)<Which) then
begin
GrafError:= true;
Exit;
end;
Body.Wgt [Which,from,_to]:=NewWgt;
End; { Graf.ChangeWgt }
{ **** AddState **** Добавление состояния }
Procedure Graf.AddState;
Begin
GrafError:=false;
With Body do
begin
If CurStates=MaxState then
begin
GrafError:=true;
Exit;
end;
Inc(CurStates);
FillChar (States[CurStates,1],MaxState,0);
end;
End; { Graf.AddState }
{ **** DelState ****
Удаление последнего состояния. Переменные - аналогично Graf.DelAdj}
Procedure Graf.DelState;
var
w:WgtRec;
w1:word absolute w;
i:Diap;
J:Alf;
Begin
GrafError := false;
With Body do
begin
If CurStates<=1 then
begin
GrafError:=true;
Exit;
end;
w1 := Illegal;
For i:=1 to CurStates do
For j:=0 to MaxNum do
Wgt[j,CurStates,i]:=w;
If First=CurStates then Dec (First);
Dec(CurStates);
end;
End; { Graf.DelState }
{ **** Draw **** Изображение графа на экране }
Procedure Graf.Draw;
var
i,j:Diap;
k:Alf;
x,xx,y:byte;
Begin
ClrScr;
With Body do
begin
Write (' ');
For i:=1 to CurStates do Write (i:2,' ');
Writeln(i:2,' ');
For i:=1 to CurStates do
begin
Write (i:2,' ');
For j:=1 to CurStates do
begin
y:=WhereY;
x:=WhereX;
If States [i,j]=0 then
begin
Write ('--- ');
xx:=WhereX;
end
else
begin
For k:=0 to States [i,j]-1 do
begin
x:=WhereX;
Write (Wgt[k,i,j].Win,'/',Wgt[k,i,j].Wout,' ');
xx:=WhereX;
GotoXY (x,WhereY+1);
end; { for k... }
end; { else }
GotoXY (xx,y);
end; { for j...}
GotoXY (1,WhereY+Radix);
end; { for i... }
end; {. with }
End; { Graf.Draw }
{ ------- Методы конечного автомата --------
*** Init ****
Установка режимов работы, вычисление вероятностей
мутаций и получение входной последовательности }
Constructor Avt.Init;
var
i: 1..MaxMut;
s: real;
x: ValLenType;
c: char;
ec:integer;
Begin
Inherited Init;
s:=0;
FillChar (ValsOut, SizeOf(ValsOut),Radix);
For x:=0 to ValLen do Value [x]:=GetVal(x);
Steps :=0;
NMuts:=0;
Config;
For i:=1 to MaxMut do
begin
s:=s+Ver[i];
Vers[i]:=s;
end;
Best:=Body;
If not Trace then Writeln ('Пожалуйста подождите...');
End; { Avt.Init }
{ **** Oonfig **** Задание опций для генерации автомата }
Procedure Avt.Config;
Procedure TraceMode;
Begin
Trace:=true;
End;
Procedure RandMut;
Begin
Randomize;
End;
Procedure ManualVers;
const
verstr:array[MutType] of string =
('добавления состояния','удаления состояния', 'переброски связи',
'изменения веса', 'изменения начального состояния');
var
i: MutType;
c: char;
s: real;
Begin
Repeat
Repeat
ClrScr;
Writeln ('Вероятности...');
For i:=1 to MaxMut do
Writeln (i,'......',verstr[i]);
Writeln ('Enter..Принять эти вероятности');
For i:=1 to MaxMut do
begin
GotoXY (40,i+1);
Write (Ver[i]:10:8);
end;
c:=GetKey (Keys12345Ent, false);
If c=Enter then break;
i:=byte (c)-byte('O');
GotoXY (1 ,10);
Write ('Введите вероятность ',verstr[i],'> ');
Ver[i]:=GetReal (0,1);
until false;
s:=0;
For i:=1 to MaxMut do s:=s+Ver[i];
If (s<1-VerErr) or (s>1+VerErr) then
begin
GotoXY(10, 10);
Writeln ('Сумма вероятностей должна быть равна 1, а не ',s:10:8);
ReadKey;
end;
until (s>1-VerErr) and (s<1+VerErr);
End;
Procedure ManualVals;
var
x:ValLenType;
Begin
ClrScr;
Repeat
Clrscr;
Writeln('Введите ',ValLen+1,' знач. входной последоват.');
For x:=0 to ValLen do
begin
Write (x,'>');
Value [x]:=GetNum (0,MaxNum);
end;
until Confirm;
End;
Procedure Confirmation;
Begin
ClrScr;
Write ('Введите количество мутаций, после которого запрашивать ' +
'подтверждение ');
Steps:=GetNum(0,$7FFFFFFF);
End;
type
ba=array[1..6] of boolean;
const
opt: ba= (false, true, false, false, false, false);
var
c:char;
i:byte;
Begin
Writeln (
'1......Пошаговый режим НЕТ'#13#10,
'2......Случайные мутации ДА'#13#10,
'3......Задание вероятностей мутаций НЕТ'#13#10,
'4......Задание входной последовательности НЕТ'#13#10,
'5......Периодический запрос подтверждения НЕТ'#13#10,
'6......Задание исходного автомата НЕТ'#13#10,
'Enter..Начало генерации конечного автомата'#13#10,
'Esc....Выход');
GotoXY (1,25);
Write ('');
Repeat
c:=GetKey (Keys1_6EE,false);
Case c of
Enter:break;
Esc:Halt (1 );
end;
i:=byte(c)-byte('0');
opt[i]:=not opt[i];
GotoXY (56,i);
If opt[i] then Write ('ДА ') else Write ('НЕТ');
until false;
If opt[1] then TraceMode;
If opt[2] then RandMut;
If opt[3] then ManualVers;
If opt[4] then ManualVals;
If opt[5] then Confirmation;
If opt[6] then Advlnit;
ClrScr;
End; { Avt.Config }
{ **** Advlnit ****
Ввод автомата вручную. Перекройте этот метод, если в качестве исходного необходимо взять какой-то определенный автомат. }
Procedure Avt.Advlnit;
{ Если необходим исходный автомат с 3-мя состояниями и связями:
1 1 2 3
1 1/0 0/0 ---
2 --- 0/1 1/0 ---
3 --- 0/1 1/1 ---
этот метод должен выглядеть примерно так:
var
W:WgtRec;
i:Index;
}
var c:char;
Begin
{ For i:=1 to 3 do AddState;
W.in :=1; W.out :=0; AddAdj (1, 1 ,W);
W.in :=0; W.out :=0; AddAdj (1, 2, W);
W.in :=0; W.out :=1; AddAdj (2, 2, W);
W.in :=1; W.out :=0; AddAdj (2, 2, W);
W.in :=0; W.out :=1; AddAdj (3, 2, W);
W.in :=1; W.out :=1; AddAdj (3 3,W) }
Repeat
ClrScr;
Window(1,1,80,25);
Graf.Draw;
Writeln ('Начальное состояние: ',Body.First);
Window (45,1,80,25);
Writeln (
'1...Добавить состояние и выходы из него'#13#10 +
'2...Удалить последнее состояние'#13#10+
'3...Перебросить связь на другое состояние'#13#10+
'4...Изменить выходной вес связи'#13#10+
'5...Принять другое состояние в качестве входа',
#13#10'Esc.Принять этот автомат за исходный');
c:=GetKey(Keys12345Esc,false);
Case c of
'1': AddState;
'2': DelState;
'3': DelAdj_ask;
'4': ChangeWgt_ask;
'5': ChangeFirst_ask;
end;
until c=Esc;
Window (1, 1, 80, 25);
ClrScr;
End; {. Avt.AdvInit }
{ **** DoTheBest ****
Сгенерировать автомат, отвечающий заданным требованиям. Генерация осуществляется так:
1) Осуществляется какая-нибудь мутация и вычисляется коэффициент
2) Если он больше, чем у текущего Best, то этот автомат сохраняется, в гпээтивном случае восстанавливается прежний автомат. }
Procedure Avt.DoTheBest;
var
c:char;
Begin
Repeat
Repeat
Mutation
until not GrafError;
GetKoef;
If Trace then
begin
Window (55,1,80,4);
Writeln ('F8...Шаг'#13#10+
'F9...Выполнение до конца'#13#10+
'Esc..Выход');
Window (1,1,80,25);
Repeat
Repeat
c:=ReadKey;
If c=Esc then Exit;
until c=#0;
c:=ReadKey
until c in [F8, F9];
If c=F8 then
begin
ClrScr;
Draw;
end
else
begin
Write ('OK'#7);
ClrScr;
Write ('Please wait...');
Trace:=false;
end;
end;
If IsBest then
begin
Store;
Inc (NMuts);
If (Steps<>0) and (NMuts mod Steps=0) and not Trace then
begin
Write(#13'Произошло ',Nmuts,' мутаций. Продолжить? (Y/N)');
c:=UpCase(GetKey (KeysYN, true));
DelLine;
If c='N' then Break;
end;
end
else Restore;
until Best.Koef>=IdealKoef-1e-10;
End;
{ *** Draw ***
Вывод автомота на экран вместе с результатами его деятельности }
Procedure AVT. Draw;
Procedure WriteMas (var m:ValType;start:byte);
var i:0..ValLen;
Begin
For i:=start to ValLen do
Write (m[i],' ');
End; { Avt.Draw.WriteMas }
Begin
Inherited Draw;
Window (45,10,80,25);
Write ('ВХОД: ');
WriteMas (Value,0);
Write (#13#10'ВЫХОД: ');
WriteMas (ValsOut,1);
Writeln (#13#10'Интеллект:',Body.Koef:5:2);
Writeln ('Начальное состояние: ',Body.First);
Writeln ('Количество мутаций: ',NMuts);
Window (1,1,80,25);
End; { Avt.Draw } { **** Mutation ****
Случайная мутация конечного автомата.
Если в процессе мутации пг^кчошла ошибка, то флаг GrafError поднят }
Procedure Avt.Mutation;
Begin
GrafError:=false;
Case MutNum of
1:AddState;
2:DelState;
3:_DelAdj;
4:_ChangeWgt;
5:_ChangeFirst;
end;
End; { Avt.Mutation }
{ *** store ****
Сохранить текущий автомат для дальнейшей селекции }
Procedure Avt.Stor

 сигналов из конечного алфавита. На рис. 1 представлен конечный автомат М с тремя состояниями A, B, C алфавит входных символов автомата состоит из символов а, b, с, а выходных – из
сигналов из конечного алфавита. На рис. 1 представлен конечный автомат М с тремя состояниями A, B, C алфавит входных символов автомата состоит из символов а, b, с, а выходных – из  двухуровневую процедуру, блок-схема которой приведена на рис. 2, где 1 – алгоритм структурной адаптации; 2 – алгоритм использования; 3 – алгоритм параметрической адаптации.
двухуровневую процедуру, блок-схема которой приведена на рис. 2, где 1 – алгоритм структурной адаптации; 2 – алгоритм использования; 3 – алгоритм параметрической адаптации.
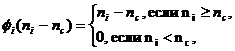
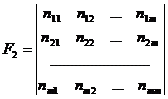 , (2)
, (2)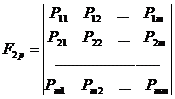 , (3)
, (3)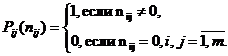 (4)
(4) ,
, 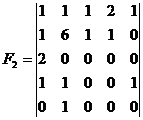 .
.