Распознавание объектов с качественными характеристиками
В большинстве случаев образы и отдельные изображения характеризуются с помощью количественных характеристик: геометрических размеров, веса, площади, объема и т. д. В этих случаях количественные изменения характеристик конкретного изображения обычно не сразу ведут к изменению образа, к которому относится распознаваемое изображение. Только достигнув определенных для каждого образа границ, количественные изменения вызывают качественный скачок - переход к другому образу. Образы и конкретные изображения могут характеризоваться не только количественными, но и качественными характеристиками (свойствами, признаками, атрибутами). Эти признаки не могут быть описаны (или обычно не описываются) количественно, например, цвет, вкус, ощущение, запах. Образы либо обладают какими-то качественными характеристиками, либо не обладают.
Между качественными и количественными характеристиками образов есть существенное различие, однако это различие во многих случаях нельзя абсолютизировать, поскольку каждому качественному атрибуту присущи и определенные интервалы изменения количественных характеристик, за пределами которых меняется и качественный атрибут. Например, определенному цвету изображения соответствует конкретный диапазон длин электромагнитных волн, за пределами которого цвет изменится.
Существуют различные подходы к распознаванию изображений с качественными характеристиками. В данной лабораторной работе рассмотрим один из них, основанный на двоичном кодировании наличия или отсутствия какого-либо качественного признака. В рассматриваемом подходе конкретное изображение Xk некоторого образа с качественными характеристиками представляется в виде двоичного вектора
Xk = (xk1, xk2, …, xkj, …, xkn),
где n - размерность пространства признаков.
Если изображение Xk обладает j-м признаком, то xkj =1, а если нет, то xkj = 0, т. е. здесь отождествляется объект и двоичный вектор, его описывающий.
Рассмотрим в качестве примера четыре объекта (вишня, апельсин, яблоко, дыня), каждый из которых имеет три признака: цвет, наличие косточки или семечек (табл. 1). В табл. 2 приведены числовые значения признаков для рассматриваемого примера после их двоичного кодирования.
Наиболее простой метод решения задач распознавания объектов с качественными характеристиками после двоичного кодирования атрибутов - свести решение исходной задачи к решению задачи распознавания объектов с количественными характеристиками в n-мерном векторном пространстве. Для этого необходимо для каждого качественного признака ввести в n-мерном векторном пространстве ось. Если для рассматриваемого объекта признак существует, то на оси откладывается единица, если нет - то нуль. В результате получается многомерное двоичное пространство признаков, где можно использовать различные расстояния, применяемые для распознавания объектов с количественными характеристиками.
Таблица 1
|
Вектор признаков |
Желтый цвет |
Оранжевый цвет |
Красный цвет |
Есть косточка |
Есть семечки |
Вишня |
X1 |
нет |
нет |
да |
да |
нет |
Апельсин |
X2 |
нет |
да |
нет |
нет |
да |
Яблоко |
X3 |
да |
нет |
да |
нет |
да |
Дыня |
X4 |
да |
нет |
нет |
нет |
да |
Таблица 2
|
Вектор признаков |
Желтый цвет |
Оранжевый цвет |
Красный цвет |
Есть косточка |
Есть семечки |
Вишня |
X1 |
x11 = 0 |
x12 = 0 |
x13 = 1 |
x14 = 1 |
x15 = 0 |
Апельсин |
X2 |
x21 = 0 |
x22 = 1 |
x23 = 0 |
x24 = 0 |
x25 = 1 |
Яблоко |
X3 |
x31 = 1 |
x32 = 0 |
x33 = 1 |
x34 = 0 |
x35 = 1 |
Дыня |
X4 |
x41 = 1 |
x42 = 0 |
x43 = 0 |
x44 = 0 |
x45 = 1 |
В рассматриваемом примере в результате введения количественных характеристик вместо качественных признаков (табл. 2) получается пятимерное двоичное пространство, где можно применять расстояния по Евклиду (1), по Минковскому (2), расстояние, использующее сумму модулей разностей между соответствующими компонентами n-мерных векторов (3):
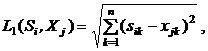 (1)
(1)
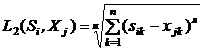 , (2)
, (2)
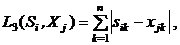 (3)
(3)
где 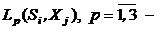 соответствующее расстояние между входным изображением
соответствующее расстояние между входным изображением 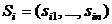 и эталонным изображением
и эталонным изображением 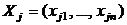
 j-го образа;
j-го образа; 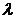 - целое положительное число, большее двух.
- целое положительное число, большее двух.
Расстояния (1) - (3) могут использоваться также и с весовыми коэффициентами.
При двоичном кодировании качественных признаков может применяться и расстояние по Хеммингу, которое вводится для любых двоичных векторов. Расстояние по Хеммингу между двумя двоичными векторами равно числу несовпадающих двоичных компонент векторов. Если вектора имеют все одинаковые компоненты, то расстояние между ними равно нулю, если вектора не имеют совпадающих компонент, то расстояние равно размерности векторов.
Более тонкая классификация объектов с качественными признаками получается при введении для каждой пары объектов Xj, Xi, для которых введено двоичное кодирование качественных признаков, переменных, характеризующих их общность или различие с помощью табл. 3.
Таблица 3
Переменная a в табл. 3 предназначена для подсчета числа общих признаков объектов Xj, и Xi . Она может быть вычислена с помощью соотношения
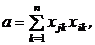
где xjk, xik - двоичные компоненты векторов, описывающих объекты Xj, и Xi.
С помощью переменной b подсчитывается число случаев, когда объекты Xj и Xi не обладают одним и тем же признаком, 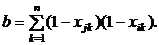 Переменные g и h предназначены соответственно для подсчета числа признаков, присутствующих у объекта Xi и отсутствующих у объекта Xj, и, присутствующих у объекта Xj и отсутствующими у объекта Xi,
Переменные g и h предназначены соответственно для подсчета числа признаков, присутствующих у объекта Xi и отсутствующих у объекта Xj, и, присутствующих у объекта Xj и отсутствующими у объекта Xi, 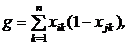
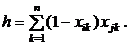
Из анализа переменных a, b, g, h следует, что, чем больше сходство между объектами Xj и Xi, тем больше должна быть переменная a, т.е. мера близости объектов или функция сходства должна быть возрастающей функцией от a, функция сходства должна быть симметричной относительно переменных g и h. Относительно переменной b однозначный вывод сделать не удается, поскольку, с одной стороны, отсутствие одинаковых признаков у объектов может свидетельствовать об их сходстве, однако, с другой стороны, если у объектов общим является только отсутствие одинаковых признаков, то они не могут относиться к одному классу.
Наиболее часто применяются следующие функции сходства:
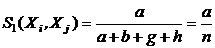 (функция сходства Рассела и Рао),
(функция сходства Рассела и Рао),
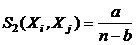 (функция сходства Жокара и Нидмена),
(функция сходства Жокара и Нидмена),
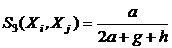 (функция сходства Дайса),
(функция сходства Дайса),
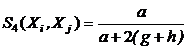 (функция сходства Сокаля и Снифа),
(функция сходства Сокаля и Снифа),
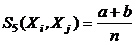 (функция сходства Сокаля и Мишнера),
(функция сходства Сокаля и Мишнера),
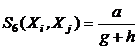 (функция сходства Кульжинского),
(функция сходства Кульжинского),
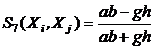 (функция сходства Юла).
(функция сходства Юла).

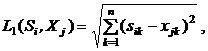 (1)
(1)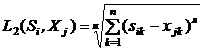 , (2)
, (2)