Существует большое число различных форм представления изображений в распознающих устройствах или программах. Одной из наиболее простых и понятных является форма, использующая представление изображений в виде точек или векторов в некотором n-мерном пространстве. Каждая ось такого пространства естественным образом соотносится с одним из n входов или с одним из n рецепторов распознающей системы. Каждый из рецепторов может находиться в одном из m состояний, если они дискретны, или иметь бесконечно большое число состояний, если рецепторы непрерывны. В зависимости от вида используемых рецепторов может порождаться непрерывное, дискретное или непрерывно-дискретное n-мерноепространство. В данной лабораторной работе рассматривается непрерывное n-мерноевекторное пространство.
Мера сходства изображений в n-мерном векторном пространстве вводится как функцию двух переменных L(Sk, Si), где Sk, Si є S; S = {S1, S2, …, Sn} - конечное множество изображений в рассматриваемом пространстве. При этом функция L(Sk, Si) обладает следующими свойствами:
- свойством симметрии, т.е. L(Sk, Si) = L(Si, Sk);
- областью значений функции является множество неотрицательных чисел, т.е. L(Sk, Si) > или = 0, k, i = 1, 2, …, n;
- мера сходства изображения с самим собой принимает экстремальное значение по сравнению с любым другим изображением, т.е. в зависимости от способа введения меры сходства выполняется одно из двух соотношений:
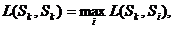
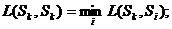
- в случае компактных образов функция L(Sk, Si) является монотонной функцией удаления точек Sk и Si друг от друга в n-мерном пространстве.
В n-мерном пространстве мера сходства изображений может быть введена многими способами. Рассмотрим несколько из них. При этом во всех случаях будем полагать, что эталонные изображения X1, X2, …, Xm m различных классов изображений или образов в n-мерном пространстве задаются в виде векторов с проекциями на оси координат: X1 = (x11, x12, …, x1n), X2 = (x21, x22, …, x2n), …, Xm = (xm1, xm2, …, xmn). Любое входное изображение Si є S также представляется в виде вектора Si = (si1, si2, …, sin) в этом пространстве.
1. Распознавание по углу между векторами
Мера близости между двумя векторами в n-мерном векторном пространстве может быть задана в виде угла. Если задано входное изображение Si = (si1, si2, …, sin) и векторы эталонных изображений X1 = (x11, x12, …, x1n), X2 = (x21, x22, …, x2n), …, Xm = (xm1, xm2, …, xmn), то мера сходства между входным и эталонными изображениями определяется выражением
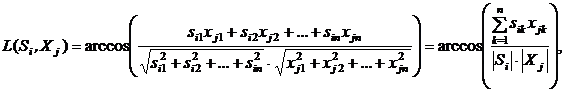 (1)
(1)
где 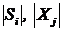 - соответственно длины векторов
- соответственно длины векторов 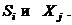
Принадлежность входного изображения Si к одному из m образов определяется с помощью решающего правила
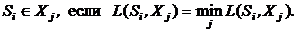 (2)
(2)
При этом в решающем правиле и далее по тексту для обозначения j-го образа и эталонного изображения j-го образа применяется одно и тоже обозначение 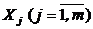 .
.
2. Распознавание изображений по скалярному произведению
Мера близости изображений по углу между векторами (1) основана на скалярном произведении векторов:
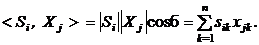 (3)
(3)
Некоторые системы распознавания используют непосредственно скалярное произведение в качестве меры сходства изображений в n-мерном векторном пространстве:
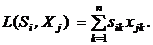 (4)
(4)
В этом случае принадлежность входного изображения Si к какому-либо образу определяется с помощью решающего правила
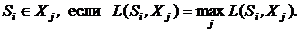 (5)
(5)
3. Распознавание изображений по принадлежности к заданной области пространства
При этом способе распознавания все пространство изображений V разбивается на непересекающиеся области V1, V2, …, Vm, Vm+1, где V1, V2, …, Vm - области, содержащие изображения только одного соответствующего образа X1, X2, …, Xm; Vm+1 - область, не содержащая изображений, относящихся к указанным образам. В этом случае принадлежность входного изображения Si = (si1, si2, …, sin) к некоторому j-му образу 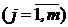 определяется решающим правилом
определяется решающим правилом
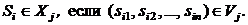 (6)
(6)
Если области 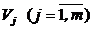 заданы в евклидовом пространстве в виде шаров с центрами в точках
заданы в евклидовом пространстве в виде шаров с центрами в точках 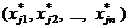 и радиусами Rj, то решающее правило (6) принимает вид
и радиусами Rj, то решающее правило (6) принимает вид
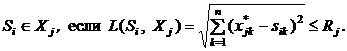 (7)
(7)
Для конструирования областей в пространстве изображений могут использоваться любые меры сходства, например, расстояния с весовыми коэффициентами (8) - (10), расстояние по Камберра (11) и т.д.
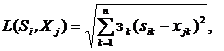 (8)
(8)
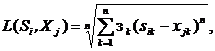 (9)
(9)
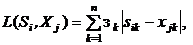 (10)
(10)
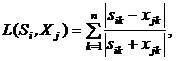 (11)
(11)
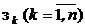 - весовые коэффициенты; l - целое положительное число, большее двух.
- весовые коэффициенты; l - целое положительное число, большее двух.
Решающее правило (6) для расстояний (8) - (10) принимает вид
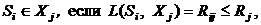
где Rij - расстояние, заданное одним из выражений (8) - (11), между предъявленным изображением Si и центром шара, содержащего изображения j-го образа; Rj - радиус шара, содержащего изображения j-го образа.
При использовании для распознавания угла между векторами непересекающиеся области 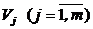 задаются в виде конусов, а решающее правило имеет вид
задаются в виде конусов, а решающее правило имеет вид
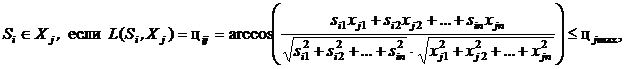
где 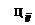 - угол между предъявленным изображением Si и эталонным изображением Xj;
- угол между предъявленным изображением Si и эталонным изображением Xj;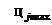 - предельно допустимый угол для j-го образа между эталонным и распознаваемым изображениями.
- предельно допустимый угол для j-го образа между эталонным и распознаваемым изображениями.

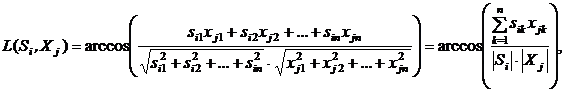 (1)
(1)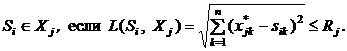 (7)
(7) 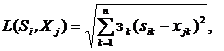 (8)
(8)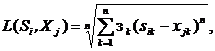 (9)
(9)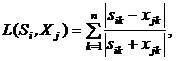 (11)
(11)