Другим подходом к решению проблемы взаимоблокировок является устранение взаимоблокировок.3. В случае предотвращения взаимоблокировок мы накладывали определенные ограничения на запросы к ресурсам, с тем, чтобы сделать невозможным осуществление, по крайней мере, одного из необходимых условий существования взаимоблокировок и тем самым предотвратить саму возможность их возникновения. К сожалению, этот метод приводит к неэффективному использованию ресурсов и снижению скорости работы процесса. Устранение взаимоблокировок допускает наличие трех необходимых условий возникновения взаимоблокировок, но мы принимаем меры к тому, чтобы ситуация взаимного блокирования процессов не могла быть достигнута. Соответственно, устранение взаимоблокировок обеспечивает большую параллельность вычислений, чем предотвращение. Решение о том, способен ли текущий запрос ресурса в случае его удовлетворения привести к возникновению ' взаимоблокировки, принимается в этом случае динамически (и, следовательно, при использовании данной технологии необходимо знать о том, какие ресурсы потребуются процессу в дальнейшем).
В этом разделе мы познакомимся с двумя подходами к устранению взаимоблокировок.
Не запускать процесс, если его запросы могут привести к взаимоблокировке.
Не удовлетворять запросы процесса, если их выполнение способно привести
к взаимоблокировке.
Запрещение запуска процесса
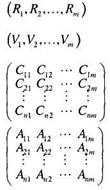
Ресурс = Доступность =
Требования = Распределение = |
Рассмотрим систему из п процессов и т различных типов ресурсов. Определим следующие векторы и матрицы:
Общее количество каждого ресурса в систе- ме
Общее количество каждого ресурса, не выделенного процессам
Запросы каждого процесса на каждый из ресурсов
Текущее распределение ресурсов
Матрица требований, в которой каждая строка описывает один из процессов, указывает максимальные требования каждого процесса к разным ресурсам, т.е. Сij — это требования процессом i ресурса j. Для работоспособности метода устранения взаимоблокировок эта информация должна быть объявлена процессом заранее. Аналогично, Aij — текущее количество ресурса j, выделенное процессу L
Должны выполняться следующие соотношения.
для всех i: все ресурсы либо свободны, либо выделены. |
для всех k и i: ни один процесс не может потребовать ресурс, пре- |
вышающий его общее количество в системе.
для всех k и i: ни один процесс не может получить больше ресур-
сов, чем было затребовано им.
Когда все указанные величины определены, мы в состоянии создать стратегию устранения взаимоблокировок, которая запрещает запуск нового процесса, если его требования ресурсов могут привести к взаимоблокировке. Новый процесс Pn+i запускается только если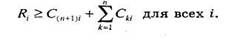
Это означает, что запуск нового процесса произойдет только в том случае, если могут быть удовлетворены максимальные требования всех текущих процессов плюс требования запускаемого процесса. Эта стратегия ни в коей мере не является оптимальной, поскольку предполагает худшее: что все процессы предъявят максимальные требования одновременно.
Запрет выделения ресурса
Стратегия запрета выделения ресурса, известная также как алгоритм банкира,4 впервые была предложена в работе [DIJK65]. Мы начнем рассмотрение с концепций состояния (state) и безопасного состояния (safe state). Остановимся на системе с фиксированным количеством процессов и фиксированным количеством ресурсов. В каждый момент времени процесс может иметь несколько выделенных ему ресурсов (или не иметь ни одного). Состояние системы представляет собой просто текущее распределение ресурсов по процессам. Следовательно, состояние можно представить как два ранее определенных вектора — ресурсов и доступности — и две матрицы — требований и распределения. Безопасное состояние — это такое состояние, в котором имеется, по крайней мере, одна последовательность, которая не приводит к взаимоблокировке (т.е. все процессы могут быть выполнены до завершения). Состояние, не являющееся безопасным, называется, соответственно, опасным состоянием.
Описанную концепцию иллюстрирует приведенный далее пример. На рис. 6.6,о показано состояние системы, образованной четырьмя процессами и тремя ресурсами. Общее количество ресурсов Rl, R2 и R3 составляет соответственно 9, 3 и 6 единиц. В результате сделанного к этому моменту распределения ресурсов по процессам доступными остались по одной единице ресурсов R2 и R3. Безопасно ли данное состояние? Для ответа на этот вопрос зададимся другим вопросом, а именно — может ли какой-нибудь из четырех процессов быть выполнен при данных доступных ресурсах до завершения? Или, говоря иначе, могут ли при данном распределении ресурсов быть удовлетворены максимальные требования какого-то из процессов за счет оставшихся ресурсов? Ясно, что для процесса Р1 это невозможно, так как у него имеется только одна единица ресурса R1, и для полного удовлетворения ему требуется еще по две единицы ресурсов Rl, R2 и R3. Однако если выделить процессу Р2 одну единицу ресурса R3, то будут удовлетворены максимальные требования этого процесса и он сможет быть завершен.
4 Дейкстра воспользовался таким названием, сравнивая эту задачу с деятельностью банка, где клиент, который хочет осуществить заем денег, отождествляется с процессом, а деньги — с ресурсом. Банк имеет ограниченное количество денег для займов, и список клиентов, у каждого из которых имеется своя предельная величина кредита. Клиент может неоднократно осуществлять заем в пределах этой величины, причем нет никакой гарантии, что он погасит хотя бы часть задолженности до того момента, пока не займет всю возможную сумму. Таким образом, если несколько клиентов берут частичные займы, то гарантировать возврат этих денег банку может только некоторый резервный фонд. В худшем случае, когда все клиенты погашают займы только по достижении ими предельной суммы кредита, этот фонд должен обеспечить возможность выдать им эти максимальные суммы. Следовательно, при исчерпании денежных запасов до размеров резервного фонда банк будет вынужден отказать очередному клиенту в предоставлении займа, иначе деньги в банк могут никогда не вернуться.
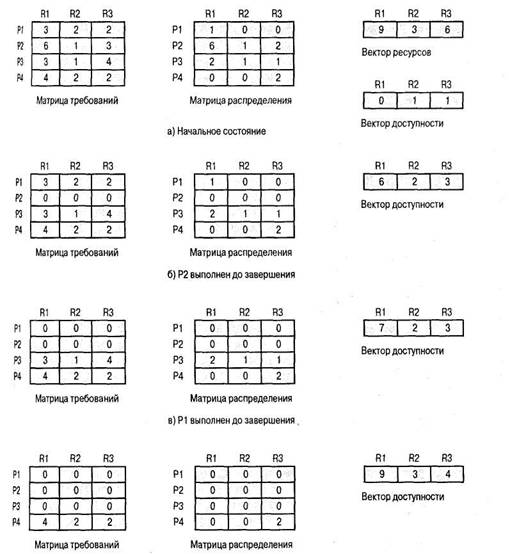
г) РЗ выполнен до завершения
Рис. 6.6. Определение безопасного состояния
Предположим, что именно так и произошло — процесс Р2 оказался завершен, и распределенные ему ресурсы вернулись в пул доступных. Это состояние системы показано на рис. 6.6,6. Вернувшись к вопросу о том, какой из процессов может быть завершен в данной ситуации, мы находим, что могут быть удовлетворены максимальные требования как процесса Р1, так и процесса РЗ. Предположим, что мы выбрали процесс Р1. По его завершении и возвращении захваченных им ресурсов в пул доступных ситуация будет выглядеть так, как показано на рис. 6.6,в. И наконец, по завершении процесса РЗ мы придем к состоянию, изображенному на рис. 6.6,г. К этому моменту все процессы завершены, а, следовательно, исходное состояние (рис. 6.6,а) является безопасным.
Описанная концепция автоматически приводит к стратегии устранения взаимоблокировок, которая гарантирует, что система процессов и ресурсов всегда находится в безопасном состоянии. Когда процесс делает запрос к некоторому множеству ресурсов, предполагается, что запрос удовлетворен, после чего определяется, является ли обновленное состояние системы безопасным. Если это так, то запрос удовлетворяется; в противном случае процесс блокируется до тех пор, пока удовлетворение его запроса не станет безопасным.
Рассмотрим состояние, определяемое матрицей на рис. 6.7,а. Предположим, что процесс Р2 делает запрос на одну дополнительную единицу ресурса R1 и одну — ресурса R3. Если запрос будет выполнен, то в результате состояние системы станет таким, как показано на рис. 6.6,а. Мы уже видели, что это состояние является безопасным. Таким образом, запрос можно удовлетворить. Теперь вернемся к состоянию, представленному на рис. 6.7,а, и предположим, что такой же запрос на одну дополнительную единицу ресурса R1 и одну — ресурса R3 делает процесс Р1. Если этот запрос будет удовлетворен, состояние системы станет таким, как показано на рис. 6.7,6. Является ли это состояние безопасным? В данном случае ответ — нет, поскольку каждому из процессов требуется по одной дополнительной единице ресурса R1, а в наличии свободных единиц этого ресурса уже нет. Следовательно, запрос процесса Р1 должен быть отклонен, а сам процесс блокирован.
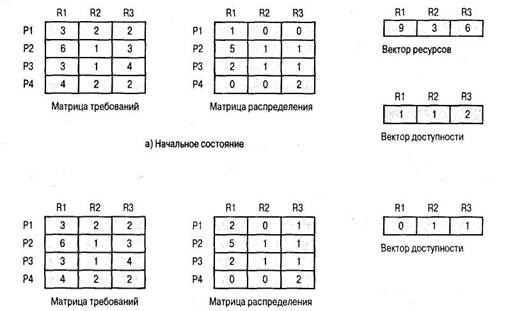
б) Процесс Р1 запрашивает по одной единице ресурсов R1 и R3
Рис. 6.7. Определение опасного состояния
Важно отметить, что состояние, представленное на рис. 6.7,6, не является взаимоблокировкой. Оно всего лишь может привести к ней. Например, при работе процесс Р1 может освободить по одной единице ресурсов R1 и R3, и система вновь вернется в безопасное состояние. Следовательно, стратегия устранения взаимоблокировок не занимается точным предсказанием взаимоблокировок; она лишь предвидит их возможность и устраняет ее.
В листинге 6.1 приведена логика работы алгоритма устранения взаимоблокировок. Основной алгоритм показан в части б. Состояние системы описывается структурой state, а вектор request [*] определяет ресурсы, затребованные процессом i. Сначала выполняется проверка того, что запрос не превышает исходные требования процесса. Если запрос корректен, то следующий шаг алгоритма состоит в определении возможности удовлетворения запроса (т.е. выяснении, достаточно ли для этого свободных ресурсов). Если нет — процесс приостанавливается; если же ресурсов достаточно, выполняется последняя проверка — безопасно ли выполнение запроса. Для этого процессу гипотетически выделяются требуемые ресурсы, в результате чего получается новое состояние системы newstate, которое и проверяется на безопасность с использованием алгоритма из листинга 6.1,в.
Листинг 6.1. Алгоритм устранения взаимоблокировок
 struct state
struct state
int resource [m] ;
int available [m] ; int claim[n] [m] ; int alloc[n] [m]; 1
а) Глобальная структура данных
if (alloc[i,*]+ request[*] > claim[i,*])
(
<Ошибка > /* Суммарный запрос превышает требования */
1
else if (request [*]>available[*])' (
< Приостановка процесса >
}
else /* Моделируем выполнение запроса */
I
<Определение нового состояния:
alloc[i,*] = alloc[i,*]+ request[*];
available[*] = available [*]- request[*];
>
1
if(safe(newstate))
(
<Выполнение распределения >
}
else {
Восстановление исходного состояния >
Приостановка процесса >
}
б)Алгоритм выделения ресурсов
boolean safe(state S)
1
int currentavail [m] ;
process rest[<Количество процессов>]; ,currentavail = available; rest = { Все процессы }; possible = true; while(possible) {
< Найти Pk в rest такой, что
claimfk,*] - allocfk,*] <= currentavail; >
if (<Найден>) /* Моделирование выполнения Рк */
{
currentavail = currentavail + allocfk,*]; rest = rest - {Pk}; } else
possible = false; }
return (rest == NULL); }
в) Проверка безопасности алгоритма (алгоритм банкира)
Устранение взаимоблокировок обладает тем достоинством, что при его использовании не нужны ни перераспределение, ни откат процессов, как в случае обнаружения взаимоблокировок; кроме того, этот метод накладывает меньше ограничений по сравнению с предотвращением взаимоблокировок. Однако использование этого метода требует выполнения определенных условий.
Должны быть заранее указаны максимальные требования каждого процесса
к ресурсам.
Рассматриваемые процессы должны быть независимы, т.е. порядок их выпол-
нения не должен ограничиваться никакими требованиями синхронизации.
Должно иметься фиксированное количество распределяемых ресурсов.
Ни один процесс не должен завершаться в состоянии захвата ресурсов.
ОБНАРУЖЕНИЕ ВЗАИМОБЛОКИРОВОК
Стратегии предотвращения взаимоблокировок весьма консервативны; они решают проблему взаимоблокировок путем ограничения доступа процессов к ресурсам и наложения ограничений на процессы. Их противоположность — стратегии обнаружения взаимоблокировок, которые не ограничивают доступ к ресурсам и не налагают никаких ограничений на действия процессов. При обнаружении взаимоблокировок запрошенные ресурсы выделяются процессам при первой возможности. Периодически операционная система выполняет алгоритм, который позволяет обнаружить условия циклического ожидания (см. рис. 6.5).
Алгоритм обнаружения взаимоблокировки
Проверка наличия взаимоблокировки может выполняться как при каждом запросе ресурса, так и менее часто, в зависимости от того, насколько вероятно
возникновение взаимоблокировки. С одной стороны, проверка при каждом запросе ресурса имеет два основных преимущества: раннее обнаружение и упрощение алгоритма, поскольку он основан на инкрементальных изменениях состояния системы. С другой стороны, столь частая проверка приводит к заметному потреблению времени процессора.
Обобщенный алгоритм обнаружения взаимоблокировок описан в [COFF71]. В нем используются матрица распределения и вектор доступности, описанные в предыдущем разделе. Кроме того, определена матрица запросов Q такая, что qtj представляет собой количество ресурсов типа j, затребованное процессом i. Алгоритм работает, помечая незаблокированные процессы. Изначально все процессы не помечены. После этого выполняются следующие шаги.
Помечаем все процессы, у которых строки в матрице распределения состоят из одних нолей.
Временный вектор W инициализируем значениями вектора доступности.
Находим индекс i, такой, что процесс i в настоящий момент не помечен, и i-я строка матрицы Q не превышает W, т.е. для всех \<к<т выполняется Qjk < Wk. Если такой строки нет, алгоритм прекращает свою работу.
Если такая строка имеется, помечаем процесс i и добавляем соответствую строку матрицы распределения к W, т.е. выполняем присвоение Wk =Wk+ A4 для всех 1 < к < т. Возвращаемся к шагу 3.
Взаимоблокировка имеется тогда и только тогда, когда после выполнения алгоритма есть непомеченные процессы; каждый непомеченный процесс заблокирован. Стратегия этого алгоритма состоит в поиске процесса, запросы которого могут быть удовлетворены доступными ресурсами, а затем предполагается, что эти ресурсы ему выделены и процесс, завершив свою работу, освобождает их. После этого алгоритм приступает к поиску другого процесса, который может успешно завершить свою работу. Заметим, что данный алгоритм не гарантирует предотвращения взаимоблокировок — это зависит от порядка удовлетворения запросов процессов. Все, что делает данный алгоритм, — это определяет, имеется ли взаимоблокировка в настоящий момент.
Для иллюстрации алгоритма обнаружения взаимоблокировок рассмотрим рис. 6.8. Алгоритм работает следующим образом.
- Помечаем Р4, поскольку этот процесс не имеет распределенных ему ресурсов.
- Устанавливаем W = (0 0 0 0 1).
- Запрос процесса РЗ не превышает W, так что помечаем РЗ и устанавливаем W = W + (0 0 0 1 0) = (0 0 0 1 1).
- Других непомеченных процессов, строки матрицы Q которых не превышают W, нет. Алгоритм прекращает свою работу.
Таким образом, алгоритм позволяет заключить, что процессы Р1 и Р2 взаимно заблокированы.
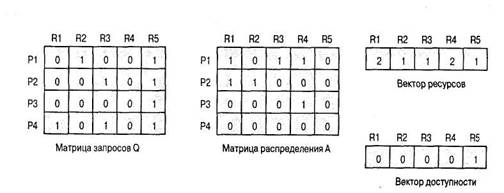
Рис. 6.8. Пример обнаружения взаимоблокировки
Восстановление
После того как взаимоблокировка обнаружена, требуется некоторая стратегия для восстановления нормальной работоспособности системы. Вот несколько возможных подходов к решению этой проблемы, перечисленные в порядке возрастания сложности.
- Прекратить выполнение всех заблокированных процессов. Хотите — верьте,
хотите — нет, но это самый распространенный подход, принятый в опера-
ционных системах.
- Вернуть каждый из заблокированных процессов в некоторую ранее опреде-
ленную точку и перезапустить все процессы. Для этого в систему должны
быть встроены механизмы отката и перезапуска. Самый большой риск при
таком подходе заключается в том, что взаимоблокировка может проявиться
вновь. Однако неопределенность относительных скоростей выполнения па-
раллельных вычислений обычно позволяет этого избежать.
- Последовательно прекращать выполнение заблокированных процессов по одно-
му до тех пор, пока взаимоблокировка не прекратится. Порядок выбора унич-
тожаемых процессов должен базироваться на некотором критерии минималь-
ной стоимости. После каждого уничтожения процесса должен быть вызван ал-
горитм обнаружения взаимоблокировок для проверки, не устранены ли они.
- Последовательно перераспределять ресурсы до тех пор, пока взаимоблоки-
ровка не прекратится. Как и в предыдущем случае, выбор процесса должен
осуществляться в соответствии с некоторым критерием минимальной стои-
мости, а после осуществления перераспределения должен вызываться алго-
ритм обнаружения взаимоблокировок. Процесс, ресурсы которого перерас-
пределяются, должен быть возвращен к состоянию, в котором он находился
до получения этого ресурса.
В случае использования вариантов 3 и 4 критерий выбора процесса может быть, например, одним из следующих:
процесс, потребляющий минимальное время процессора;
процесс с минимальным выводом информации;
процесс с наибольшим временем ожидания;
процесс с минимальным количеством захваченных ресурсов;
процесс с минимальным приоритетом.
При выборе критерия следует учитывать затраты времени на вычисление той или иной стоимости, а также отдавать себе отчет в том, что в данной ситуации понятие "стоимости" имеет смысл только для операционной системы в целом.