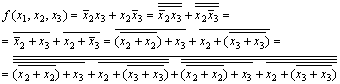Синтез и моделирование комбинационных устройств, заданных в табличной форме

Представление логической функции, заданной таблично, в аналитической форме

Любая таблично заданная логическая функция может быть представлена в совершенной нормальной дизъюнктивной форме (СНДФ) или в совершенной нормальной конъюнктивной форме (СНКФ). Совершенные формы, в отличие от нормальных форм, дают однозначное представление о функции.

СНДФ (так же как и нормальная дизъюнктивная форма) представляет собой совокупность минтермов объединенных знаком дизъюнкции.

СНКФ (как и нормальная конъюнктивная форма) представляет собой совокупность макстермов объединенных знаком конъюнкции.

Минтерм (конъюнктивный терм) – терм, связывающий переменные, представленные в прямой или инверсной форме, знаком конъюнкции.

Макстерм (дизъюнктивный терм) – терм, связывающий переменные, представленные в прямой или инверсной форме, знаком дизъюнкции.

Для представления таблично заданной логической функции в СНДФ необходимо выполнить следующие действия:

1. Выделить строки в таблице истинности, соответствующие единичному значению результата.
2. Записать минтермы для каждой строки (переменные со значением "1" учитываются в минтерме в прямом виде, а переменные со значением "0" – в инверсном).
3. Объединить полученные минтермы знаком дизъюнкции

Пример представления логической функции в СНДФ

Пусть дана логическая функция от трех переменных , заданная в табличной форме. Необходимо получить ее аналитическое представление в совершенной нормальной дизъюнктивной форме.

X1	X2	X3	y
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Аналитическое представление функции будет иметь вид:

=+++ (7.1)

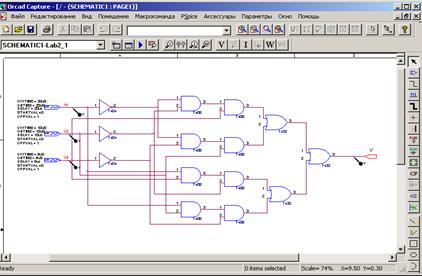
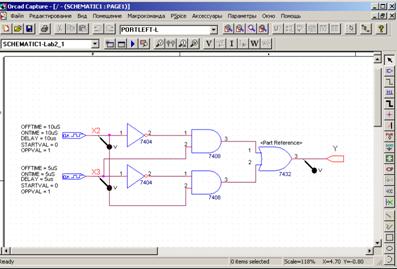
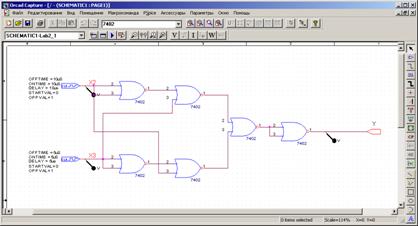
Согласно приведенному представлению, принципиальная электрическая схема должна состоять из логических элементов И, ИЛИ, НЕ и может иметь следующий вид:

Использование минимизация логических функций при автоматизации проектирования.

Минимизация логической функции – это процесс представления ее в виде минимального количества элементарных функций.
Наиболее универсальным методом минимизации функций является метод Квайна, позволяющий получить минимальное представление логических функций любого числа аргументов.

Общий принцип

Для минимизации функции по методу Квайна, необходимо, чтобы она была представлена в СНДФ. Метод заключается в пошаговом уменьшении ранга минтермов, входящих в состав ФАЛ и их количества.

Терминология

Импликанты – конъюнктивные термы переменного ранга.
Первичные импликанты – импликанты, входящие в выражения для минимизированной функции.
Существенные импликанты – импликанты, безусловно входящие в состав ФАЛ (т.е. каждая из них является единственной первичной импликантой, входящией в состав одного из первоначальных минтермов (минтермов СНДФ))
Нефункциональные импликанты – импликанты, не входящие в состав ни одного из минтермов.

Алгоритм минимизации

I этап.         Получение первичных импликант.
II этап.       Обработка первичныхимпликант
                а)            выделение существенных импликант.
                б)            исключение нефункциональных импликант

III этап. Составление минимальной комбинации импликант для покрытия оставшихся минтермов.

Пример 1

Пусть необходимо минимизировать следующее выражение:
+ +
I этап.
а) Получение импликант ранга 2 и 1.


1
	1
		1

В таблице нет пустых строк, след. ранг всех импликант уменьшен до 1.
Полученные импликанты:

Импликанты первого ранга всегда являются первичными, поэтому поиск первичных импликант закончен.

II этап.


V	V
V		V

Как видно, каждая из импликант является существенной, поэтому ФАЛ имеет вид
+

Пример 2

Пусть необходимо минимизировать следующее выражение:
+ +

I этап.
а) Получение импликант ранга 2 и 1.


1
	1
		1

В таблице одна пустая строка, которая соответствует импликанте , следовательно, она является первичной. При этом получена одна импликанта ранга 2 – . Т.к. она одна, то тоже является первичной.
II этап.


	V	V
V

Как видно, каждая из импликант является существенной, поэтому ФАЛ имеет вид
+

Пример минимизации логической функции при проектировании вычислительного устройства

Рассмотрим логическую функцию от трех переменных в соответствии с выражением (7.1).
I этап.
а) Получение импликант ранга 2 и 1.


1
	1
		1
			1

В таблице нет пустых строк, поэтому следующий ранг всех импликант уменьшен до 2.


	1
		1

В таблице все строки пустые, следовательно, минимальный ранг всех импликант составляет 2.
II этап.


V		V
	V		V

Как видно, каждая из импликант является существенной, поэтому ФАЛ имеет вид

Представление логических функций в различных базисах

Для представления логических функций в различных базисах можно воспользоваться правилами де Моргана:

Следствие из правил де Моргана:

Соответственно, для полученной ранее минимальной формы таблично заданной функции + в базисе (И, ИЛИ, НЕ) можно получить ее представление в базисе (И-НЕ) и базисе (ИЛИ-НЕ).

Представление логической функции в базисе И-НЕ:

+=
=
Согласно приведенному представлению, принципиальная электрическая схема должна состоять только из логических элементов И-НЕ и может иметь следующий вид:

Представление логической функции в базисе ИЛИ-НЕ:

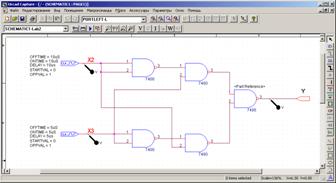
Согласно приведенному представлению, принципиальная электрическая схема должна состоять только из логических элементов ИЛИ-НЕ и может иметь следующий вид:

Последовательность действий при минимизации лочиских функций в различных базасах подробно была рассмотрена в разделе 4 данного пособия.