Экстремум ( англ. extremum, нем. Extremum n) - наибольшее и наименьшее значения функции на заданном множестве.
Различают:
- локальный - экстремум в некотором произвольно малом окрестности данной точки
- глобальный - экстремум во всей рассматриваемой области значений функций
Определение экстремума
Точка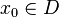 
называется точкой локального минимума ( максимума ) функции f : D -> R , если 
(для точки минимума), или 
(для точки максимума). Если знак неравенства строгий, то получим строгий локальный минимум ( максимум ).
Теорема Ферма
Пусть x 0 - точка экстремума функции f : D -> R . Если x 0 - внутренняя точка для D и f ( x ) - дифференцированная в точке 
, то f '( x 0 ) = 0 .
Теорема Ролля
Если f : [ a ; b ] -> R неперерервна на [a; b], дифференцированная на (a; b) и f ( a ) = f ( b ) , то
