Выпуклое множество

Выпуклое множество - подмножество евклидова пространства содержащей отрезок, соединяющий любые какие две точки этой множества.

Определение

Другими словами, множество $X \ in \ R ^ n$ называется выпуклой, если:

$\ Alpha x_1 + (1 - \ alpha) x_2 \ in X, \ quad \ forall x_1, x_2 \ in X, \, \ alpha \ in [0, 1].$

То есть, если множество X вместе с любыми двумя точками, которые принадлежат этому множеству, содержит отрезок, их соединяющий:

$[X_1, x_2] = \ left \ {x: \, x = x_2 + \ alpha (x_1 - x_2), \, \ alpha \ in [0, 1] \ right \}$ .

В пространстве 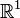$\ R ^ 1$ выпуклыми множествами будут прямая, полупрямой, отрезок, интервал, одноточечный множество.

В пространстве $\ R ^ n$ выпуклым будет само пространство, любое его линейный подпространство, шар, отрезок, одноточечный множество. Также, выпуклыми будут такие множества:

прямая $l_ {x_0 h}$ , проходящая через точку x 0 в направлении вектора h :

$l_ {\ mathbf x_0 h} = \ left \ {x \ in \ R ^ n: \, x = x_0 + \ alpha h, \ alpha \ in \ R ^ n \ right \}$ ;

луч $l_ {x_0 h} +$ , выходящий из точки x 0 в направлении вектора h :

$l_ {\ mathbf X 0h }^{+} = \ left \ {x \ in \ R ^ n: \, x = x_0 + \ alpha h, \, \ alpha \ ge 0 \ right \}$ ;

гиперплоскости H p? с нормалью p :

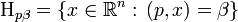$\ Mathrm H_ {p \ beta} = \ left \ {x \ in \ R ^ n: \, (p, x) = \ beta \ right \}$ ;

полупространства на которые гиперплоскости разделяет пространство:

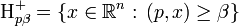$\ Mathrm H_ {p \ beta }^{+} = \ left \ {x \ in \ R ^ n: \, (p, x) \ ge \ beta \ right \}$ ,

$\ Mathrm H_ {p \ beta }^{-} = \ left \ {x \ in \ R ^ n: \, (p, x) \ le \ beta \ right \}$ .

Все перечисленные множества (кроме пули ) является частным случаем выпуклой множества полиэдры.

Свойства выпуклых множеств

Пересечение выпуклых множеств является выпуклым.
Линейная комбинация точек выпуклой множества выпуклая.
Выпуклая множество содержит любую выпуклую комбинацию своих точек.
Любую точку n -мерного евклидова пространства с выпуклой оболочки множества можно представить как выпуклую комбинацию не более n +1 точек этого множества.