Метод неопределенных множителей или метод неопределенных множителей Лагранжа - метод нахождения условного оптимума, предложенный итальянским математиком Жозефом-Луи Лагранжем. Метод позволяет свести задачу на отыскание условного оптимума в задаче на нахождение безусловного оптимума.
Задача
Пусть нужно найти оптимум функции n переменных  при s условиях
при s условиях
 , Где.
, Где.
Описание метода
Вводя s неопределенных множителей Лагранжа ? и, построим функцию Лагранжа
 .
.
Задача нахождения условного оптимума сводится к решению системы n + s уравнений с n + s переменными:
 ,
,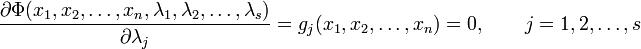 .
.
Использование
Метод неопределенных множителей Лагранжа широко используется в математической и теоретической физике. С помощью этого метода получены уравнения Лагранжа первого рода, которые позволяют формально ввести силы реакции в физические задачи с связями. Неопределенные множители Лагранжа использует также вариационный метод в квантовой механике.
Пример
Задача
Найти прямоугольник с наибольшей площадью при заданном периметре p.
Решение
Обозначим стороны прямоугольника x и y. Нужно найти максимум функции
- S = X Y
при условии
- 2 x + 2 y = p.
Вводим множитель Лагранжа ? и ищем безусловный оптимум функции
- F ( x, y, ?) = X Y - ? (2 x + 2 y - p )
Принимая производные получаем систему уравнений
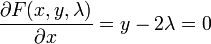


Подставляя значения y = 2? и x = 2? в последнее уравнение, получаем

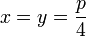 .
.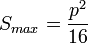
Итак, наибольшую площадь среди прямоугольников с заданным периметром имеет квадрат.