Квадратичное программирование ( англ. Q uadratic P rogramming, QP ) - особый тип оптимизационной задачи. Это задача оптимизации (сведение к минимуму или максимуму ) квадратичной функции нескольких переменных при линейных ограничениях на эти переменные.
Задачу квадратичного программирования можно сформулировать следующим образом:
Пусть x принадлежит пространству. Матрица N ? N Q симметрична, и c - любой N ? 1 вектор.
Минимизировать (относительно x )
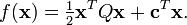
С учетом одного или нескольких ограничений в такой форме:
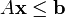( ограничение-неравенство )
( ограничение-равенство )
где 
указывает на транспонирование вектора. Обозначение 
означает, что каждый элемент вектора Ax меньше или равно соответствующего элемента вектора.
Если матрица 
является неотъемлимозначной, то f () является выпуклой функцией: в этом случае задача квадратичного программирования имеет глобальный минимум, если существует некоторый допустимый вектор x (вектор, удовлетворяющий ограничения) и если f () ограничена снизу в допустимой области. Если матрица Q является дополнительнозначной и задача имеет допустимое решение, то глобальный минимум является уникальным.
Если равно нулю, то задача становится задачей линейного программирования.
Связанная с этим задача квадратичного программирования с квадратичными ограничениями может быть поставлена добавлением квадратичных ограничений на переменные.
