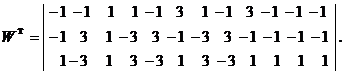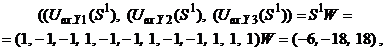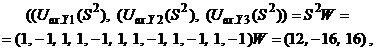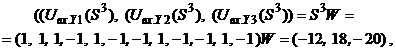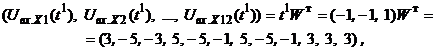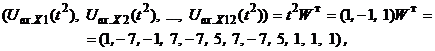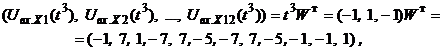|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
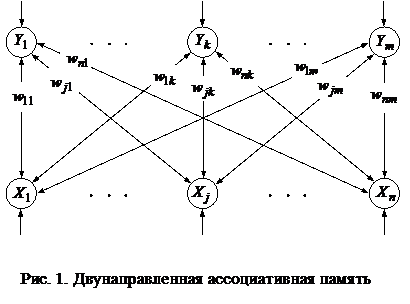
Двунаправленная ассоциативная память1. Двунаправленная ассоциативная память на двоичных элементахЛюбая нейронная сеть может рассматриваться как ассоциативная память, если хранимые в весах ее связей изображения являются аттракторами, поскольку любое входное изображение, попавшее в область притяжения аттрактора, может быть использовано для воспроизведения хранимой информации. Подобная память уже анализировалась в лабораторной работе, посвященной сетям Хопфилда. Сети Хопфилда позволяют по зашумленным или неполным изображениям восстанавливать хранимые, то есть исправлять и дополнять входные изображения, но не ассоциировать их с другими образами. Следовательно, сети Хопфилда обладают только автоассоциативной памятью. Это объясняется одноуровневой структурой сети, в которой входные и выходные изображения появляются на выходах одних и тех же элементов. Двунаправленная ассоциативная память (bidirectional associative memory, BAM) на двоичных элементах была предложена Коско в 1988 году. Архитектура сети представлена на рис. 1.
Сеть состоит из двух слоев нейронов, связанных парами двунаправленных взвешенных связей. Изображения (или n-мерныелибо m-мерные входные вектора) могут подаваться соответственно на входы X- или Y-элементов. При этом не предполагается подача изображений на оба слоя элементов одновременно. Если весовая матрица для сигналов, посылаемых из X-слоя элементов в Y-слой, есть
то весовая матрица для сигналов от Y-элементов вX-слой имеет вид:
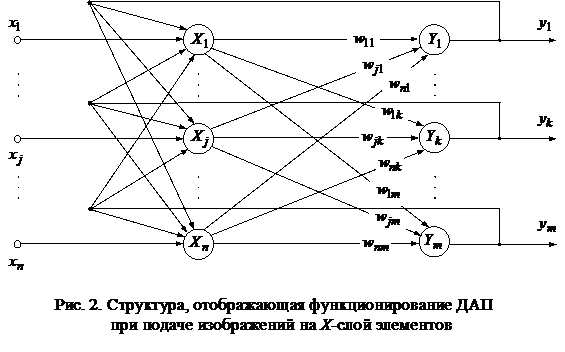
Некоторые авторы для того, чтобы подчеркнуть особенности двунаправленной ассоциативной памяти (ДАП): сходство с сетями Хопфилда, двухслойность и возможность увеличения числа слоев сети, - используют другое графическое представление архитектуры (рис. 2).
Недостаток этого графического представления ДАП состоит в том, что здесь слои нейронов находятся в неравноправном положении - создается видимость, что сеть может реагировать только при предъявлении изображений на слой X-элементов. Однако ДАП реагирует на вход каждого слоя нейронов. Как X-слой, так и Y-слой элементов может быть входным и выходным, то есть на рис. 2 или должны быть добавлены сетевые входы для Y-нейронов и сетевые выходы для X-элементов, или оговорено, что эта структура соответствует функционированию сети при подаче входного изображения на слой X?элементов.
Для биполярных нейронов элементы матрицы (1) определяются выражением
Динамика двунаправленной ассоциативной памяти является итерационной. Процесс изменения выходных сигналов нейронов каждого слоя ДАП осуществляется синхронно в начале итерации, при этом сигналы посылаются из слоя в слой последовательно, а не одновременно в обоих направлениях. При бинарных входных векторах выходные сигналы X- иY-нейронов определяются функциями активации
где
Алгоритм функционирования ДАП Шаг 1. Инициируются веса связей, определяемые с помощью соотношений (2) или (3), для множества из L пар ассоциированных друг с другом двоичных изображений Шаг 2. Для заданного изображения
Задается время t = t + 1 и вычисляются выходные сигналы X-элементов Шаг 4. До тех пор, пока не установятся выходные сигналы всех X- и Y-нейронов, выполняются шаги 5 - 7 алгоритма. Выходные сигналы Y-нейронов посылаются на входы элементов X-слоя.
Выходные сигналы X-нейронов посылаются на входы элементов Y-слоя.
то осуществляется переход к шагу 5 алгоритма, иначе - переход к шагу 8. Пример 1. Рассмотрим использование ДАП с биполярными нейронами для запоминания двух пар ассоциированных изображений В векторной форме изображения
Пусть изображения
Аналогично рассчитываются и остальные элементы матриц
Для входного изображения
то есть
Подавая вектор
При нулевых порогах X-элементов с помощью функции активации (5) рассчитывается вектор
Аналогично для изображения
где После предъявления изображений
то есть и в этих случаях сеть правильно определяет ассоциированные вектора.
2. Оценка емкости двунаправленной ассоциативной памятиКак и другие нейронные сети, ДАП имеет ограничение на максимальное количество запоминаемой информации. Если этот предел превышен, то сеть может вырабатывать неверные ассоциации. Оценки, приведенные в работе Коско, ограничивают число запоминаемых ассоциаций рассматриваемой ДАП числом m нейронов в меньшем слое при специальном кодировании изображений, максимизирующем емкость памяти. Это кодирование предусматривает получение каждого из запоминаемых изображений с одинаковыми (или отличающимися не более, чем на единицу) числами биполярных компонент с разными знаками. Более точные оценки существенно уменьшают емкость памяти нейросети. Для N случайно выбранных и оптимально закодированных векторов, каждый из которых должен быть восстанавливаемым, в общем случае необходимо выполнение неравенства
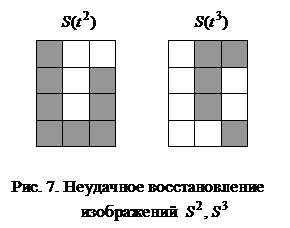
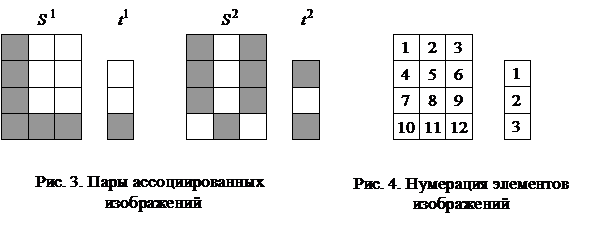
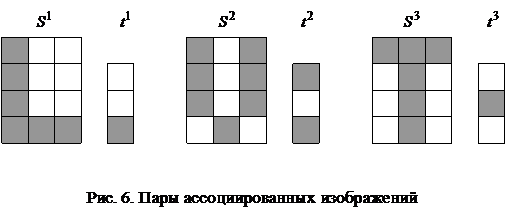
При замене требования восстановления каждого из N запоминаемых образов более слабым - восстанавливаются все запомненные вектора за исключением их незначительной части, число N может быть увеличено в два раза: Если, например, m = 1024, то число запоминаемых изображений по соотношению (6) не должно превышать 25, а по неравенству (7) - 51. Таким образом, рассмотренная ДАП может запоминать весьма ограниченное число ассоциаций. Замечание 1. Для конкретных ассоциированных пар изображений неравенства (6), (7) могут давать весьма заниженные оценки. Например, из неравенства (6) для m = 3 имеем N < 1, а из неравенства (7) следует, что N < 2, однако пример 1 убедительно показывает, что ДАП с тремя нейронами в меньшем слое запоминает и восстанавливает две ассоциации или четыре изображения, приведенные на рис. 3. Все же и в рассмотренном примере емкость ДАП невелика, уже при трех парах запоминаемых изображений (рис. 6) нейросеть не способна восстанавливать без ошибок все запомненное.
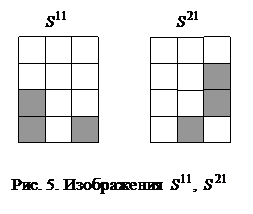
Запишем ассоциированные пары изображений
Используя векторную форму представления изображений (8) и соотношение (3) при L = 3, n = 12, m = 3, рассчитаем элементы матриц Для входных изображений
Таким образом, ДАП по предъявленным изображениям
Из выполненных вычислений следует, что по предъявленным изображениям
Требование примерного равенства чисел положительных и отрицательных биполярных компонент в каждом из запоминаемых ДАП изображений весьма существенно и его нельзя игнорировать, так как это уменьшает емкость памяти. Теоретически емкость ДАП может быть увеличена до 2m изображений, где m - число нейронов в меньшем слое, если для каждого элемента сети с биполярной функцией активацией (5) ввести свой порог q. Такая нейросеть получила название негомогенной ДАП в отличие от рассмотренной гомогенной ДАП, в которой пороги всех нейронов принимаются равными нулю. К сожалению, практическое использование негомогенной ДАП такой емкости затруднено из-за жестких ограничений, накладываемых на запоминаемые изображения. Если же изображения выбираются случайным образом, но при этом каждое из них содержит (4 + log2m) положительных биполярных компонент, а число N запоминаемых ассоциаций меньше 0,34m2/(4 + log2m), то негомогенная память может правильно восстанавливать до 98% запоминаемых изображений. При m = 1024 число запоминаемых изображений не должно превышать 3636, что на два порядка больше по сравнению с рассмотренной гомогенной ДАП. Из-за отсутствия общей теории и удобных алгоритмов для перекодирования произвольных запоминаемых наборов векторов в вектора с лимитированным числом единиц ограничение числа положительных компонент во входных изображениях является серьезным недостатком негомогенной ДАП. Другой существенный недостаток ДАП состоит в том, что при зашумленных входных векторах сеть может воспроизводить ассоциации, не соответствующие заданным входным векторам. Несмотря на эти недостатки, ДАП, в силу ее логической простоты и удобства реализации в виде СБИС, представляется очень перспективным классом интенсивно исследуемых нейросетей.
Вернуться в оглавление:Нейрокомпьютеры |
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
|
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

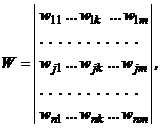 (1)
(1)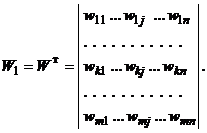
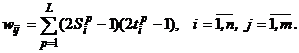 (2)
(2)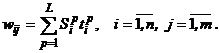 (3)
(3)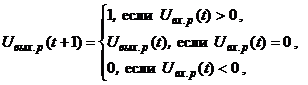 (4)
(4)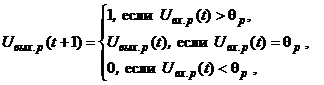 (5)
(5)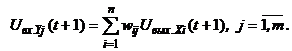
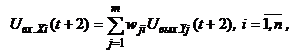
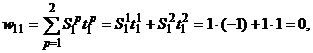
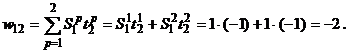
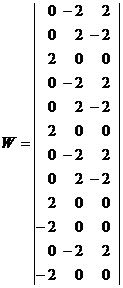 ,
, 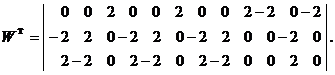
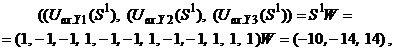
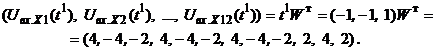
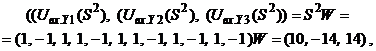
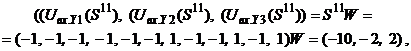
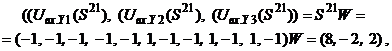
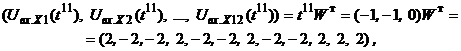
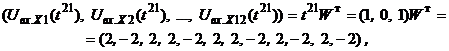
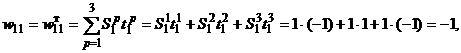
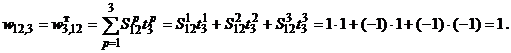
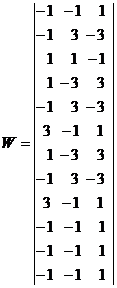 ,
,