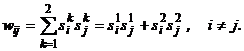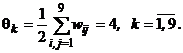|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
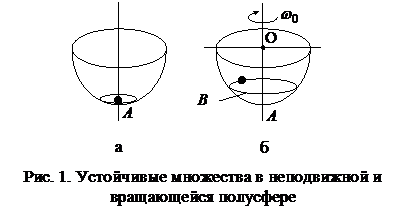
Дискретная нейронная сеть Хопфилда2.1. Нейронные сети ХопфилдаСети этого типа были предложены американским биофизиком Джоном Хопфилдом в 1982 году, когда ему удалось привлечь к анализу нейронных сетей мощный аппарат статистической физики на основе аналогий между нейронными сетями и особыми физическими системами - спиновыми стеклами. Спиновые стекла - это ансамбли электромагнитных частиц, находящихся на переходе фаз, например, нижней точке плавления стекла. Каждая частица обладает собственным моментом количества движения, называемым спином. Спин может иметь только две ориентации S1, S2 относительно внешнего магнитного поля, направленного по некоторой оси x. Одна из них совпадает с направлением поля (S1 = 1), а другая - ему противоположна (S2 = -1). Спиновые стекла обладают некоторой структурой аттракторов (устойчивых состояний) в своем фазовом пространстве. Каждый аттрактор можно рассматривать как запись определенной информации, которую можно считать при определенных условиях. Позднее выяснилось, что не только спиновые стекла, но и другие физические системы обладают в своих фазовых пространствах подходящими для нейронных сетей множествами аттракторов. Это понятие часто используется в теории нейронных сетей, поэтому приведем основные сведения об аттракторах. Если полусферу начать вращать вокруг некоторой вертикальной оси OA (рис. 1 б) с некоторой угловой скоростью w0, то шарик придет в движение и его устойчивое положение теперь будет не отдельная точка, а целая орбита B, на которую он попадает при любых бросаниях шарика внутрь этой полусферы. Если полусфера и шарик обработаны идеально и касаются друг друга только в одной точке, то точка A и траектория B превращаются в асимптотически устойчивые. Для любой окрестности (которая находится в пределах полусферы или вне ее, но обеспечивает попадание шарика в полусферу с дальнейшим движением внутри ее) точки A при неподвижной полусфере или орбиты B при вращающейся траектория шарика оканчивается в асимптотически устойчивом состоянии. Можно дать и несколько иную интерпретацию аттрактора. Представим себе некоторый природный ландшафт, когда идет сильный дождь и по местности течет вода. Аттрактору можно сопоставить озеро или бассейн, собирающий воду. А если аттрактор - это точка, через которую вода уходит под землю, то каждая капля воды стремится попасть в эту точку. Рассмотрим теперь пример из области нейронных сетей, в частности, обучение элементарного перцептрона распознаванию двух изображений, например, букв П и Г (рис. 2).
В процессе обучения сети возникают две стационарные точки или два аттрактора. Бассейны аттракторов создаются всеми изображениями букв П и Г с различными дефектами. Эти изображения совместно с эталонными многократно предъявляются перцептрону в процессе обучения сети, когда фактически по двум заданным стационарным точкам, используя итерационную процедуру, пытаются найти подходящую матрицу весов связей нейросети.
где
Определение 8. Состояние S 0, S 1, S 2, …, S k, … (3) Эта последовательность может окончиться или каким-либо стационарным состоянием S p или некоторым бесконечным динамическим процессом. В случае достижения стационарного состояния S p с некоторого момента времени t = tq наблюдаются состояния Если последовательность (3) не оканчивается стационарным состоянием, то есть бесконечна, то в общем случае при случайном срабатывании отдельных нейронов или их групп возникают трудно анализируемые последовательности (3) состояний сети. В связи с этим ограничимся только режимами срабатывания, которые однозначно определяют следующее состояние сети по текущему. Одним из таких режимов является режим синхронного срабатывания всех элементов сети (режим маршировки), другим - режим последовательного или циклического срабатывания по одному элементу: i-й, (i + 1)-й, …, n-й, …, 1-й, 2-й, …, i-й, (i + 1)-й, … . При этих режимах срабатывания нейронов цепочка состояний (3.) однозначно определяется своим начальным состоянием S 0. В силу конечного числа n двоичных элементов сети конечно и общее число (2n) состояний нейросети, поэтому в бесконечной последовательности (3) найдутся по крайней мере два одинаковых состояния то есть цикл повторяется. В частном случае, когда p = q + 1, получаем одночленный цикл или рассмотренное выше стационарное состояние. а объединение бассейнов всех циклов равно множеству всех состояний S нейронной сети:
Точки цикла, имеющие непустые деревья, называются точками входа в цикл. Деревья разных точек входа не пересекаются, а их совокупность покрывает весь бассейн аттрактора. Каждое состояние
В худшем случае, когда цикл имеет одну точку входа, а дерево линейно, высота дерева равна числу состояний сети в бассейне аттрактора.
Если соотношения (4) выполняются не для всех циклов Ci, то сети считаются несравнимыми. Высота деревьев бассейнов аттракторов используется и для оценки качества процессов или алгоритмов обучения. Пусть имеется два алгоритма обучения A1,A2, которые по заданным стационарным состояниям S сети получают матрицы весов связей WA1(S), WA2(S). Если бассейны аттракторов, порожденные матрицей весов WA1(S) получаются регулярно (быть может, с редким исключением) лучше бассейнов нейросетей с матрицей WA2(S), то алгоритм обучения A1 лучше алгоритма A2.
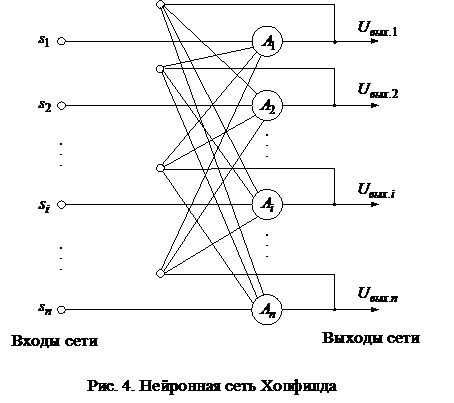
2. Дискретная сеть ХопфилдаВ своей первой работе, посвященной нейронным сетям, Хопфилд рассмотрел полносвязную нейронную сеть из бинарных элементов с симметричными связями. Структура этой сети приведена на рис. 4.
Дискретная сеть Хопфилда состоит из единственного слоя нейронов, каждый из которых связан со всеми остальными и имеет сетевые вход и выход. Сигналы на сетевых входах нейронов определяют их выходные сигналы:
При отсутствии сигналов на сетевых входах элементы сети функционируют в асинхронном режиме, при котором каждый из них определяет свой выходной сигнал в случайные моменты времени с заданной средней частотой в соответствии с выражением
Такой вид матрицы весов обеспечивает устойчивость сети: при подаче на ее входы внешних сигналов возникает последовательность состояний сети вида (3), которая оканчивается стационарным состоянием. Процесс достижения стационарного состояния можно описать с помощью минимизации специальной энергетической функции:
где E - искусственная энергия сети, заданная в виде функции Ляпунова; Uвх.j - внешний входной сигнал j-го нейрона. Из выражений (8) и (7) имеем:
Рассмотрим изменение энергии DEj произвольного j-го элемента при его срабатывании:
Для бинарных нейронов приращения их выходных сигналов может принимать только три значения: +1, 0, -1. При этом знак приращения DUвых.j для j-го элемента совпадает со знаком выражения в круглых скобках. Действительно, если DUвых.j = -1, то есть нейрон переходит из единичного состояния в нулевое, то это означает, что в соответствии с выражением (5) выполняется неравенство
Из совпадения знаков сомножителей в выражении (9) следует, что при срабатывании любого j-го нейрона ни его энергия, ни энергия всей сети увеличиться не может. Она либо остается прежней, если DUвых.j = 0, либо уменьшается, если DUвых.j ? 0. Следовательно, по мере срабатывания нейронов энергия будет монотонно убывать, пока не достигнет одного из своих локальных минимумов, которому соответствует одна из стационарных точек нейросети. Эволюция сети из любого начального состояния в силу существования функции Ляпунова (7) всегда кончается в одной из ее стационарных точек, то есть аттракторами в дискретной бинарной сети Хопфилда являются только стационарные точки. Это же утверждение справедливо и для дискретной сети Хопфилда с биполярными нейронами. Для хранения некоторого множества изображений где индекс k указывает на принадлежность входных сигналовk-му изображению.
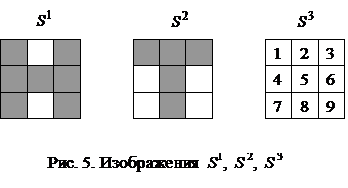
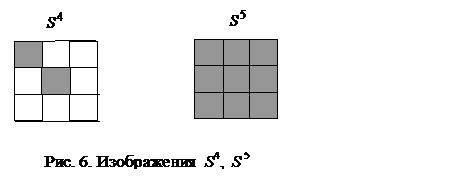
Пороги qi всех бинарных элементов обычно принимаются равными нулю, а пороги биполярных нейронов часто определяются через сумму элементов матрицы весов: Для сети Хопфилда число p запоминаемых изображений не должно превышать величины, примерно равной 0,15n, где n - число нейронов сети. Кроме того, если есть пары очень похожих изображений, например, S k,S q, то они могут вызывать у сети перекрестные ассоциации, то есть предъявление на входы сети изображения S k может приводить к появлению на ее выходе изображения S q и наоборот. Задачи, решаемые дискретной сетью Хопфилда с бинарными или биполярными нейронами в качестве ассоциативной памяти, формулируются следующим образом. Известен набор эталонных двоичных изображений или сигналов. Сеть должна уметь по частичной информации неидеальных изображений, подаваемых на ее вход, выделять эталонные изображения или давать информацию о том, что входной вектор не соответствует ни одному из хранимых в ее памяти. Когда сеть распознает какое-либо изображение, то на ее выходах появляется именно это изображение. В противном случае вектор выходных сигналов не совпадает ни с одним из эталонных. Пример 1. Рассмотрим возможности дискретной сети Хопфилда с девятью биполярными нейронами по распознаванию неидеальных изображений букв Н и Т. Эталонные изображения S1и S2 этих букв приведены на рис. 5, там же дана нумерация элементов изображений, соответствующая нейронам сети Хопфилда и их векторному представлению:
В соответствии с исходными данными выражение (11) для рассматриваемого примера принимает вид:
Рассчитаем вес связи w12: w12 = 1? (-1) + 1?1 = 0. В силу общего равенства
Пороги биполярных нейронов сети Хопфилда рассчитываются с помощью соотношения (12) и данных табл. 1:
Предъявим сети Хопфилда изображение S 1 буквы Н (рис. 5) и рассчитаем выходные сигналы сети после его снятия при двух значениях порогов: Таблица 2. Результаты расчетов выходных сигналов сети Хопфилда после
Из анализа данных табл. 2 следует, что вектор выходного изображения сети повторяет изображение S 1 в широком диапазоне значений порогов. Аналогичная ситуация получается и при предъявлении изображения S 2 буквы Т (табл. 3), то есть рассчитанная дискретная сеть Хопфилда, как ей и положено, повторяет на своем выходе идеальные входные изображения. Таблица 3. Результаты расчетов выходных сигналов сети Хопфилда после
Предъявим теперь сети изображение S 3И, инверсное изображению S 3 (рис. 5). Изображение S 3И можно рассматривать как искаженное представление буквы Н, у которого утеряны две отрицательные компоненты. Результаты расчетов для этого случая при Таблица 4. Результаты расчетов выходных сигналов сети Хопфилда после
При предъявлении изображений S 1, S 2, S 3И сеть попадала в стационарную точку за один такт времени при синхронном срабатывании всех ее элементов. Однако такое идеально быстрое достижение устойчивого состояния возможно далеко не всегда. Предъявим сети изображение S 4 (рис. 6), которое можно рассматривать как сильно искаженный эталон буквы Н, у которого пять единичных компонент заменены на противоположные "-1". Для достижения стационарной точки, соответствующей изображению S 1 буквы Н, в этом случае при
Таблица 5. Результаты расчетов выходных сигналов сети Хопфилда после
Вернуться в оглавление:Нейрокомпьютеры |
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |


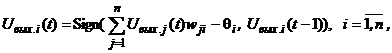 (1)
(1)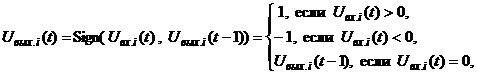 (2)
(2)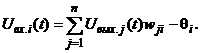

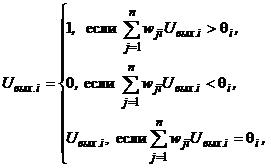 (5)
(5)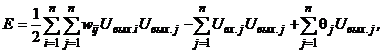 (7)
(7)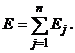 (8)
(8)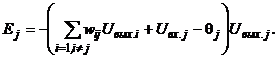
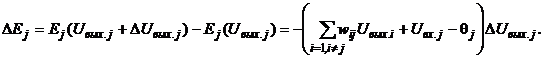 (9)
(9)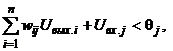
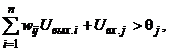
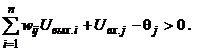
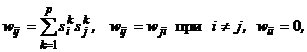 (10)
(10)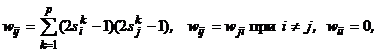 (11)
(11)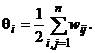 (12)
(12)