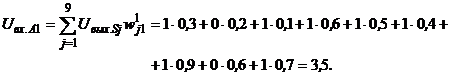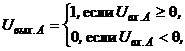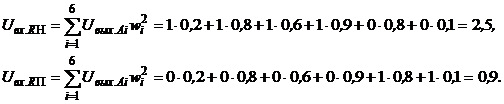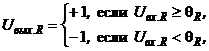|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
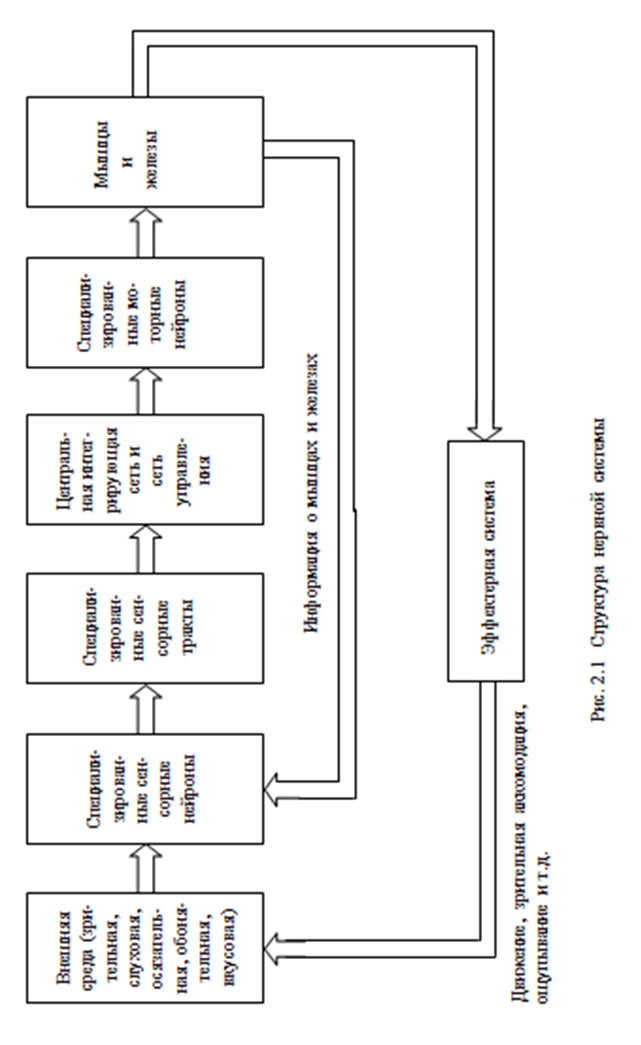
Элементарный перцептрон Розенблатта1. Перцептроны – класс моделей мозгаПерцептроны или персептроны (от perceptio – восприятие) были первыми искусственными нейронными сетями, появившимися в результате многолетних исследований мозга животных и человека. Автор первого перцептрона – американский ученый Френк Розенблатт, впервые опубликовавший свои исследования в этой области в 1957 году. По мнению Ф. Розенблатта, перцептроны, прежде всего, являются классом моделей мозга, объясняющих некоторые его характерные функции. В частности, перцептроны, пусть и в самой элементарной форме, объясняют некоторые проблемы организации памяти биологических систем, демонстрируют механизм приобретения знаний «познающих (cognitive) систем» об окружающем их мире и показывают, что эти знания зависят как от когнитивной системы, так и от окружающей среды. По Розенблатту, для различных видов животных простейшее представление об анатомической структуре нервной системы может быть получено с помощью схемы, представленной на рис. 2.1. Каждый из пяти видов информации о внешней среде воспринимается своими специализированными сенсорными нейронами и передается по своим отдельным сенсорным трактам в центральную нервную систему. Через моторные нейроны центральная нервная система связана с мышцами и железами организма. В своих первых работах Розенблатт рассматривал модель только зрительной системы. В наиболее простом виде эта модель включает в себя три последовательно соединенных множества нейронов: чувствительных (S-элемен-тов), ассоциирующих (A-элементов) и реагирующих (R-элементов). S-элементам в нервной системе животного или человека соответствуют сенсорные или рецепторные нейроны, генерирующие сигналы на поступающие внешние раздражения (изображения) и передающие их A-нейронам. A-элементы аналогичны в нервной системе живого организма нейронам, образующим локальный специализированный зрительный центр в коре головного мозга и связывающим рецепторные нейроны с моторными. R-элементам в нервной системе соответствуют эффекторные (моторные) нейроны, упорядоченные в ограниченные топологические структуры и передающие сигналы управления центральной нервной системы к мышцам и железам организма.
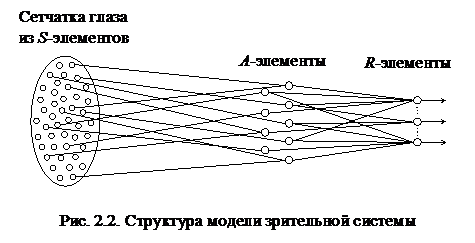
Определение 2.3. Простым биполярным (бинарным) реагирующим элементом называется R-элемент, выдающий единичный выходной сигнал, если алгебраическая сумма его входных сигналов больше или равна пороговому значению, и отрицательный единичный (нулевой) сигнал, если сумма его входных сигналов меньше заданного порога. Чувствительные S-элементы живого организма (рис. 2.2) возбуждаются от воздействия энергии света, если величины их входных сигналов превышают некоторый порог
Комбинация выходов всех A-элементов представляет собой реакцию двух первых слоев перцептрона на предъявленное входное изображение, которая с помощью выходного слоя нейронов преобразуется в необходимую комбинацию выходных сигналов системы. Часто требуют, чтобы каждому классу входных изображений соответствовал только один определенный активный R-нейрон. Необходимых комбинаций выходных сигналов на каждый класс изображений добиваются на этапе обучения или адаптации перцептрона за счет изменения переменных весов связей между A- и R-элементами. Определение 2.4. Простым перцептроном называется нейронная сеть, состоящая из S-, A- и R-элементов и удовлетворяющая следующим пяти условиям:
где wij(t) – вес связи между i-м и j-м нейронами в момент времени t;
2. Обучение перцептронов с помощью a- и g-систем подкрепленияОпределение 2.7. Системой подкрепления нейронной сети называется любой набор правил, с помощью которых можно изменять во времени состояние памяти сети (или матрицу взаимодействия). Определение 2.8. Положительным (отрицательным) подкреплением назы-вается такой процесс коррекции весов связей, при котором вес связи wij(t), начи-нающейся на выходе активного i-го элемента и оканчивающейся на входе j-го элемента, изменяется на величину ?wij(t), знак которой совпадает со знаком выходного сигнала j-го нейрона (знак которой противоположен знаку выходного сигнала j-го нейрона).
где R* – желаемая реакция; R – полученная реакция; f(0) = 0. Конкретным примером системы подкрепления с коррекцией ошибок является альфа-система подкрепления. В этой системе при наличии ошибок веса всех активных связей, которые оканчиваются на R-элементе, изменяют на одинаковую величину ?, а веса всех неактивных связей оставляют без изменений. Перцептроны, в которых применяется альфа-система подкрепления, называются альфа-перцептронами. При использовании альфа-системы подкрепления сумма весов всех связей между R- и A-нейронами может возрастать (или убывать) от шага к шагу, что должно приводить к нежелательным ситуациям, когда многие связи имеют максимальные (или минимальные) веса и не могут использоваться в дальнейшем процессе обучения нейронной сети. Для устранения этого недостатка ?-системы подкрепления была предложена гамма-система подкрепления, которая обладает свойством консервативности относительно суммы ?1 весов всех связей между нейронами, т.е. сумма ?1 остается постоянной в процессе обучения перцептрона. Это достигается за счет того, что при наличии ошибочной реакции перцептрона сначала веса всех активных связей изменяются на одинаковое значение ?, а вслед за этим из весов всех активных и пассивных связей вычитается величина, равная отношению суммы изменения весов всех активных связей к числу всех связей. Изменение весов отдельных связей при этом определяется соотношением: где ?wij – в общем случае приращение веса связи между i-м A-нейроном и j-м R-нейроном, для элементарного перцептрона j = const = 1; ? – величина сигнала подкрепления; Nак – число активных связей; N – число связей, оканчивающихся на входе j-го элемента. из которого и следует консервативность гамма-системы подкрепления относи-тельно суммы весов всех обучаемых связей.
Если неравенства (2.3) нарушаются, а требование консервативности относительно суммы ?1 весов связей остается неизменным, то соотношение (2.2) необходимо уточнить. Пусть, например, среди активных связей Nа гр. связей имеют граничные значения весов Пусть также Nа бгр. активных связей имеют веса, близкие к граничным, для которых справедливы неравенства
В этом случае общая сумма Sa первоначальных изменений весов активных связей будет равна:
Если предположить, что для всех пассивных связей выполняются соотношения (2.3), тогда из весов пассивных связей и весов активных связей, для которых не выполняется соотношение (2.4) или (2.5), вычитается величина
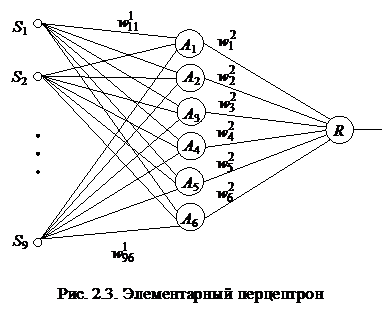
Примером еще одного общего способа обучения перцептронов является метод коррекции ошибок случайными возмущениями. Он предусматривает, как и альфа-система подкрепления, при появлении ошибок – коррекцию весов активных связей, но знак и величина коррекции для каждой связи выбирается случайно в соответствии с некоторым заданным распределением вероятностей. Пример 2.1. Выполним обучение элементарного перцептрона с бинарными S- и A-нейронами и биполярным R-нейроном (рис. 2.3) распознаванию изображений букв Н и П (рис. 2.4 а, б) на рецепторном поле из девяти элементов (рис 2.4 в). При этом потребуем, чтобы при предъявлении изображения буквы Н на выходе R-элемента был сигнал “–1”, при появлении второго изображения – сигнал “+1”.
а б в Рис 2.4. Изображения букв Н и П Зададим в таблицах 2.1 и 2.2 веса связей Таблица 2.1. Веса
Таблица 2.2. Веса
Подадим на вход перцептрона изображение буквы Н (рис 2.4 а). Это изображение возбуждает все S-нейроны, кроме второго и восьмого. Единичные сигналы с выходов возбужденных бинарных S-нейронов через связи, весовые коэффициенты которых заданы табл. 2.1, поступают на входы А-нейронов. Суммарный входной сигнал на входе i-го А-элемента определяется соотно-шением: где
Аналогично вычисляются сигналы на входах остальных А-элементов. Результаты этих вычислений приведены во второй строке табл. 2.3. В третьей строке этой таблицы – результаты расчетов сигналов на входах А-элементов при предъявлении перцептрону изображения буквы П. Таблица 2.3. Величины сигналов на входах A-элементов
Для упрощения расчетов положим, что пороги Если величина порога Пусть выходной сигнал А-элементов определяется соотношением При величине порога R-элемента Таблица 2.4. Адаптация весов связей перцептрона с помощью
Во втором столбце таблицы при t=t0 приведены значения исходных весов связей и величины сигналов где
а для приращений весов пассивных связей имеем:
Зная приращения весов связей и используя соотношение:
Таблица 2.5. Адаптация весов связей перцептрона с помощью
При предъявлении изображения буквы П в момент времени
Вернуться в оглавление:Нейрокомпьютеры |
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

 (2.2)
(2.2)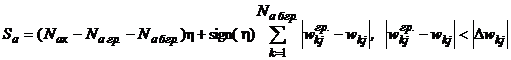 , (2.6)
, (2.6)
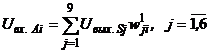 , (2.8)
, (2.8)