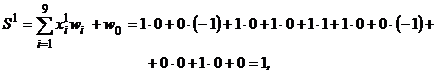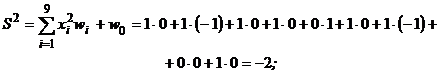|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
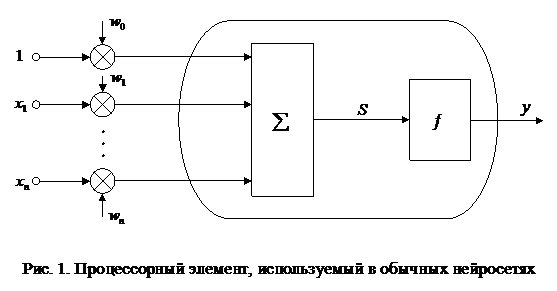
Нейронная сеть Хебба1.Формальные нейроны искусственных нейронных сетей При моделировании нейронных сетей в качестве искусственных нейронов обычно используется простой процессорный элемент, изображенный на рис. 1. На его входы поступает вектор Х = (х1, …, хп) входных сигналов, являющихся выходными сигналами других нейронов, а также единичный сигнал смещения. Все входные сигналы, включая и сигнал смещения, умножаются на весовые коэффициенты своих связей и суммируются: где S – суммарный входной сигнал; wi (
Полученный сигнал S поступает на вход блока, реализующего функцию f активации нейрона. Типичными функциями активации являются бинарная
или биполярная
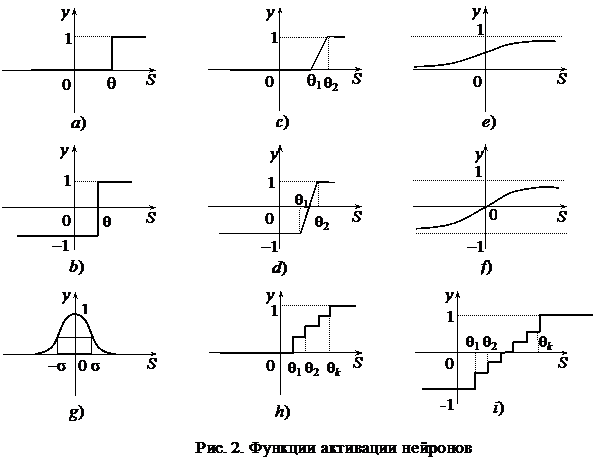
где Графическое изображение бинарной и биполярной функций активации для этого случая представлено на рис. 2а и 2b.
где а равно нулю для бинарных выходных сигналов нейронов и а равно минус единице для биполярных сигналов; k, a0 - постоянные коэффициенты.
где ? – постоянный коэффициент;
радиально-симметричная (рис.2g):
К-значная бинарная (рис.2h): К-значная биполярная (рис.2i):
Приведенные модели искусственных нейронов игнорируют многие известные свойства биологических прототипов. Например, они не учитывают временные задержки нейронов, эффекты частотной модуляции, локального возбуждения и связанные с ними явления подпороговой временной и пространственной суммации, когда клетка возбуждается не одновременно пришедшими импульсами, а последовательностями возбуждающих сигналов, поступающих через короткие промежутки времени. Не учитываются также периоды абсолютной рефрактерности, во время которых нервные клетки не могут быть возбуждены, т.е. как бы обладают бесконечно большим порогом возбуждения, который затем за несколько миллисекунд после прохождения сигнала снижается до нормального уровня. Этот список отличий, которые многие биологи считают решающими, легко продолжить, однако искусственные нейронные сети все же обнаруживают ряд интересных свойств, характерных для биологических прототипов.
2. Решение задач распознавания на основе отдельных нейронов. Правило Хебба Искусственные нейронные сети, предназначенные для решения разнообразных конкретных задач, могут содержать от нескольких нейронов до тысяч и даже миллионов элементов. Однако уже отдельный нейрон (рис. 1) с биполярной или бинарной функцией активации может быть использован для решения простых задач распознавания и классификации изображений. Выбор биполярного (1, –1) или бинарного (1, 0) представления сигналов в нейросетях осуществляется исходя из решаемой задачи и во многих случаях он равноценен. Имеется спектр задач, в которых бинарное кодирование сигналов более удобно, однако в общем биполярное представление информации более предпочтительно. то выходной сигнал у = 1 и, следовательно, входное изображение X ? принадлежит классу X 1. Если S ? 0, то у = –1 и предъявленное изображение при-надлежит второму классу. x1w1 + x2w2 + … + xnwn+w0 = 0. Для двумерных входных векторов границей между двумя классами изображений является прямая линия: входные вектора, расположенные выше этой прямой, принадлежат к одному классу, а ниже – к другому. wi (t + 1) = wi (t) + xi у, где wi (t), wi(t + 1)соответственно вес i-й связи нейрона до и после адаптации; xi ( wi = 0, Шаг 2. Для каждой пары(X k, t k), Шаг 3. Инициируется множество входов нейрона:
x0 = 1, xi = xik,
Шаг 4. Инициируется выходной сигнал нейрона: y =t k. Шаг 5. Корректируются веса связей нейрона по правилу
Шаг 6. Проверка условий останова. Для каждого входного изображения X k рассчитывается соответству-ющий ему выходной сигнал y k:
где Если вектор (y1, …, ym) рассчитанных выходных сигналов равен вектору (t1, …, tm) заданных сигналов нейрона, т.е. каждому входному изображению соответствует заданный выходной сигнал, то вычисления прекращаются (переход к шагу 7), если же (y1, …, ym) ??(t1, …, tm), то переход к шагу 2 алгоритма.
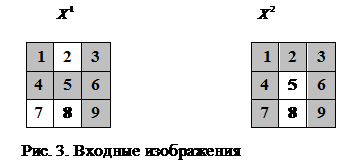
М = {(Х 1 = (1, –1, 1, 1, 1, 1,–1, –1, 1), 1), инициируются веса связей нейрона: wi = 0, Шаг 5. Корректируются веса связей нейрона по правилу Хебба
Шаг 3. Инициируется множество входов нейрона для изображения Х 2 второй пары: х0 = 1, хi = хi2, Шаг 5. Корректируются веса связей нейрона:
Шаг 6. Проверяются условия останова. Рассчитываются входные и выходной сигналы нейрона при предъявлении изображения X 1:
y1 = 1, так как S1 > 0. Рассчитываются входной и выходной сигналы нейрона при предъявлении изображения Х 2
y2 = –1, так как S2 < 0. Поскольку вектор (y1, y2) = (1, –1) равен вектору (t1, t2), то вычисления прекращаются, так как цель достигнута – нейрон правильно распознает заданные изображения. Основная идея правила (13) – усиливать связи, которые соединяют нейроны с одинаковой по времени активностью, и ослаблять связи, соединяющие элементы с различной активностью, может быть использована и при настройке нейросетей с бинарными элементами. Правило Хебба (13) для однослойных бинарных сетей можно записать в виде: wi (t + 1) = wi (t) + Пример 2. Пусть требуется обучить бинарный нейрон распознаванию изображений Х 1и Х 2 примера 1. При этом изображению Х 1 пусть соответствует выходной сигнал нейрона “+1”, а изображению Х?2 – “0”. Применение правила Хебба в этом случае дает следующие результаты: Шаг 1. Задается множество М = {(Х?1 = (1, 0, 1, 1, 1, 1, 0, 0, 1), 1), (Х?2 = ( 1, 1, 1, 1, 0, 1, 1, 0, 1 ), 0)}, и инициируются веса связей нейрона wi = 0, Шаг 4. Инициируется выходной сигнал нейрона для изображения Х1: у = t1 = 1. Шаг 5. Корректируются веса связей нейрона с помощью соотно-шений (14), (15):
Шаг 3. Инициируется множество входов нейрона элементами изоб-ражения Х 2: Шаг 4. Инициируется выходной сигнал нейрона для изображения Х 2: Шаг 5. Корректируются веса связей нейрона с помощью соотно-шений (14), (15):
Шаг 6. Проверка условий останова. Рассчитываются входные и выходные сигналы нейрона при предъ-явлении изображений Х 1, Х 2:
y1 = 1, так как S1 > 0. y2 = –1, так как S 2 < 0. Поскольку вектор (y1, y2)= (1, 0) равен заданному вектору (t1, t2) = = (1, 0), то цель достигнута и вычисления прекращаются.
3. Нейронная сеть ХеббаИспользование группы из m биполярных или бинарных нейронов A1, …, Am (рис. 4) позволяет существенно расширить возможности нейронной сети и распознавать до 2m различных изображений. Правда, применение этой сети для распознавания 2m (или близких к 2m чисел) различных изображений может приводить к неразрешимым проблемам адаптации весов связей нейросети. Поэтому часто рекомендуют использовать данную архитектуру для распознавания только m различных изображений, задавая каждому из них единичный выход только на выходе одного А-элемента (выходы остальных при этом должны принимать значение “–1” для биполярных нейронов или “0” – для бинарных).
Однослойная нейронная сеть с двоичными нейронами, приведенная на рис.4, может быть обучена с помощью алгоритма на основе правила Хебба. В этом случае она называется сетью Хебба. Использование других алгоритмов обучения этой же сети приводит и к изменению названия нейронной сети. Использование в названии сетей их алгоритмов обучения характерно для теории нейронных сетей. Для биполярного представления сигналов возможно обучение нейросети с помощью следующего алгоритма: wji = 0,
Шаг 6. Проверяются условия останова, т.е. правильности функциониро-вания сети при предъявлении каждого входного изображения. Если условия не выполняются, то переход к шагу 2 алгоритма, иначе – прекращение вычислений (переход к шагу 7).
Вернуться в оглавление:Нейрокомпьютеры |
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
|
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

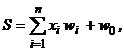 (1)
(1)
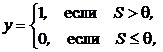 (4)
(4)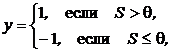 (5)
(5)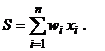 (6)
(6)
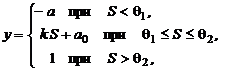 (7)
(7)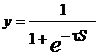 , (8)
, (8)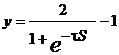 , (9)
, (9)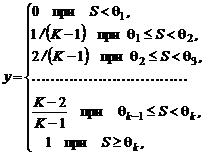 (11)
(11)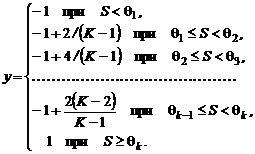 (12)
(12)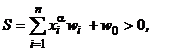
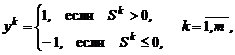
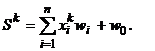
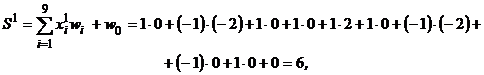
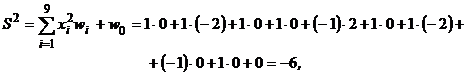
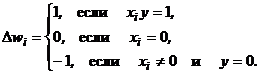 (15)
(15)