Разработка математической модели

Функционирование системы заключается в выполнении технологического процесса. При этом в системе одновременно протекает несколько технологических процессов. Технологический процесс представляет собой определенную последовательность отдельных операций. Часть операций может выполняться параллельно разными активными ресурсами системы. Задается технологический процесс одним из способов представления алгоритмов.

В системах с программным принципом управления, обеспечивающих параллельное выполнение нескольких технологических процессов, имеются алгоритмы управления совокупностью процессов. Основное назначение таких алгоритмов заключается в разрешении конфликтных ситуаций, возникающих, когда два или более процесса претендуют на один и тот же ресурс. Совокупность алгоритмов управления 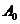 совместно с параметрами входных воздействий  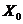и компонентов  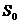описывают динамику функционирования системы. Обычно алгоритмы управления представляются в виде  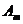удобном для моделирования. Данный подход к описанию динамики работы системы наиболее удобен для имитационного моделирования и является естественным способом определения характеристик системы:
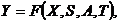                                               (1)
где 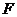 множество операторов определения выходных характеристик,
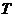– календарное время моделирования.

Для систем со структурным принципом управления получил распространение другой подход к описанию динамики работы системы. Для каждого компонента выбирается определенный параметр 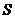 или несколько параметров, значения которых изменяются в ходе функционирования компонента и отражает его состояние в текущий момент времени 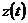. Множество таких параметров по всем  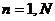элементам системы  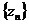отражает состояние системы 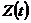. Функционирование системы представляется в виде последовательной смены состояний: 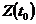, 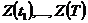. Множество  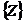возможных состояний системы называют пространством состояний. Текущее состояние системы в момент времени  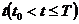отражается в виде координаты точки в 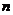– мерном пространстве состояний, а вся реализация процесса функционирования системы за время 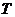– в виде некоторой траектории [1].
При заданном начальном состоянии системы 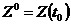 можно определить ее состояние в любой момент  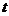из интервала 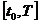, если известна зависимость
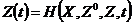.                (2)
В этом случае выходные характеристики системы определяются по выражению
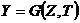.                            (3)
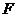В выражениях (1), (3) операторы  и 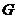 называют операторами выходов, а в (2) оператор  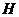– оператором переходов. С целью перевода обобщенной модели в форме (1) или в форме (1), (3) в конструктивную необходимо конкретизировать свойства множеств переменных и операторов. Для определенных классов систем разработаны формализованные схемы и математические  методы, которые позволяют описать функционирование системы, а в некоторых случаях – выполнить аналитические исследования.
Одной из наиболее общих формализованных схем является описание в виде агрегативных систем [3]. Этот метод в наибольшей мере приспособлен для описания систем, у которых характерно представление входных и выходных воздействий в виде ”сообщений”, составленных из совокупностей “сигналов”. В основе метода лежит понятие агрегата как компонента системы. Математическая модель агрегата выражается в виде зависимостей (2), (3) с конкретизацией входных воздействий, состояний и операторов переходов и выходов. Единообразное математическое описание исследуемых объектов в виде агрегативных систем позволяет использовать универсальные средства  имитационного моделирования.

Для описания стохастических систем с дискретными множествами состояний, входных и выходных воздействий, функционирующих в непрерывном времени, широко используются стохастические сети. Стохастическая сеть представляет собой совокупность систем массового обслуживания, в которой циркулируют заявки, переходящие из одной системы в другую.

Если в модели системы не учитывается воздействие случайных факторов, а операторы переходов и выходов непрерывны, то зависимости (2), (3) могут быть представлены в виде дифференциальных уравнений


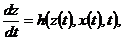
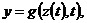
где 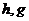 – вектор–функции состояний ее выходов соответственно;
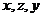       – векторы входных воздействий, состояний и выходных воздействий соответственно.
Системы состояния которых определены в дискретные моменты времени 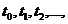 получили название автоматов. Если за единицу времени выбран такт  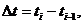то дискретные моменты времени принимаются в виде 0,1,2,… [3]. В каждый дискретный момент времени, за исключением 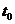, в автомат поступает входной сигнал 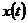, под действием которого автомат переходит в новое состояние в соответствии с функцией переходов

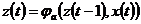
и выдает выходной сигнал, определяемый функцией выходов

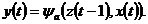
Если автомат характеризуется конечными множествами состояний 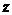, входных сигналов 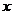, и выходных сигналов 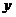, он называется конечным автоматом. Функции переходов и выходов конечного автомата задаются таблицами, матрицами или графиками.
Стохастические системы, функционирующие в дискретном времени, можно представлять вероятностными автоматами. Функция переходов вероятностного автомата определяет не одно конкретное состояние, а распределение вероятностей на множестве состояний, а функция выходов – распределение вероятностей на множестве выходных сигналов. Функционирование вероятностных автоматов изучается при помощи аппарата цепей Маркова. Для анализа систем, представляемых в виде автоматов, могут использоваться аналитические или имитационные методы.

В классе автоматов для исследования систем, функционирование которых описывается совокупностью параллельных взаимодействующих процессов, широко используются сети Петри и их различные модификации, сети Керка, Е – сети.