Рассмотрим следующую группу характеристик, получение которых основывается на вычислении t-инвариантов (или t-циклов).
Целочисленный вектор У называется t-инвариантом, если он является решением линейной системы.
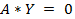(13)
Если значение t-инварианта подставить в уравнение (6) вместо вектора счёта срабатываний S, то окажется, что
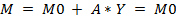
Отсюда следует, что если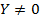 
, то сеть устойчива, т. е. после ряда переключений она возвращается в исходное состояние M0. Устойчивость процессов связана с их циклической повторяемостью, начиная с состояния M0. заметим, что среди решений системы (13) могут быть такие векторы У, компоненты yi которых отрицательны.
Полная t-цепь – это t-цикл, все компоненты которого положительны. Полная t-цепь включает в себя все переходы сети. Если сеть имеет полную t-цепь, то она жива при любом начальном маркировании, поскольку в цепи маркирований от M0 до М= M0 срабатывают все переходы.
Таким образом, по устойчивости процессов и значению t-инварианта можно определить живость сети: если сеть жива и ограничена, то она инвариантна и устойчива.
