Статистические модели

В тех случаях, когда отношения в объекте трудно установить из-за их многообразия, сложности и невыясненной природы процессов, используются статистические методы для математического выражения зависимостей между характеристиками и параметрами объекта. Сущность статистических методов состоит в следующем. На основе эмпирических представлений о свойствах исследуемого объекта и в соответствии с целью исследования определяется состав признаков, характеризующих объект, и тип статистической модели (математические выражения, структуры). Признаками, посредством которых описывается объект, являются величины, соответствующие параметрам 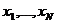 и характеристикам  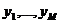объекта. Наблюдением (измерения, регистрация) собираются статистические данные, образующие выборку 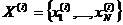, , 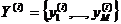где 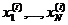,  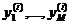– значения признаков при  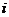–м наблюдении, .

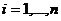Математическая статистика предлагает обширный набор моделей и методов установления статистических закономерностей, присущих исследуемым объектам. Наиболее широкое применение получил регрессионный анализ.

Регрессионный анализ состоит в построении функций 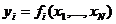, связывающих характеристики (зависимые переменные) с параметрами (независимыми переменными), на основе статистической выборки, содержащей статистически независимые данные. Статистическая независимость данных состоит в том, что значения признаков разных наблюдений статистической выборки не должны зависеть друг от друга. Чтобы проявились статистические зависимости, число наблюдений должно превосходить число признаков в 6–8 раз. Выборка должна быть однородной, то есть относиться к объектам одного класса.

Зависимость характеристики от параметров 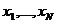 представляется в виде линейного полинома

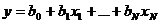
а при необходимости – в виде полинома более высокого порядка
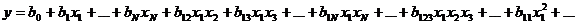         Параметры  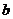называются коэффициентами регрессии. Если число признаков 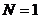, то имеет место уравнение парной регрессии, при  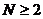– уравнение множественной регрессии. Переменная  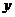рассматривается как случайная величина, которая распределена в окрестности среднего значения 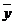, зависящего от  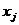то есть считается, что переменные  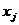влияют лишь на среднее значение 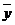. Коэффициенты регрессии оцениваются по методу наименьших квадратов минимизацией дисперсии отклонения уравнения регрессии от наблюдаемых значений , .
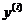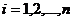При построении регрессионной модели основными являются два момента:

1. выбор числа независимых признаков ;
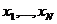2. выбор формы полинома, посредством которого представляется зависимость .

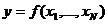Процедуры оценки качества и улучшения моделей реализованы в пакетах прикладных программ статистического анализа.
Регрессионные модели обладают следующими особенностями:

1. они применимы для прогноза значений 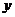 только при аргументах 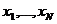, принадлежащих области определения переменных, для которой построено уравнение регрессии;
2. уравнения регрессии принципиально необратимы, то есть недопустимо путем тождественных преобразований из уравнения 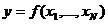 строить уравнение 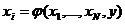,поскольку это две совершенно различные регрессии, каждая из которых должна строиться самостоятельно;
3. регрессионные модели не раскрывают механизм взаимосвязи характеристик и параметров и фиксируют лишь количественную взаимосвязь величин.

Регрессионные и другие статистические модели наиболее широко используются для описания рабочей нагрузки, создаваемой прикладными задачами, а также системными процессами (управление заданиями, задачами, данными, ввод–вывод и др.).

Применение статистических методов для этого класса объектов объясняется тем, что хотя рабочая нагрузка, как правило, хорошо наблюдаема, однако по своей природе – это чрезвычайно сложный объект. В нем совмещены свойства прикладных задач, технология обработки данных, организация операционной системы и даже конфигурация ЭВМ, для которой разрабатывается программное обеспечение. Поэтому рабочую нагрузку приходится рассматривать как черный ящик и описывать количественные взаимосвязи статистическими методами.

Регрессионные модели применяются также для компактного представления и анализа зависимостей, воспроизводимых на имитационных моделях.