Моделирование на ЭВМ и анализ результатов моделирования

Обработка измерений имитационного моделирования

При статистическом моделировании в ходе имитационного эксперимента измеряются множества значений по каждой выходной характеристике. Эти выборки необходимо обрабатывать для удобства последующего анализа и использования. Поскольку выходные характеристики зачастую являются случайными величинами или функциями, обработка заключается в вычислении оценок математических ожиданий, дисперсий и корреляционных моментов.

Для того, чтобы исключить необходимость хранения в машине всех измерений, обработку проводят по рекуррентным формулам, когда оценки вычисляют в процессе эксперимента методом нарастающего итога по мере появления новых измерений.

Для стохастических характеристик можно построить гистограмму относительных частот – эмпирическую плотность распределения. С этой целью область предполагаемых значений характеристики 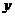 разбиваются на интервалы. В ходе эксперимента по мере измерений определяют число попаданий характеристики в каждый интервал и подсчитывают общее число измерений. После завершения эксперимента для каждого интервала вычисляют отношение числа попаданий характеристики к общему числу измерений и длине интервала.

Для случайных нестационарных характеристик период моделирования 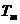 разбивается на отрезки  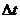и запоминаются значения характеристики в конце каждого 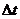. Проводится серия экспериментов с разными последовательностями случайных параметров модели. Измерения по каждому  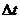обрабатываются как при оценке случайных величин.

Определение зависимостей характеристик от параметров системы

Для анализа зависимостей характеристик от параметров системы и внешних воздействий можно воспользоваться корреляционным, дисперсионным или регрессионным методами.

С помощью корреляционного анализа можно установить наличие связи между двумя или более случайными величинами. Оценкой связи служит коэффициент корреляции при наличии линейной связи между величинами и нормальном законе их совместного распределения.

Дисперсионный анализ можно использовать для установления относительного влияния различных факторов на значения выходных характеристик. При этом общая дисперсия характеристики разлагается на компоненты, соответствующие рассматриваемым факторам. По значениям отдельных компонентов делают вывод о степени влияния того или другого фактора на анализируемую характеристику.

Когда все факторы в эксперименте являются количественными, можно найти аналитическую зависимость между характеристиками и факторами. Для этого используются методы регрессионного анализа.

К анализу результатов моделирования можно отнести задачу анализа чувствительности модели к вариациям ее параметров. Под анализом чувствительности понимают проверку устойчивости характеристик процесса функционирования системы к возможным отклонениям значений параметров.

Использование результатов моделирования

Результаты моделирования используются для принятия решения о работоспособности системы, для выбора лучшего проектного варианта или для оптимизации системы. Решение о работоспособности принимается по тому, выходят или не выходят характеристики системы за установленные границы при любых допустимых изменениях параметров. При выборе лучшего варианта из всех работоспособных вариантов выбирается тот, у которого максимальное значение критерия эффективности. Наиболее общей и сложной является оптимизация системы: требуется найти такие сочетания значений переменных параметров системы или рабочей нагрузки из множества допустимых, которое максимизирует значение критерия эффективности:

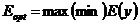
при соблюдении ограничений на все 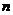 характеристик

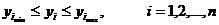
Если выходная характеристика 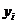 является случайной величиной с некоторой плотностью распределения 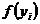, целесообразно ввести в задачу оптимизации стохастические ограничения следующего вида:
,
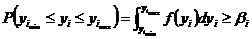где 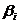 - минимально допустимая вероятность того, что конкретные значения  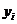не выйдут за ограничивающие пределы.