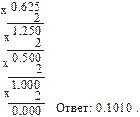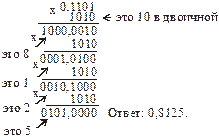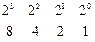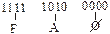Двоичная система счисления – это система, в которой используются только знаки 0 и 1. Исследования в этой системе начались в XIV веке. Основное достоинство – это удобство и простота. (Удобство реализации в машине: ток есть или нет, намагничен или нет участок и т.д.)
Рассмотрим, как реализуются четыре основные арифметические операции в такой системе.
Сложение. Используем следующую таблицу для сложения двоичных чисел Х и Y.
| X
| Y
| S
|  | Факт переноса 1 в более старший разряд
| |  0 0
|
|
|
| Пример: 5 + 11 = 16.
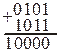
|
Вычитание. Используем таблицу для вычитания двоичных чисел X и Y.
| Факт заёма 1
из старшего разряда
| |  X X
| Y
| S
|  0 0
|
|
|
| Реально в машине вычитание заменяется сложением чисел согласно формуле: А–В=А+(–В).
Величина В представляется в дополнительном коде.
|
Умножение. Умножение реализуется с помощью двух операций: сложения и сдвига. Произведение получается суммированием частичных сумм и сдвигом. Сдвиг можно производить влево и вправо. Соответственно множитель анализируется, начиная с младшего или старшего разряда. Если в текущем разряде множителя 1, суммирование производит, если 0 – не производят.
| Иллюстрация умножения фактически выглядит также как и в десятичной системе. В примере умножение выполняется, начиная с младших разрядов множителя.
| 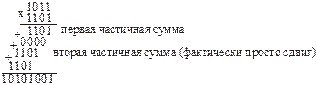
|
Деление. Деление основано на выделении из делимого минимальной группы разрядов, которая больше или равна делителю. Далее, выполняя правила деления, как в десятичной системе, можно получить результат.
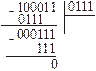
| Пример: 35:7=5
|
Методы перевода чисел из одной системы счисления в другую. Трудно ли изображать число в других системах счисления? Нисколько. Согласно (2) число отображается как
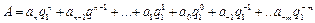 , (4)
, (4)
следовательно, достаточно определить новые коэффициенты b (вместо а) в системе с основанием q2 (вместо q1). Процесс получения новых коэффициентов заключается в последовательном делении числа на основание q2 х раз, пока частное не станет меньше делителя.
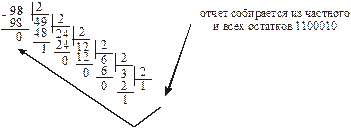
| Например, представить число 98 в десятичной системе счисления в двоичной системе.
|
Обратное преобразование заключается в последовательном выделении цифр в каждом разряде числа, умножении цифры на основание системы счисления q1 в степени, соответствующей разряду (нумерация с 0). Например, обратное преобразование:
1100010(2)=0·20+1·21+0·22+0·23+0·24+1·25+1·26=98(10).
Теперь, зная метод перевода, можно восстановить автобиографию как:
«Я окончил университет 24 лет отроду, спустя год 25-летним молодым человеком я познакомился с 19-летней девушкой. Незначительная разница в возрасте – всего 6 лет – способствовала тому, что мы жили душа в душу…»
Способы перевода дробей. Дробное число можно представить как
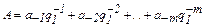 (5)
(5)
в новой системе оно будет как 0, в-1в-2…в-k. Т.е. требуется поочередное умножение данной дроби на другое основание системы счисления с выделением целой части.
Пример: Представить десятичную дробь 0,453 в 5-ричной системе счисления с точностью 5-4.
0,453=4·10-1+5·10-2+3·10-3
 0,453·5= 2,265
0,453·5= 2,265
0,265·5= 1,325
0,325·5= 1,625
0,625·5= 3,125
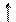 выбираем целые. Ответ 0,2113.
выбираем целые. Ответ 0,2113.
Проверка: 0,2113=2·5-1+1·5-2+1·5-3+3·5-4.
Пример: Представить десятичную дробь 0,625 в двоичной системе счисления.
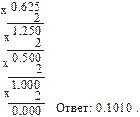
| Перевести дробь 0,1101 из двоичной системы счисления в десятичную.
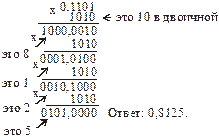
|
При переводе можно получить бесконечную дробь, поэтому процесс завершают, если достигнута заданная точность. При переводе чисел, у которых есть и целая, и дробная часть, требуется раздельный перевод.
Используя вышеописанные алгоритмы перевода дробных чисел в заданную систему счисления, рассмотрим пример с 16-ричной системой, допустим требуется число FA0 преобразовать в десятичную систему:
FA0=0·160+10·161+15·162=4000.
Для перевода из 16-ричной в двоичную специальных процедур не требуется, поскольку одна 16-ричная цифра соответствует четырем двоичным разрядам:
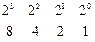
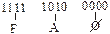
Аналогично просто преобразование между 8-ричной и двоичной системами, с той разницей, что вместо тетрады (4хразрядов) здесь используют триаду (3 разряда).


 0
0
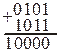
 X
X

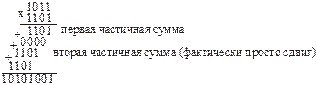
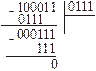
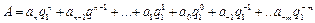 , (4)
, (4)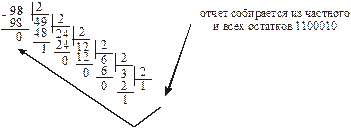
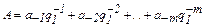 (5)
(5) 0,453·5= 2,265
0,453·5= 2,265 выбираем целые. Ответ 0,2113.
выбираем целые. Ответ 0,2113.