Арифметические действия над двоичными числами производятся по тем же правилам, что и над десятичными. Необходимо только учитывать, что сложение двух единиц дает нуль в данном разряде и единицу переноса в следующий.
Задача 2.8. Найти сумму двух чисел 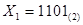 и
и 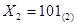 .
.
В дальнейшем, для упрощения записи, указанную задачу будем формулировать в следующем виде:
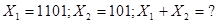
Решение: 1101
+ 101
Ответ: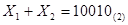
Сложение чисел с фиксированной запятой с различными знаками благодаря использованию обратного или дополнительного кода для отрицательных чисел сводится в ЭВМ к арифметическому сложению кодов чисел. Знаковые разряды участвуют в операции сложения наравне с цифровыми. При этом если выполняется операция сложения в обратных кодах, единица переноса из знакового разряда суммы прибавляется к её младшему разряду (т. е. выполняется циклический перенос). Если же операция сложения выполняется над числами, представленными в дополнительном коде, то единица переноса из знакового разряда суммы отбрасывается. Переход от обратного и дополнительного кодов к прямому выполняется аналогично переходу от прямого кода к обратному и дополнительному соответственно.
Рассмотрим некоторые правила сложения чисел в обратном и дополнительном кодах.
1. Результат сложения чисел, представленных в обратном коде, получится в обратном коде (если сумма отрицательна). Для перевода числа из обратного кода в прямой значения цифровых разрядов меняются на противоположные.
2. Для формирования правильного результата необходимо выполнить циклический перенос единицы. Если сумма положительна, то результат соответствует прямому коду суммы.
Сложение с использованием обратных кодов, как и в случае дополнительных кодов, выполняется по обычным правилам сложения двоичных чисел (при этом знаковый разряд рассматривается наравне с цифровыми), с той лишь разницей, что в случае обратных кодов в процессе получения суммы реализуется (при необходимости) циклический перенос, тогда как при дополнительных кодах единица переноса из знакового разряда не учитывается (отбрасывается). Следовательно, в общем виде реализация операции сложения в дополнительных кодах проще по сравнению с реализацией сложения в обратных кодах. Однако достигается это за счет усложнения операции кодирования чисел.
Следует также иметь в виду, что при сложении двух одинаковых по абсолютной величине чисел с разными знаками в случае использования обратных кодов получается отрицательный нуль (1,11... 11 либо 1.11...1). В ЭВМ отрицательный нуль автоматически преобразуется в положительный (т. е. к виду 0,00...0 при сложении правильных дробей либо 0.00...0 при сложении целых чисел соответственно). При сложении двух чисел с одинаковыми знаками возможно переполнение разрядной сетки сумматора (устройства, реализующего операцию сложения). Это, очевидно, приводит к существенному искажению результата.
Знак суммы (содержимое знакового разряда) может измениться по отношению к знаку слагаемых лишь в том случае, если при выполнении операции сложения имел место перенос либо только из знакового разряда суммы (при сложении отрицательных чисел), либо только в знаковый разряд (при сложении положительных чисел). При наличии переносов из знакового разряда и в знаковый разряд знак суммы совпадает со знаком слагаемых. Поэтому в ЭВМ для обнаружения факта переполнения разрядной сетки сумматора анализируются не знаки, а лишь факт наличия (отсутствия) переноса из знакового разряда и в знаковый разряд.
Следует иметь в виду, что при выполнении операции сложения в дополнительном коде возможна ситуация (единственная), когда указанное правило не различает переполнение. Это происходит тогда, когда сумма модулей двух отрицательных чисел равна удвоенному весу единицы старшего разряда числа (для правильной дроби — единице).
В некоторых ЭВМ для обнаружения переполнения применяют так называемые модифицированные коды (прямой, обратный и дополнительный), которые отличаются от основных (немодифицированных) лишь тем, что под поле знаков выделены два разряда. Например, число 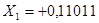 в прямом модифицированном коде имеет вид
в прямом модифицированном коде имеет вид
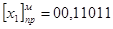 ; число
; число 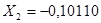 в обратном модифицированном коде записывается как
в обратном модифицированном коде записывается как 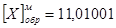 и пр.
и пр.
Сложение чисел в модифицированных кодах выполняется по тем же правилам, что и в основных кодах. Признаком переполнения здесь является различие содержимых знаковых разрядов: комбинация 01 фиксирует переполнение при сложении двух положительных чисел (положительное переполнение), а 10 — двух отрицательных (отрицательное переполнение). Заметим, что та же особая ситуация, возникающая при сложении отрицательных чисел в дополнительном коде, не различается и в модифицированном дополнительном коде. Если числа 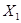 и
и 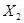 представлены в форме с плавающей запятой, т. е.
представлены в форме с плавающей запятой, т. е. 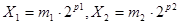 , то для их сложения необходимо
, то для их сложения необходимо 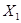 и
и 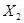 привести к общему порядку
привести к общему порядку 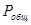 . Если, например,
. Если, например, 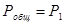 , то приведение к общему порядку отразится лишь на
, то приведение к общему порядку отразится лишь на 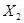 .
.
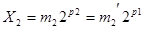
Далее можно общий множитель вынести за скобки и провести сложение мантисс:
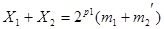
Очевидно, при конечной длине поля цифр мантиссы 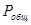 необходимо выбирать из условия
необходимо выбирать из условия 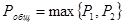 , так как в противном случае произойдет переполнение разрядной сетки мантиссы преобразуемого числа (в памяти машины числа с плавающей запятой хранятся в нормализованном виде).
, так как в противном случае произойдет переполнение разрядной сетки мантиссы преобразуемого числа (в памяти машины числа с плавающей запятой хранятся в нормализованном виде).
В ЭВМ определен следующий порядок выполнения операции сложения чисел, представленных в форме с плавающей запятой.
1. Вычитание порядков складываемых чисел. Если разность порядков равна нулю, порядки равны, то перейти к пункту 3. Если порядки не равны, то осуществить выравнивание порядков (пункт 2).
2. Увеличение меньшего из порядков до большего. Мантисса числа с меньшим порядком сдвигается вправо на число разрядов, равное разности порядков.
3. Сложение мантисс. Если не произошло переполнения разрядной сетки мантиссы и сумма получена в нормализованном виде, то вычисления закончить. Сумма мантисс является мантиссой суммы чисел, а порядок суммы чисел равен порядку большего числа (или общему порядку). В противном случае перейти к пункту 4.
4. Нормализация полученной суммы вправо (при переполнении разрядной сетки мантиссы) или влево (при наличии в мантиссе нулей). При нормализации вправо мантиссу суммы сдвинуть вправо на один разряд, а порядок суммы увеличить на единицу. При нормализации влево мантиссу суммы сдвинуть влево до первой значащей цифры, а порядок суммы уменьшить на такое же количество единиц.

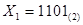 и
и 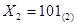 .
.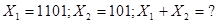
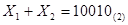
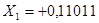 в прямом модифицированном коде имеет вид
в прямом модифицированном коде имеет вид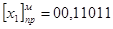 ; число
; число 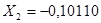 в обратном модифицированном коде записывается как
в обратном модифицированном коде записывается как 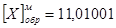 и пр.
и пр.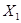 и
и 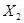 представлены в форме с плавающей запятой, т. е.
представлены в форме с плавающей запятой, т. е. 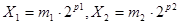 , то для их сложения необходимо
, то для их сложения необходимо 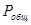 . Если, например,
. Если, например, 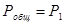 , то приведение к общему порядку отразится лишь на
, то приведение к общему порядку отразится лишь на 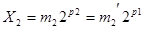
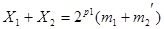
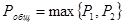 , так как в противном случае произойдет переполнение разрядной сетки мантиссы преобразуемого числа (в памяти машины числа с плавающей запятой хранятся в нормализованном виде).
, так как в противном случае произойдет переполнение разрядной сетки мантиссы преобразуемого числа (в памяти машины числа с плавающей запятой хранятся в нормализованном виде).