Система счисления — это совокупность цифровых знаков и правил их записи, применяемая для однозначной записи чисел. Все системы счисления подразделяются на позиционные и непозиционные.
Непозиционной называется такая система счисления, в которой значение цифры не зависит от ее положения в ряду цифр, изображающих число. Примером является римская система счисления, в которой для обозначения отдельных чисел используются буквы римского алфавита. Цифры в римской системе обозначаются различными знаками:
1 — I; 3 — III; 5 — V; 10 — X; 50 — L; 100 — С; 500 — D; 1000 — М. Запись числа осуществляется по каждый меньший знак, поставленный справа от прибавляется к его значению, а слева — вычитается из него: так, ХС — 90; СХ — 110; MCMLXXXVIII — 1988. Выполнять арифметические действия в непозиционных системах неудобно. Поэтому в настоящее время эти системы не используются для расчетов.
Позиционной называется такая система счисления, в которой значение цифры зависит от ее положения в ряду цифр, изображающих число, т. е. веса. В десятичной системе счисления вес каждой последующей цифры в 10 раз больше веса предыдущей. Например, цифра 2 в 1235 имеет значение 200, так как она в третьей справа позиции числа.
Позиционная система счисления (ПСС) характеризуется количеством различных цифр, используемых для записи чисел. Максимальное количество различных цифр, используемых для записи чисел в данной системе счисления, называется основанием системы счисления.
Любое число, записанное в р-ичной ПСС, может быть представлено в следующем виде:
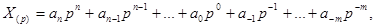 (2.1)
(2.1)
где 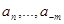 — любая цифра (символ), используемая в данной ПСС из множества {0,1,..., р — 1}; n, … , m — номера разрядов числа; р — основание ПСС, которым может быть любое целое число, кроме
— любая цифра (символ), используемая в данной ПСС из множества {0,1,..., р — 1}; n, … , m — номера разрядов числа; р — основание ПСС, которым может быть любое целое число, кроме 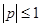 и
и 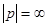 ;
; 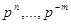 — веса разрядов. Например, число = 1235,87 по (2.1) имеет вид:
— веса разрядов. Например, число = 1235,87 по (2.1) имеет вид:
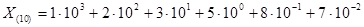
В ЭВМ применяют ПСС с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную и др.. В таблице показано соответствие записи чисел в десятичной, восьмеричной и шестнадцатеричной системах счисления.
Двоичная ПСС получила самое широкое применение в ЭВМ благодаря следующим достоинствам.
1. Числовая информация в ЭВМ отождествляется с состоянием используемых двоичных физических элементов. В двоичной ПСС 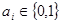 . Поэтому для физического представления
. Поэтому для физического представления 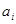 достаточно использования элементов с устойчивыми состояниями, кодируемыми 1 и 0. Например, транзистор может быть в открытом или закрытом состоянии, а следовательно, иметь на выходе высокое или низкое напряжение, ферритовый сердечник в устойчивом состоянии может иметь положительную или отрицательную остаточную магнитную индукцию, лампочка включена или выключена, отверстия на перфокарте пробиты или нет. Такие элементы принято называть двухпозиционными или двоичными. Очевидно, что реализация элементов, которые должны различать одно из двух состояний (0 или 1), оказывается проще и надежнее, чем реализация элементов, которые должны различать одно из 10 состояний.
достаточно использования элементов с устойчивыми состояниями, кодируемыми 1 и 0. Например, транзистор может быть в открытом или закрытом состоянии, а следовательно, иметь на выходе высокое или низкое напряжение, ферритовый сердечник в устойчивом состоянии может иметь положительную или отрицательную остаточную магнитную индукцию, лампочка включена или выключена, отверстия на перфокарте пробиты или нет. Такие элементы принято называть двухпозиционными или двоичными. Очевидно, что реализация элементов, которые должны различать одно из двух состояний (0 или 1), оказывается проще и надежнее, чем реализация элементов, которые должны различать одно из 10 состояний.
2. Арифметические операции выполняются наиболее просто. Например, таблицы сложения и умножения одноразрядных двоичных чисел имеют соответственно вид:
0 + 0 = 0; 0 * 0 = 0;
0 + 1 = 1; 0 * 1 = 0;
1 + 0 = 1; 1 * 0 = 0;
1 + 1 = 10; 1 * 1 = 1.
3. Процесс синтеза схем ЭВМ упрощен, так как обозначение переменных и функций в используемом математическом аппарате алгебры логики, принимающих два значения 0 или 1, совпадает с двоичными цифрами.
В то же время громоздкость записи чисел в двоичной ПСС и трудность их восприятия человеком (см. табл.) приводит к необходимости перевода исходных данных (чисел) из десятичной системы счисления в двоичную, а результатов — из двоичной в десятичную. Эти переводы осуществляются в ЭВМ автоматически по определенным программам.
В соответствии с формулой (2.1) числа в разных ПСС можно представить следующим образом:
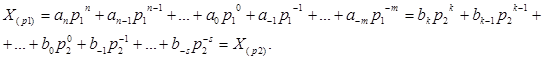 (2.2)
(2.2)
Следовательно, в общем виде задачу перевода числа из ПСС с основанием 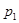 в ПСС с основанием
в ПСС с основанием 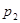 , формулируемую в виде:
, формулируемую в виде:
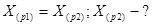 (2.3)
(2.3)
можно представить как задачу определения коэффициентов 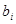 нового ряда, изображающего число в ПСС с основанием
нового ряда, изображающего число в ПСС с основанием 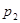 .
.
Решение (2.3) непосредственно в виде (2.2) осуществляют при «ручном» способе перевода чисел из одной ПСС в другую. Для «машинной» реализации перевода применяют следующие методы.

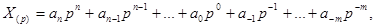 (2.1)
(2.1)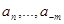 — любая цифра (символ), используемая в данной ПСС из множества {0,1,..., р — 1}; n, … , m — номера разрядов числа; р — основание ПСС, которым может быть любое целое число, кроме
— любая цифра (символ), используемая в данной ПСС из множества {0,1,..., р — 1}; n, … , m — номера разрядов числа; р — основание ПСС, которым может быть любое целое число, кроме 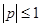 и
и 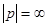 ;
; 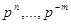 — веса разрядов. Например, число = 1235,87 по (2.1) имеет вид:
— веса разрядов. Например, число = 1235,87 по (2.1) имеет вид: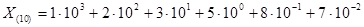
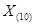
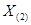
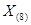
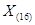
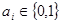 . Поэтому для физического представления
. Поэтому для физического представления 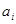 достаточно использования элементов с устойчивыми состояниями, кодируемыми 1 и 0. Например, транзистор может быть в открытом или закрытом состоянии, а следовательно, иметь на выходе высокое или низкое напряжение, ферритовый сердечник в устойчивом состоянии может иметь положительную или отрицательную остаточную магнитную индукцию, лампочка включена или выключена, отверстия на перфокарте пробиты или нет. Такие элементы принято называть двухпозиционными или двоичными. Очевидно, что реализация элементов, которые должны различать одно из двух состояний (0 или 1), оказывается проще и надежнее, чем реализация элементов, которые должны различать одно из 10 состояний.
достаточно использования элементов с устойчивыми состояниями, кодируемыми 1 и 0. Например, транзистор может быть в открытом или закрытом состоянии, а следовательно, иметь на выходе высокое или низкое напряжение, ферритовый сердечник в устойчивом состоянии может иметь положительную или отрицательную остаточную магнитную индукцию, лампочка включена или выключена, отверстия на перфокарте пробиты или нет. Такие элементы принято называть двухпозиционными или двоичными. Очевидно, что реализация элементов, которые должны различать одно из двух состояний (0 или 1), оказывается проще и надежнее, чем реализация элементов, которые должны различать одно из 10 состояний.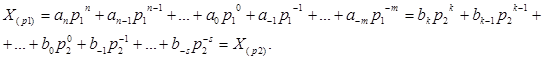 (2.2)
(2.2)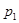 в ПСС с основанием
в ПСС с основанием 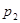 , формулируемую в виде:
, формулируемую в виде: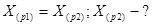 (2.3)
(2.3)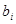 нового ряда, изображающего число в ПСС с основанием
нового ряда, изображающего число в ПСС с основанием