Пусть имеется двоичная нормализованная система с t разрядами. Пусть точное значение числа a представляет собой бесконечную двоичную дробь с экспоненциальным множителем:
.
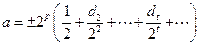Пусть приближенное значение получается в результате усечения – отбрасывания всех разрядов, начиная с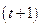 
-го:
, –
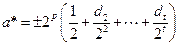тогда абсолютная ошибка равна
.
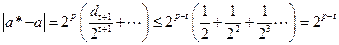В нормализованной системе
.
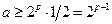Следовательно, относительная ошибка удовлетворяет неравенству:
.
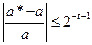Если вместо простого отбрасывания младших разрядов используется округление, то можно считать, что относительная ошибка в два раза меньше:
.
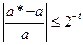Отсюда следует, что точное число и соответствующее ему округленное число связаны равенством:
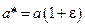, где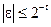 
.
Число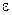 
называется машинный эпсилон. Машинный эпсилон характеризует точность арифметики с плавающей запятой.
Машинный эпсилон определяют как наименьшее число 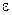, такое, что 
.
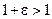Один из вариантов оценки числа на языке пакета Mathematica:
For[ ep=1.; s=2., s>1., ep=ep/2; s=ep+1. ]; 2 ep
Исходное число ep=1. делится многократно пополам до тех пор, пока не будет нарушено условие 
На печать выводится удвоенный результат последнего деления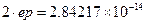 
.
Отметим, что в библиотеках языка Си имеются встроенные значения машинного эпсилон для формата float: FLT_EPSILON=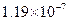
и для формата double: DBL_EPSILON=
.
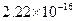