Содержание
1.1. Перевод чисел из одной системы счисления в другую.. 2
1.2. Представление чисел в системах с плавающей запятой. 2
1.3. Оценки погрешности. 3
1.4. Машинный эпсилон. 3
1.5. Погрешности вычисления значений функций. 4
1.6. Примеры неустойчивости алгоритмов. 5
1.7. Пример Уилкинсона. 5
1.1. Перевод чисел из одной системы счисления в другую
Перевод десятичной дроби в двоичную систему: последовательное сравнение дроби с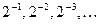 
. Для выполнения этого число 
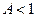умножим на 2 и сравним с 1: если 
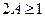, в старший разряд двоичной дроби запишем 1, иначе запишем 0. Обозначим дробную часть числа 
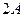буквой 
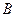. Теперь сравним с единицей число 
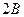и запишем в следующий разряд двоичной дроби 1 или 0. Продолжим подобным образом процесс заполнения двоичных разрядов, на каждом шаге умножая на 2 дробную часть числа, полученного на предыдущем шаге.
Пример 1.1. Найдем двоичное представление числа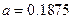 
. Выполняя описанный алгоритм, находим последовательность чисел:
.
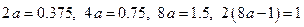Следовательно, двоичное представление числа имеет вид: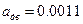 
.
Пример 1.2. Найдем двоичное представление числа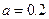 
. Последовательно находим:
.
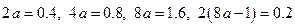Далее процесс повторяется. Получаем, что данное число в двоичной системе описывается бесконечной, периодической дробью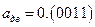 
. В скобках записан период дроби. Следовательно, при использовании двоичной дроби конечной длины возникает ошибка округления. Например, 
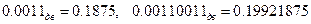. При большом количестве знаков ошибка округления мала, но она всегда присутствует.
