Вычисление конечных сумм и произведений - это наиболее часто встречающийся тип элементарных задач, шаблон решения которых должен быть заучен как 2*2. Какова бы не была сложность выражений, стоящих под знаком конечной суммы с заданным числом слагаемых, задачу всегда можно записать в виде:

| (1.2)
|
и применить для ее решения следующий шаблон:
S=0;for(int k=1; k<=n; k++){ //Вычислить текущий член суммы ak … S+=ak;} Часто приходится пользоваться слегка расширенным шаблоном:
Init;for(int k=1; k<=n; k++){ //Вычислить текущий член суммы ak … S+=ak;} В этом шаблоне Init представляет группу операторов, которые инициализируют используемые в цикле переменные значения, обеспечивающие корректность применения цикла. В частном случае, рассмотренном выше, инициализация сводится к заданию значения переменной S. Заметьте, если перед началом цикла не позаботиться о том, чтобы эта переменная была равна нулю, то после завершения цикла корректность результата не гарантируется.
В этой схеме основные проблемы могут быть связаны с вычислением текущего члена суммы ak. Нужно понимать, что ak - это не массив, а скаляр - простая переменная. Значения этой переменной вычисляются заново на каждом шаге цикла, задавая очередной член суммирования. Кроме того, следует заботиться об эффективности вычислений, применяя два основных правила, позволяющие уменьшить время вычислений.
Чистка цикла. Все вычисления, не зависящие от k, следует вынести из цикла (в раздел Init).
Рекуррентная формула. Часто можно уменьшить время вычислений ak, используя предыдущее значение ak, построив рекуррентную формулу  . Этот прием с успехом применяется как при вычислении функции
. Этот прием с успехом применяется как при вычислении функции  по формуле 1.1, так и при аналогичных вычислениях большинства других математических функций.
по формуле 1.1, так и при аналогичных вычислениях большинства других математических функций.
Покажем на примере формулы 1.1, как можно построить необходимые рекуррентные соотношения. Запишем соотношения для 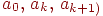 :
:
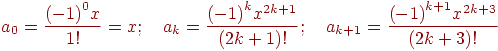
| (1.3)
|
Вычислив отношение  , получим требуемое рекуррентное соотношение:
, получим требуемое рекуррентное соотношение:
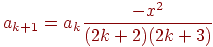
| (1.4)
|
Значение 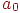 задает базис вычислений, позволяя инициализировать начальное значение переменной ak, а соотношение 1.4 позволяет каждый раз в теле цикла вычислять новое значение этой переменной. Заметьте: введение рекуррентного соотношения позволило избавиться от вычисления факториалов и возведения в степень на каждом шаге цикла.
задает базис вычислений, позволяя инициализировать начальное значение переменной ak, а соотношение 1.4 позволяет каждый раз в теле цикла вычислять новое значение этой переменной. Заметьте: введение рекуррентного соотношения позволило избавиться от вычисления факториалов и возведения в степень на каждом шаге цикла.
Иногда следует ввести несколько дополнительных переменных, хранящих вычисленные значения предыдущих членов суммы. Рекуррентная формула выражает новое значение ak через предыдущее значение и дополнительные переменные, если они требуются. Начальные значения ak и дополнительных переменных должны быть корректно установлены перед выполнением цикла в разделе Init. Заметьте, если начальное значение ak вычисляется в разделе Init до цикла, то схема слегка модифицируется - вначале выполняется прибавление ak к S, а затем новое значение ak вычисляется по рекуррентной формуле.
А теперь поговорим о том, как справляться с бесконечными суммами, примером которых является формула 1.1. Для математики бесконечность естественна. Множество целых чисел бесконечно, множество рациональных чисел бесконечно, множество вещественных чисел бесконечно. Элементы первых двух множеств можно пронумеровать - они задаются счетными множествами, множество вещественных чисел несчетно. Сколь угодно малый промежуток вещественной оси мы бы не взяли, там находится бесконечно много вещественных чисел. Число  и другие иррациональные числа задаются бесконечным числом цифр, не имеющим периода.
и другие иррациональные числа задаются бесконечным числом цифр, не имеющим периода.
Мир компьютеров - это конечный мир, хотя в нем и присутствует стремление к бесконечности. Множества, с которыми приходится оперировать в мире компьютера, всегда конечны. Тип целых чисел в языках программирования - int - всегда задает конечное множество целых из некоторого фиксированного диапазона. В библиотеке FCL это наглядно подтверждается самими именами целочисленных типов System.Int16, System.Int32, System.Int64. Типы вещественных чисел - double, float - задают конечные множества. Это достигается не только тем, что диапазон задания вещественных чисел ограничен, но и ограничением числа значащих цифр, задающих вещественное число. Поэтому для вещественных чисел компьютера всегда можно указать наборы таких двух чисел, между которыми нет никаких других чисел. Иррациональности компьютер не знает - число ? всегда задается конечным числом цифр.
Там, где в математике идет речь о пределах, бесконечных суммах, сходимости к бесконечности, в компьютерных вычислениях аналогичные задачи сводятся к вычислениям с заданной точностью - с точностью 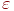 . Рассмотрим, например, задачу о вычислении предела числовой последовательности:
. Рассмотрим, например, задачу о вычислении предела числовой последовательности:
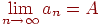
По определению число  является пределом числовой последовательности, если для любого сколь угодно малого числа
является пределом числовой последовательности, если для любого сколь угодно малого числа 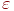 существует такой номер
существует такой номер  , зависящий от
, зависящий от 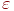 , что для всех
, что для всех  , больших
, больших  , числа
, числа  находятся в
находятся в 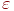 -окрестности числа
-окрестности числа  . Это определение дает основу для вычисления значения предела
. Это определение дает основу для вычисления значения предела  . Понятно, что получить точное значение
. Понятно, что получить точное значение  во многих случаях принципиально невозможно, - его можно вычислить лишь с некоторой точностью и тоже не сколь угодно малой, поскольку существует понятие "машинного нуля" - минимального числа, все значения меньше которого воспринимаются как нуль. Когда два соседних члена последовательности -
во многих случаях принципиально невозможно, - его можно вычислить лишь с некоторой точностью и тоже не сколь угодно малой, поскольку существует понятие "машинного нуля" - минимального числа, все значения меньше которого воспринимаются как нуль. Когда два соседних члена последовательности -  и
и 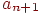 - начинают отличаться на величину по модулю меньшую чем
- начинают отличаться на величину по модулю меньшую чем  , то можно полагать, что оба члена последовательности попали в
, то можно полагать, что оба члена последовательности попали в 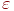 -окрестность числа
-окрестность числа  и
и 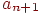 можно принять за приближенное значение числа
можно принять за приближенное значение числа  . Это рассуждение верно только при условии, что последовательность действительно имеет предел. В противном случае этот прием может привести к ошибочным выводам. Например, рассмотрим последовательность, элементы которой равны 1, если индекс элемента делится на 3, и равны 2, если индекс не делится на 3. Очевидно, что у этой последовательности предела нет, хотя существуют полностью совпадающие соседние члены последовательности.
. Это рассуждение верно только при условии, что последовательность действительно имеет предел. В противном случае этот прием может привести к ошибочным выводам. Например, рассмотрим последовательность, элементы которой равны 1, если индекс элемента делится на 3, и равны 2, если индекс не делится на 3. Очевидно, что у этой последовательности предела нет, хотя существуют полностью совпадающие соседние члены последовательности.
При вычислении на компьютере значения функции, заданной разложением в бесконечный сходящийся ряд, не ставится задача получения абсолютно точного результата. Достаточно вычислить значение функции с заданной точностью 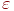 . На практике вычисления продолжаются до тех пор, пока текущий член суммы не станет по модулю меньше заданного
. На практике вычисления продолжаются до тех пор, пока текущий член суммы не станет по модулю меньше заданного 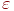 . Чтобы этот прием корректно работал, необходима сходимость ряда.
. Чтобы этот прием корректно работал, необходима сходимость ряда.
Вернемся к задаче вычисления функции  . Вот возможный шаблон решения:
. Вот возможный шаблон решения:
Init;while(Abs(ak) > EPS) { S+=ak; k++; //Вычислить новое значение ak … } При применении этого шаблона предполагается, что в разделе Init объявляются и должным образом инициализируются нужные переменные - S, ak, k. По завершению цикла переменная S содержит значение функции, вычисленное с заданной точностью.
Теперь мы готовы расширить определение класса, добавив код метода.


 . Этот прием с успехом применяется как при вычислении функции
. Этот прием с успехом применяется как при вычислении функции  по формуле 1.1, так и при аналогичных вычислениях большинства других математических функций.
по формуле 1.1, так и при аналогичных вычислениях большинства других математических функций.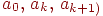 :
: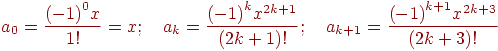
 , получим требуемое рекуррентное соотношение:
, получим требуемое рекуррентное соотношение: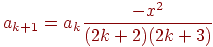
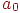 задает базис вычислений, позволяя инициализировать начальное значение переменной ak, а соотношение 1.4 позволяет каждый раз в теле цикла вычислять новое значение этой переменной. Заметьте: введение рекуррентного соотношения позволило избавиться от вычисления факториалов и возведения в степень на каждом шаге цикла.
задает базис вычислений, позволяя инициализировать начальное значение переменной ak, а соотношение 1.4 позволяет каждый раз в теле цикла вычислять новое значение этой переменной. Заметьте: введение рекуррентного соотношения позволило избавиться от вычисления факториалов и возведения в степень на каждом шаге цикла. и другие иррациональные числа задаются бесконечным числом цифр, не имеющим периода.
и другие иррациональные числа задаются бесконечным числом цифр, не имеющим периода.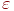 . Рассмотрим, например, задачу о вычислении предела числовой последовательности:
. Рассмотрим, например, задачу о вычислении предела числовой последовательности: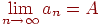
 является пределом числовой последовательности, если для любого сколь угодно малого числа
является пределом числовой последовательности, если для любого сколь угодно малого числа  , зависящий от
, зависящий от  , больших
, больших  находятся в
находятся в 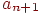 - начинают отличаться на величину по модулю меньшую чем
- начинают отличаться на величину по модулю меньшую чем  , то можно полагать, что оба члена последовательности попали в
, то можно полагать, что оба члена последовательности попали в