Пример 3.3. Быстрая сортировка массива
Написать программу, которая упорядочивает вещественный массив из 500 элементов методом быстрой сортировки.
Под сортировкой понимается упорядочивание элементов в соответствии с каким-либо критерием — чаще всего по возрастанию или убыванию. Существует множество методов сортировки, различающихся по поведению, быстродействию, требуемому объему памяти, а также ограничениям, накладываемым на исходные данные. Один из наиболее простых методов – сортировка выбором. Он характеризуется квадратичной зависимостью времени сортировки t от количества элементов N:
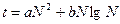 .
.
Здесь а и b — константы, зависящие от программной реализации алгоритма. Иными словами, для сортировки массив требуется просмотреть порядка N раз. Существуют алгоритмы и с лучшими характеристиками, например ‑ алгоритмом быстрой сортировки. Для него зависимость имеет вид
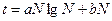 .
.
Рассмотрим этот алгоритм. Его идея состоит в следующем. К массиву применяется так называемая процедура разделения относительно среднего элемента. Вообще-то в качестве «среднего» можно взять любой элемент массива, но для наглядности будет выбираться элемент примерно из середины интервала.
Процедура разделения делит массив на две части. В левую помещаются элементы, меньшие элемента, выбранного в качестве среднего, а в правую ‑ большие. Это достигается путем просмотра массива попеременно с обоих концов, причем каждый элемент сравнивается с выбранным средним и элементы, находящиеся в «неподходящей» части, меняются местами. После завершения процедуры разделения средний элемент оказывается на своем окончательном месте, то есть его «судьба» определена, и мы можем про него забыть. Далее процедуру разделения необходимо повторить отдельно для левой и правой частей: в каждой части выбирается среднее, относительно которого она делится на две, и т. д.
Понятно, что одновременно процедура не может заниматься и левой, и правой частями, поэтому необходимо каким-то образом запомнить запрос на обработку одной из двух частей (например, правой) и заняться оставшейся частью (например, левой). Так продолжается до тех пор, пока не окажется, что очередная обрабатываемая часть содержит ровно один элемент. Тогда нужно вернуться к последнему из необработанных запросов, применить к нему все ту же процедуру разделения и т. д. В конце концов, массив будет полностью упорядочен.
Для хранения границ еще не упорядоченных частей массива более всего подходит структура данных, называемая стеком. Представьте себе длинный туннель, в который въезжает вереница машин. Ширина туннеля позволяет ехать только в один ряд. Если окажется, что выезд из туннеля закрыт и придется ехать обратно задним ходом, машина, ехавшая первой, сможет покинуть туннель в самую последнюю очередь. Это и есть стек, принцип организации которого — «первым пришел, последним ушел».
В приведенной далее программе, которую иллюстрирует рис. 3.4, стек реализуется в виде двух массивов stackl и stackr, а также переменной sp, используемой как «указатель» на вершину стека (она хранит номер последнего заполненного элемента массива).
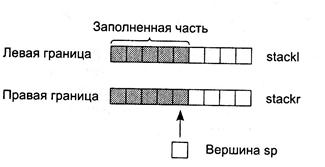
Рис. 3.4. Стек для хранения границ несортированных фрагментов массива
Для этого алгоритма количество элементов в стеке не может превышать п, поэтому размер массивов задан равным именно этой величине. При занесении в стек переменная sp увеличивается на единицу, а при выборке — уменьшается.
Ниже приведена программа, реализующая этот алгоритм:
program quicksort; const n = 500;
var
arr : array [1 .. n] of real;
middle : real; { средний элемент}
temp : real; { буферная переменная для обмена двух значений в массиве}
sp : integer; { указатель на вершину стека }
i, j : integer;
f : text;
stackl, stackr : array [1 .. n] of integer; { стеки границ фрагментов }
left, right : integer; {границы сортируемого фрагмента}
begin
assign(f, 'E:\input.txt'); reset(f);
for i := 1 to n do read(f, arr[i]);
sp := 1; stackl[1] := 1; stackr[1] := n; { 1 }
while sp > 0 do begin { 2 }
{ выборка границ фрагмента из стека: }
left := stackl[sp]; { 3 }
right := stackr[sp]; { 4 }
dec(sp); { 5 }
while left < right do begin { 6 }
{ разделение фрагмента arr[left] .. arr[right]: }
i := left; j := right; { 7 }
middle := arr[(left + right) div 2]; { 8 }
while i < j do begin { 9 }
while arr[i] < middle do inc(i); { 10 }
while middle < arr[j] do dec(j); { 11 }
if i <= j then begin
temp := arr[i]; arr[i] := arr[j]; arr[j] := temp; inc(i); dec(j);
end;
end;
if i < right then begin { 12 }
{ запись в стек границ правой части фрагмента: }
inc(sp);
stackl[sp] := i; stackr[sp] := right; end;
right := j; { 13 }
{ теперь left и right ограничивают левую часть }
end
end;
writeln(' Упорядоченный массив:');
for i := 1 to n do write(arr[i]:8:2);
writeln;
end.
На каждом шаге сортируется один фрагмент массива. Левая граница фрагмента хранится в переменной left, правая ‑ в переменной right. Сначала фрагмент устанавливается размером с массив целиком (оператор 1). В операторе 8 выбирается «средний» элемент фрагмента.
Для продвижения по массиву слева направо в цикле 10 используется переменная i, справа налево ‑ переменная j (в цикле 11). Их начальные значения устанавливаются в операторе 7. После того как оба счетчика «сойдутся» где-то в средней части массива, происходит выход из цикла 9 на оператор 12, в котором заносятся в стек границы правой части фрагмента. В операторе 13 устанавливаются новые границы левой части для сортировки на следующем шаге.
Если сортируемый фрагмент уже настолько мал, что сортировать его не требуется, происходит выход из цикла 6, после чего выполняется выборка из стека границ еще не отсортированного фрагмента (операторы 3 и 4). Если стек пуст, происходит выход из главного цикла 2. Массив отсортирован.
Итоги
1. Массив не является стандартным типом данных, он задается в разделе описания типов. Если тип массива используется только в одном месте программы, можно задать тип прямо при описании переменных.
2. Размерность массива может быть только константой или константным выражением. Рекомендуется задавать ее с помощью именованной константы.
3. Тип элементов массива может быть любым, кроме файлового, тип индексов — интервальным, перечисляемым или byte.
4. При описании массива можно задать начальные значения его элементов. При этом он описывается в разделе описания констант.
5. С массивами в целом можно выполнять только одну операцию — присваивание. При этом массивы должны быть одного типа. Все остальные действия выполняются с отдельными элементами массива.
6. Автоматический контроль выхода индекса за границы массива по умолчанию не выполняется. Можно включить его с помощью директивы {$R+}.
7. При работе с массивами удобно готовить исходные данные в текстовом файле и считывать их в программе.
Существует много алгоритмов сортировки. Они различаются по быстродействию, занимаемой памяти и области применения.
Организация ввода и вывода одномерного массива

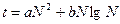 .
.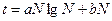 .
.