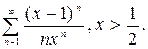Если телом цикла является циклическая структура, то такие циклы называют вложенными или сложными. Цикл, содержащий в себе другой цикл, называют внешним. Цикл, содержащийся в теле другого цикла, называют внутренним.
Внутренний и внешний циклы могут быть любыми из трех рассмотренных видов: циклами с параметром, циклами с предусловием, циклами с постусловием. При построении вложенных циклов необходимо соблюдать следующее дополнительное условие: все операторы внутреннего цикла должны полностью лежать в теле внешнего цикла, циклы ни в коем случае не могут пересекаться.
Сложные циклы условно разбивают на уровни вложенности. Ниже представлена структура вложенных циклов с параметром, для которой: внешний цикл 1 имеет уровень 0, внутренний цикл 2 – уровень 1, внутренний цикл 3 – уровень 2.
Возможная глубина вложенности циклов (количество уровней) ограничивается объемом имеющейся памяти ЭВМ. Заметим, что цикл 2 является внешним по отношению к циклу 3 и внутренним по отношению к циклу 1. Параметры циклов разных уровней изменяются не одновременно. Вначале все свои значения изменит параметр самого внутреннего цикла при фиксированных значениях параметров циклов с меньшим уровнем – это цикл 3. Затем меняется на один шаг значение параметра следующего уровня (цикла 2) и снова полностью выполняется внутренний цикл и т. д. до тех пор, пока параметры циклов всех уровней не примут все требуемые значения. При этом, если в сложном цикле с глубиной вложенности k число повторений циклов на каждом уровне равно N0, N1, …, Nk соответственно, то общее количество повторений тела самого внутреннего цикла равно: N= N0 × N1 × …× Nk.
Рисунок 7.12 – Схема алгоритма с вложенными циклами
На рисунке 7.12 изображен цикл с параметром. Но все изложенное относится и к тем случаям, когда для организации циклов используются другие виды циклических структур: цикл с предусловием или цикл с постусловием.
Рассмотрим конкретную задачу, требующую для своего решения организации вложенных циклов. Такой задачей является задача табулирования функции нескольких переменных.
Пример 5. Построить алгоритм и написать программу вычисления значений функцииz=cos x + y, гдеx = xn (hx) xk иy = yn (hy) yk . Аргументы функции x, y – действительные числа.
Для определения значений функции z для всех различных пар (x,y) необходимо процесс вычислений организовать следующим образом. Вначале при фиксированном значении одного из аргументов, например при x=x0, вычислить значения z для всех заданных y: yn , yn + hy , …, yn . Затем, изменив значение х на x + hx , вновь перейти к полному циклу изменения переменной y. Данные действия повторить для всех заданных x: xn , xn + hx , …, xn. При реализации данного алгоритма требуется структура вложенных циклов: внешнего цикла – для изменения значений переменной х и внутреннего цикла – для изменения значений переменной у. Причем в данной задаче внешний и внутренний циклы можно поменять местами, при этом изменится только очередность изменения аргументов при вычислении функции. В качестве внешнего и внутреннего циклов можно использовать циклы с параметром, циклы с предусловием или с постусловием.
Алгоритм решения поставленной задачи, выполненный с применением цикла с параметром, представлен на рисунке 7.13. Программа, соответствующая этому алгоритму, представлена в листинге 9.
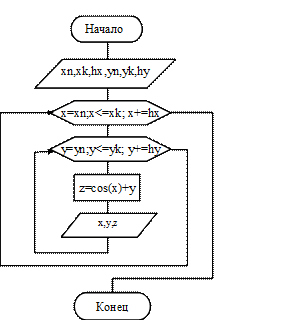
Рисунок 7.13 – Схема алгоритма к примеру 5
Листинг 9 – К примеру 5
using System;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
double xn, xk, hx, yn, yk, hy, z;
Console.Write("Enter xn ");
xn = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter xk ");
xk = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter hx ");
hx = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter yn ");
yn = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter yk ");
yk = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter hy ");
hy = Convert.ToDouble(Console.ReadLine());
for (double x = xn; x <= xk; x += hx) // Внешний цикл
{
for (double y = yn; y <= yk; y += hy) // Внутрений цикл
{
z = Math.Cos(x) + y;
Console.WriteLine("х=" + x + " у=" + y + " z=" + z);
}
}
}
}
}
Пример 6. Вычислить с погрешностью e значения функции y = cos(x), используя разложение cos x в ряд, для значений x = xn (hx) xk .
Вычислить значение функции cos x можно путем разложения его в следующий ряд:
Cos x = 1 - 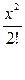 +
+ 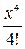 -
- 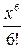 + …+(-1)n
+ …+(-1)n 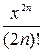 +...
+...
Задача вычисления y = cos x для фиксированного значения х была рассмотрена в примере 1. В данном случае сумму ряда S необходимо вычислять для каждого значения х из диапазона [xn , xk]. Следовательно, необходимо использовать структуру вложенных циклов.
Как показано на схеме алгоритма (рис. 7.14), внешний цикл – цикл для изменения значений переменной х (цикл с предусловием). Внутренний цикл – цикл для вычисления суммы ряда при фиксированном значении х с погрешностью вычислений e (также цикл с предусловием). Все вышесказанное реализовано в программе, соответствующей схеме данного алгоритма.
В данном случае сумму ряда Sнеобходимо вычислять для каждого значенияхиз диапазона [xn, xk]. Следовательно, необходимо использовать структуру вложенных циклов. Как показано на схеме алгоритма, внешний цикл – цикл для изменения значений переменной х (цикл с предусловием). Внутренний цикл – цикл для вычисления суммы ряда при фиксированном значениихс погрешностью вычислений e (также цикл с предусловием).
Правильность работы программы оценивается путем сравнения значения s с его вычисляемым по формуле y=cos(x) значением.
Соответствующая программа представлена в листинге 10.
Листинг 10
using System;
namespace ConsoleApplication1
{ class Program
{ static void Main(string[] args)
{ double xn, xk, hx, eps,s,t,y,f;
Console.Write("Enter xn ");
xn = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter xk ");
xk = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter hx ");
hx = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter eps ");
eps = Convert.ToDouble(Console.ReadLine());
double x= xn;
while (x<=xk)
{ s=0; //Внешний цикл
t=1;
int n=1;
while (Math.Abs(t) > eps)
{ s= s + t; //Внутренний цикл
f= -x*x / (2*n*(2*n-1));
t= t*f;
n++;
} //Конец внутреннего цикла
y= Math.Cos (x);
Console.WriteLine("х=" + x + " у=" + y+ " s="+s);
x= x + hx;
} //Конец внешнего цикла
}
}
}
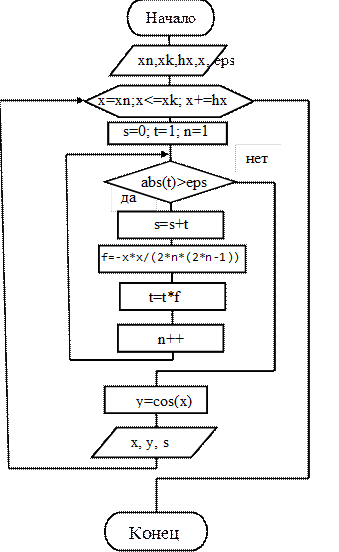
Рисунок 7.14 – Схема алгоритма к примеру 6
Выше были рассмотрены основные управляющие конструкции языка С#, позволяющие осуществлять программную реализацию различных ветвлений и циклов. Любой алгоритм (программа) представляет собой некоторую комбинацию рассмотренных стандартных структур: линейной, разветвляющейся, циклической.
Пример 7. Составить программу нахождения наибольшего общего делителя (НОД) двух целых чисел M и N.
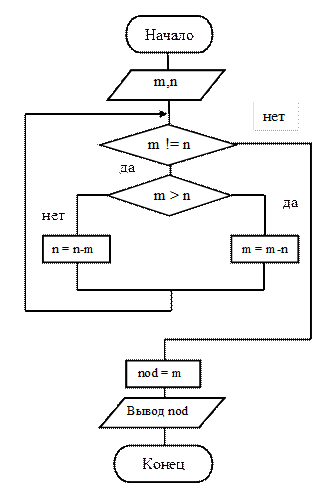
Рисунок 7.15 – Схема алгоритма к примеру 7
Программа представлена в листинге 11, схема алгоритма на рисунке 7.15.
Листинг 11
using System;
namespace ConsoleApplication1
{ class Program
{ static void Main(string[] args)
{ int m,n,nod;
Console.Write("Enter m ");
m = Convert.ToInt32(Console.ReadLine());
Console.Write("Enter n ");
n = Convert.ToInt32(Console.ReadLine());
while (m!=n)
{ if (m > n) m= m - n;
else n= n-m;
}
nod= m;
Console.WriteLine("nod=" + nod);
}
}
}
Программа представляет собой сочетание линейной, циклической и разветвляющейся структур. Телом цикла с предусловием является разветвление.
Пример 8. Составить программу табулирования сложной функции
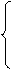 (a sin x+b cos x)[x]!, если x£ k;
(a sin x+b cos x)[x]!, если x£ k;
y = f(x) = 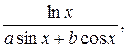 если x> k,
если x> k,
действительной переменной x = xn (hx) xk. Для вычисления ln x необходимо воспользоваться формулой:
ln x = 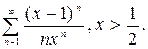
Вычисления произвести с погрешностью e.
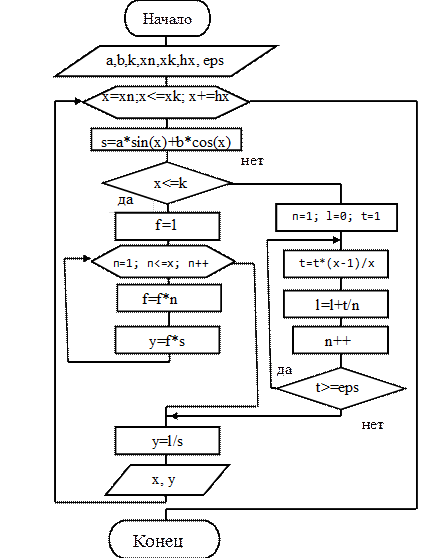
Рисунок 7.16 – Схема алгоритма к примеру 8
Алгоритм решения поставленной задачи представлен ниже (рис. 7.16).
Так как вычисление ln x должно производиться при х> 1/2, то при вводе данных необходимо предупредить пользователя о том, чтобы он обратил внимание на значение левой границы интервала изменения х, что и осуществляется в программе.
На первом этапе построим укрупненную схему с выделением операций ввода исходных данных и внешнего цикла по х. В программе этот цикл реализуем с помощью оператора цикла с параметром.
На втором этапе более детально раскроем тело цикла по х без расшифровки вычислений функций факториала и логарифма. Тело цикла представляет собой разветвляющуюся структуру. На последнем этапе раскроем внутренние циклы для вычисления функции ln x и x!
Для вычисления x! используем структуру цикла с параметром, так как x!=1×2…x.
Вычисление ln x осуществим накоплением суммы членов заданного ряда с требуемой точностью. Везде, где возможно, постараемся использовать рекуррентные формулы.
Программа, соответствующая этому алгоритму, представлена в листинге 12.
Листинг 12
using System;
namespace ConsoleApplication1
{ class Program
{ static void Main(string[] args)
{ double xn, xk, hx, eps, a, b, k, l, t, s, y = 0;
int f;
Console.Write("Enter a ");
a = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter b ");
b = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter k ");
k = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter eps ");
eps = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter xn >1/2 ");
xn = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter xk ");
xk = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter hx ");
hx = Convert.ToDouble(Console.ReadLine());
Console.WriteLine("Исходные данные");
Console.WriteLine("xn=" + xn + " xk=" + xk + " hx=" + hx);
Console.WriteLine("a=" + a + " b=" + b + " k=" + k + " eps=" + eps);
for (double x = xn; x <= xk; x += hx)
{s = a * Math.Sin(x) + b * Math.Cos(x);// Начало внешнего цикла
if (x <= k)
{ f = 1; // Вычисление факториала
for (int n = 1; n <= x; n++)
{ f = f * n;
y = f * s;
}
}
else
{ int n = 1; l = 0; t = 1; //Вычисление логарифма
do
{ t = t * (x - 1) / x;
l = l + t / n;
n++;
}
while (t >= eps);
y = l / s;
}
Console.WriteLine("x=" + x + " y=" + y);
} //Конец внешнего цикла
}
}
}
Пример 9. Дано целое число N. Написать программу для получения в порядке убывания всех делителей данного числа. В программе обеспечить пользовательский интерфейс, позволяющий вводить исходные данные и просматривать их, а также неоднократно производить вычисления, не выходя из программы. Для выхода из программы предусмотреть специальную команду.
Ниже приведена программа для решения данной задачи (лист. 13).
В данной программе для реализации поставленной задачи используется цикл с постусловием. С его помощью организуется возможность решения задачи с изменением исходных данных без выхода из программы и повторного ее запуска. Через пользовательское меню возможно осуществить повторный ввод и просмотр данных, получить результаты решения задачи.
Работа пользовательского интерфейса программы обеспечивается с помощью оператора множественного выбора. В данной программе значение селектора b вводится с клавиатуры пользователем. Далее это значение переменной b используется в операторе множественного выбора. Таким образом, пользователь, задавая это значение, определяет, какие операции будет выполнять компьютер. Так, если b=1, то программа выводит на экран предложение ввести исходные данные и считывает их. Если b=2, то на экран выводятся последние значения исходных данных, введенные пользователем. Если b=3, то осуществляется собственно решение задачи, и на экран выводится результат. И если b=4, то осуществляется выход из программы.
Листинг 13
using System;
namespace ConsoleApplication1
{ class Program
{ static void Main(string[] args)
{ int n=0,b;
do
{Console.WriteLine("- Нажмите 1 и Enter для ввода числа n ");
Console.WriteLine("- Нажмите 2 и Enter для просмотра исходных данных");
Console.WriteLine("- Нажмите 3 и Enter для выполнения программы");
Console.WriteLine("- Нажмите 4 и Enter для выхода из программы");
b = Convert.ToInt32(Console.ReadLine());
switch (b)
{ case 1: Console.WriteLine("ВВедите число n ");
n = Convert.ToInt32(Console.ReadLine()); break;
case 2: Console.WriteLine("n= " +n); break;
case 3: for (int i = n; i>= 1; i--)
{ if (n % i ==0) Console.WriteLine(i);
}
break;
}
}
while (b<4);
}
}
}

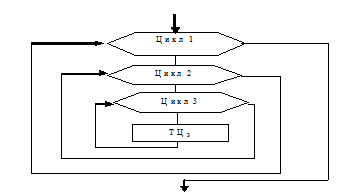

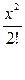 +
+ 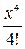 -
- 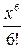 + …+(-1)n
+ …+(-1)n 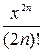 +...
+...

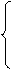 (a sin x+b cos x)[x]!, если x£ k;
(a sin x+b cos x)[x]!, если x£ k;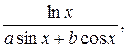 если x> k,
если x> k,