Интерполяционный поиск

Лине́йная интерполя́ция — интерполяция алгебраическим двучленом P₁(x) = ax + b функции f, заданной в двух точках x₀ и x₁ отрезка [a, b].

Геометрически это означает замену графика функции f прямой, проходящей через точки (x₀,f(x₀)) и (x₁,f(x₁)).

Уравнение такой прямой имеет вид:

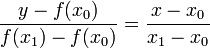
отсюда для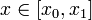

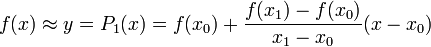
Это и есть формула линейной интерполяции

Отличие интерполяционного поиска от предыдущих методов

заключается в том, что выбор очередного ключа Ki для сравнения с аргу-

ментом А зависит не только от Q и P, но и от значений ключей KQ и Kp в

нижней и верхней границах интервала поиска. Если аргумент поиска А на

очередном шаге лежит между KQ и KP, то ключ Ki выбирается на расстоянии

(P-Q)(A-KQ)/(KP-KQ) от Q.

Алгоритм интерполяционного поиска также аналогичен алгоритму би-

нарного поиска. Отличие состоит только в шаге вычисления номе-

ра I сравниваемого элемента, который в данном случае имеет вид:

I = |_ (P-Q)(A-KQ)/(KP-KQ) _| + Q.

Пример. Осуществить интерполяционный поиск аргумента 51 в массиве

ключей: 20 25 29 32 37 38 39 51 53 57 61 99.

Q=1,KQ=20,P=12,KP=99,i=5,Ki=37: [20 25 29 32

Q=6,KQ=38,P=12,KP=99,i=8,Ki=51: 20 25 29 32 37[38 39

Поиск закончен удачно.