Динамическое программирование в— метод нахождения оптимальных решений сложных задач путём разбиения их на более простые подзадачи.
К задачам ДП относятся задачи перспективного и текущего планирования во времени, задачи многошагового нахождения оптимума при размещение производственных сил, задачи оптимального быстродействия и т.д.
Выделим задачи ДП:
1)
Он применим к задачам с оптимальной подструктурой (англ.), выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной. В этом случае время вычислений, по сравнению с «наивными» методами, можно значительно сократить.
Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.
Метод динамического программирования сверху — это простое запоминание результатов решения тех подзадач, которые могут повторно встретиться в дальнейшем. Динамическое программирование снизу включает в себя переформулирование сложной задачи в виде рекурсивной последовательности более простых подзадач.
Пусть дона некоторая физическая система S, находящаяся в некотором начальном состоянии 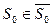 и являющаяся управляемой. Таким образом при осуществлении некоторого управления
и являющаяся управляемой. Таким образом при осуществлении некоторого управления 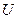 система переходит из состояния
система переходит из состояния 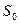 в конечное состояние
в конечное состояние 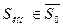 . При этом качество каждого из реализуемых управление
. При этом качество каждого из реализуемых управление 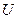 характеризуется соответствующим значением некоторой функции
характеризуется соответствующим значением некоторой функции 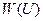 .
.
Задача состоит в том, чтобы из множества возможных управлений 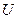 найти такое
найти такое 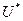 , чтобы функция
, чтобы функция 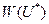 принимала свое максимальное или минимальное значение. Данная задача является общей задачей динамического программирования.
принимала свое максимальное или минимальное значение. Данная задача является общей задачей динамического программирования.
Пусть состояние системы характеризуется некоторой точкой S на плоскости 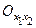
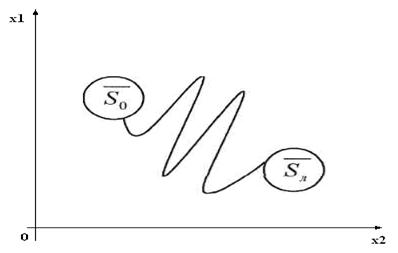
Данная точка благодаря некоторому управлению перемещается по линии изображения рисунка, из множества возможных начальных линий 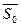 в область конечных состояний Каждому управлению
в область конечных состояний Каждому управлению 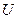 движением точки находится в соответствии некоторая функция
движением точки находится в соответствии некоторая функция 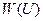 (длина пройденного пути под воздействием самого управления). Тогда задача состоит в том, чтобы из всех допустимых траекторий точки найти такую, которая получается в результате реализации управления U*. Обеспечивающего экстремальные значения функции
(длина пройденного пути под воздействием самого управления). Тогда задача состоит в том, чтобы из всех допустимых траекторий точки найти такую, которая получается в результате реализации управления U*. Обеспечивающего экстремальные значения функции 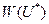 .
.
К определению такой траектории сводится задача динамического программирования, в случае когда допустимые состоянии системы S определяется точками двухмерного пространства (в общем случае 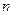 - мерного пространства).
- мерного пространства).
Интерпретация задач динамического программирования
Пример:
В распоряжении организации в подчинении у которой находится А предприятий, находятся средства в размере К тысяч у.е. Для использования их на развитие предприятий в течении 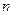 лет. Эти средства в начале каждого хозяйственного года, т.е. в моменты
лет. Эти средства в начале каждого хозяйственного года, т.е. в моменты 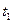 ,
,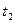 ,...,
,...,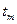 распределяются между предприятиями. Одновременно с этим между предприятиями распределяется полученная или за прошлый год прибыль. Таким образом в начале каждого
распределяются между предприятиями. Одновременно с этим между предприятиями распределяется полученная или за прошлый год прибыль. Таким образом в начале каждого 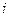 -года рассматриваемого периода
-года рассматриваемого периода 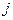 предприятие получает в свое распоряжение
предприятие получает в свое распоряжение 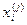 тысяч у.е.
тысяч у.е.
Задача состоит в определении таких значений, т.е. нахождение такого распределения выделения средств межу предприятиями и получаемой ими прибыли при которых за 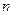 -лет обеспечивается премия максимальной прибыли всеми предприятиями.
-лет обеспечивается премия максимальной прибыли всеми предприятиями.
Формулировка данной задачи в терминах области динамического программирования.
Решение:
Пусть 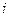 -oe предприятия на год
-oe предприятия на год 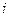 полученных тысяч рублей. Данное распределение средств пусти рассматриваются как реализация некоторого уравнения
полученных тысяч рублей. Данное распределение средств пусти рассматриваются как реализация некоторого уравнения 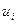 . Таким образом
. Таким образом 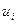 состоит в том, что на
состоит в том, что на 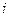 -м шаге первому предприятию выделяется
-м шаге первому предприятию выделяется 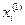 , второму -
, второму - 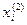 ,...,
,..., 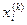 .
.
Совокупность этих чисел 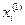 ,…,
,…,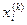 определяется совокупность управлений
определяется совокупность управлений 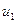 ,
, 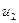 ,…,
,…,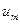 на
на 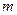 -шагов распределения средств как
-шагов распределения средств как 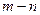 - мерного пространства.
- мерного пространства.
В качестве критерия оценки выбранного решения средств взята суммарная прибыль за 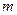 - лет, которое зависит от всей совокупности управлений
- лет, которое зависит от всей совокупности управлений 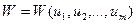
Нахождение решений задачи динамического программирования
Пусть рассматривается система S, состояние которой на 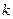 -ом шаге определяется совокупность чисел
-ом шаге определяется совокупность чисел 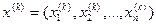 , полученных в результате управления
, полученных в результате управления 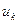 . Данные управления обеспечивают переход системы из состояния
. Данные управления обеспечивают переход системы из состояния 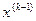 в
в 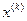 . При этом считается , что состояние
. При этом считается , что состояние 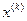 зависит только от управления
зависит только от управления 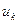 и предыдущего состояния, т.е.
и предыдущего состояния, т.е. 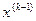 . Пусть в результате выполнения шага к обеспечивается некоторый переход или выигрыш, так же зависящий от состояния
. Пусть в результате выполнения шага к обеспечивается некоторый переход или выигрыш, так же зависящий от состояния 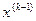 и управления
и управления 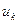 и равный соответственно
и равный соответственно 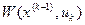 тогда общий доход или выигрыш за
тогда общий доход или выигрыш за 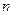 шагов будет записываться следующим образом.
шагов будет записываться следующим образом.
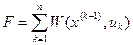
Принцип оптимальности:
Какого бы ни было состояния системы перед очередным шагом надо выбрать управление на этом шаге так, чтобы выигрыш на первом шаге + выигрыш на всех предыдущих шагах были максимальными.
Управление 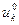 , выбранное при определенных добавлениях и предположениях о том, как значение предыдущий шаг называется условно оптимальным управлением.
, выбранное при определенных добавлениях и предположениях о том, как значение предыдущий шаг называется условно оптимальным управлением.
Математическая формулировка принципа оптимальности:
Пусть 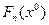 — это максимальный доход, полученный за
— это максимальный доход, полученный за 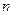 —шагов при переходе системы
—шагов при переходе системы 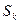 из начального состояния
из начального состояния 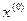 в конечное состояние
в конечное состояние 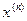 .
.
При условии оптимального управления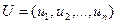 . Пусть
. Пусть 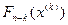 — это максимальный доход, получаемый при переходе системы из состояния
— это максимальный доход, получаемый при переходе системы из состояния 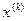 в конечное состояние
в конечное состояние 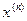 при оптимальной стратегии, состоящий из
при оптимальной стратегии, состоящий из 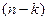 шагов. Тогда можно записать след:
шагов. Тогда можно записать след:
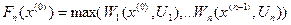
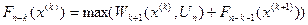 ,
, 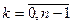
Последнее функциональное уравнение называется уравнением Беллимана. Используется данное уравнение находится решение задачи динамического программирования.
Оптимальное решение задачи методом динамического программирования находится на основе уравнения (6.1). Чтобы определить его, необходимо:
1) записать уравнения для последнего состояния процесса (ему соответствует 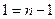 ):
):
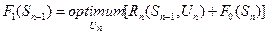
2) найти 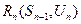 из дискретного набора его значений при некоторых фиксированных
из дискретного набора его значений при некоторых фиксированных 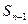 и
и 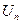 из соответствующих допустимых областей (так как
из соответствующих допустимых областей (так как 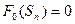 , то
, то 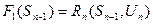 . В результате после первого шага известно решение
. В результате после первого шага известно решение 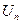 и соответствующее значение функции
и соответствующее значение функции 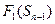 ;
;
3) уменьшить значение 1 на единицу и записать соответствующее функциональное уравнение. При 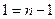 (
(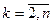 ) оно имеет вид
) оно имеет вид
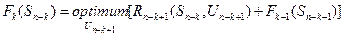 ; (6.2)
; (6.2)
4) найти условно-оптимальное решение на основе выражения (6.2);
5) проверить чему равно значение 1. Если 1=0, расчет условно-оптимальных решений закончен, при этом найдено оптимальное решение задачи для первого состояния процесса. Если 1<>0, перейти к выполнению пункта 3);
6) вычислить оптимальное решение задачи для каждого последующего шага процесса, двигаясь от конца расчетов к началу.
Пример Требуется перевезти груз из города А в город В. Сеть дорог, связывающих эти города, изображена на рис 6.1. Стоимость перевозки груза из города s(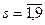 ) в город
) в город 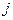 (
(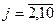 ) проставлена над соответствующими дугами сети. Необходимо найти маршрут , связывающий города А и В, для которого суммарные затраты на перевозку груза были бы наименьшими. На рис. 6.1. городам поставлены в соответствие вершины сети, обозначенные кружками с номером, а транспортным магистралям — дуги (линии со стрелками), соединяющие вершины.
) проставлена над соответствующими дугами сети. Необходимо найти маршрут , связывающий города А и В, для которого суммарные затраты на перевозку груза были бы наименьшими. На рис. 6.1. городам поставлены в соответствие вершины сети, обозначенные кружками с номером, а транспортным магистралям — дуги (линии со стрелками), соединяющие вершины.
Разобьем все множество вершин (городов) на подмножества. В первое подмножество включим исходную вершину 1. Во второе - вершины, в которые входят дуги, выходящие из вершины 1. В третье - вершины, в которые входят дуги, выходящие из вершин второго подмножества. Таким образом, продолжая разбиение дальше, получим пять подмножеств: {1},{2,3,4},{5,6,7},{8,9},{10}. Очевидно, что любой маршрут из города 1 в город 10 содержит ровно четыре дуги, каждая из которых связывает вершины, принадлежащие соответствующим подмножествам. Следовательно, процесс решения задачи (нахождения оптимального маршрута) разбивается на четыре этапа. На первом этапе принимается решение, через какой город, принадлежащий второму подмножеству, везти груз из города 1. На втором этапе необходимо определить, через какой город третьего подмножества везти груз из некоторого города, принадлежащего второму подмножеству и т.д.
Перенумеруем этапы от конечной вершины сети к начальной (рис.6.1) и введем обозначения: 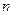 -номер шага(
-номер шага(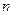 =1,2,3.4);
=1,2,3.4); 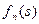 - минимальные затраты на перевозку груза от города s до конечного города, если до конечного города осталось
- минимальные затраты на перевозку груза от города s до конечного города, если до конечного города осталось 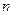 шагов;
шагов; 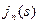 - номер города , через который нужно ехать из города s, чтобы досчитать
- номер города , через который нужно ехать из города s, чтобы досчитать 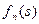 ;
; 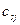 - - стоимость перевозки груза из города s в город
- - стоимость перевозки груза из города s в город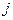 .
.
Здесь все обозначения несут важную смысловую нагрузку: 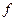 означает целевую функцию,
означает целевую функцию, 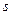 - состояние системы (номер города), индекс
- состояние системы (номер города), индекс 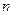 несет динамическую информацию о том, что из города s до конечного города осталось
несет динамическую информацию о том, что из города s до конечного города осталось 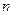 шагов.
шагов.
Предположим, что груз доставлен в город 10, следовательно, число оставшихся шагов равно нулю(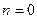 ) и
) и 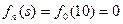 , так как из города s до конечного города осталось
, так как из города s до конечного города осталось 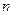 шагов.
шагов.
Рассмотрим, последний шаг (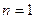 ) и вычислим для него значение функции. Очевидно, что в город 10 груз может быть доставлен или из города 8 ,или из города 9. Вычислим затраты на перевозку для этих двух состояний:
) и вычислим для него значение функции. Очевидно, что в город 10 груз может быть доставлен или из города 8 ,или из города 9. Вычислим затраты на перевозку для этих двух состояний:
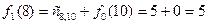 ,
, 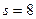 ,
, 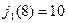 ;
;
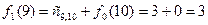 ,
, 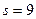 ,
, 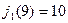 ;
;
Чтобы произвести расчет для 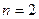 , выдвинем гипотезы о месте нахождения груза:
, выдвинем гипотезы о месте нахождения груза:
1-я гипотеза - груз находится в городе 5; 2-я гипотеза - груз находится в городе 6; 3-я гипотеза - груз находится в городе 7;
Из города 5 в город 10 можно провезти груз или через город 8, или через город 9. Поэтому оптимальный маршрут из города 5 найдется из выражения
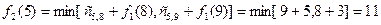
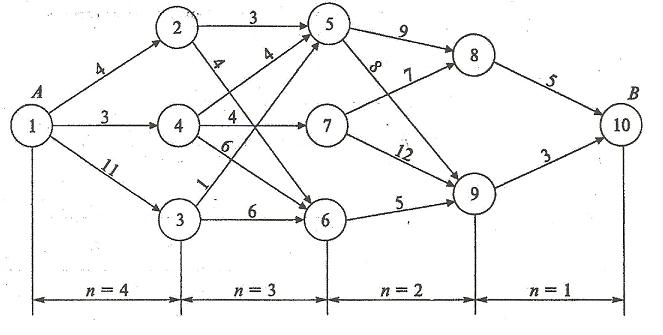
Рис. 6.1
Здесь 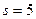 и
и 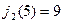 , т.е. условно-оптимальный маршрут проходит через город 9.
, т.е. условно-оптимальный маршрут проходит через город 9.
Аналогично находим значения функции для 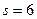 и
и 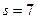 .
.
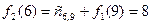
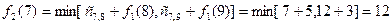
Все вычисления удобно выполнять в таблицах. Расчеты первого [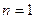 ,
, 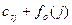 ] и второго [
] и второго [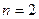 ,
, 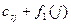 ] этапов помещены в табл.6.4 и 6.5 соответственно.
] этапов помещены в табл.6.4 и 6.5 соответственно.
таблица 6.4
таблица 6.5
Цифры в столбцах таблиц, находящиеся слева от жирной вертикальной черты, представляют собой сумму стоимости 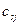 доставки груза из города s в город j и стоимости
доставки груза из города s в город j и стоимости 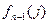 доставки груза от города
доставки груза от города 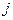 до города В. В каждой строке выбирается наименьшая из этих сумм. Этим определяется условно-оптимальные затраты на доставку груза из города s в конечный город. Затраты обозначены
до города В. В каждой строке выбирается наименьшая из этих сумм. Этим определяется условно-оптимальные затраты на доставку груза из города s в конечный город. Затраты обозначены 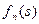 и записаны в первом столбце справа от вертикальной черты, а город, через который проходит условно-оптимальный маршрут, обозначен
и записаны в первом столбце справа от вертикальной черты, а город, через который проходит условно-оптимальный маршрут, обозначен 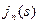 . Рекуррентное соотношение для
. Рекуррентное соотношение для 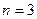 имеет вид
имеет вид 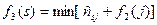 .
.
Отметим, что для подсчёта условно-оптимальных значений используется значение 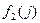 , полученное на предыдущем шаге, из таблицы 6.5. Вычисление для третьего шага [
, полученное на предыдущем шаге, из таблицы 6.5. Вычисление для третьего шага [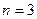 ,
,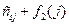 ] приведены в таблице 6.6. Здесь две клетки заштрихованы, поскольку из городов 2 и 3 нельзя попасть в город 7.
] приведены в таблице 6.6. Здесь две клетки заштрихованы, поскольку из городов 2 и 3 нельзя попасть в город 7.
Вычисления для четвертого шага [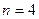 ,
, 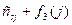 ] приведены в таблице 6.7.
] приведены в таблице 6.7.
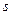
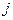
|
|
|
| 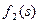
| 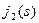
|
|
| 3+11
| 4+8
| -
|
|
|
|
| 1+11
| 6+8
| -
|
|
|
|
| 4+11
| 6+8
| 4+12
|
|
|
таблица 6.6
таблица 6.7
Из таблицы 6.7 видно, что минимальные затраты на перевозку груза 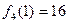 и оптимальный маршрут проходит через город 2, так как
и оптимальный маршрут проходит через город 2, так как 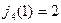 . Далее из таблицы 6.6 при
. Далее из таблицы 6.6 при 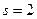 следует, что оптимальный маршрут проходит через город 6, так как
следует, что оптимальный маршрут проходит через город 6, так как 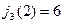 . Продолжая рассмотрение таблиц, для
. Продолжая рассмотрение таблиц, для 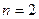 определяем, что оптимальный маршрут проходит через город 9 (
определяем, что оптимальный маршрут проходит через город 9 (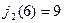 ). Наконец, из города 9 груз доставляется в конечный город 10 (место назначения). Таким образом двигаясь от последней таблицы к первой, мы определили оптимальный маршрут
). Наконец, из города 9 груз доставляется в конечный город 10 (место назначения). Таким образом двигаясь от последней таблицы к первой, мы определили оптимальный маршрут 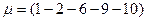 , затраты на перевозку груза по которому составляют
, затраты на перевозку груза по которому составляют 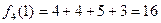 .
.

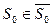 и являющаяся управляемой. Таким образом при осуществлении некоторого управления
и являющаяся управляемой. Таким образом при осуществлении некоторого управления 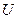 система переходит из состояния
система переходит из состояния 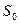 в конечное состояние
в конечное состояние 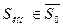 . При этом качество каждого из реализуемых управление
. При этом качество каждого из реализуемых управление 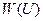 .
.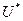 , чтобы функция
, чтобы функция 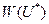 принимала свое максимальное или минимальное значение. Данная задача является общей задачей динамического программирования.
принимала свое максимальное или минимальное значение. Данная задача является общей задачей динамического программирования.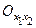

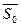 в область конечных состояний Каждому управлению
в область конечных состояний Каждому управлению 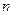 - мерного пространства).
- мерного пространства).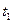 ,
,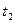 ,...,
,...,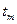 распределяются между предприятиями. Одновременно с этим между предприятиями распределяется полученная или за прошлый год прибыль. Таким образом в начале каждого
распределяются между предприятиями. Одновременно с этим между предприятиями распределяется полученная или за прошлый год прибыль. Таким образом в начале каждого 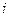 -года рассматриваемого периода
-года рассматриваемого периода 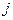 предприятие получает в свое распоряжение
предприятие получает в свое распоряжение 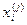 тысяч у.е.
тысяч у.е.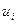 . Таким образом
. Таким образом 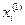 , второму -
, второму - 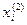 ,...,
,..., 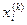 .
.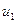 ,
, 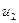 ,…,
,…,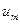 на
на 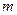 -шагов распределения средств как
-шагов распределения средств как 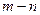 - мерного пространства.
- мерного пространства.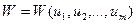
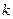 -ом шаге определяется совокупность чисел
-ом шаге определяется совокупность чисел 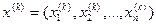 , полученных в результате управления
, полученных в результате управления 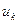 . Данные управления обеспечивают переход системы из состояния
. Данные управления обеспечивают переход системы из состояния 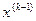 в
в 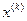 . При этом считается , что состояние
. При этом считается , что состояние 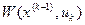 тогда общий доход или выигрыш за
тогда общий доход или выигрыш за 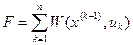
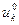 , выбранное при определенных добавлениях и предположениях о том, как значение предыдущий шаг называется условно оптимальным управлением.
, выбранное при определенных добавлениях и предположениях о том, как значение предыдущий шаг называется условно оптимальным управлением.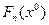 — это максимальный доход, полученный за
— это максимальный доход, полученный за 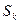 из начального состояния
из начального состояния 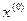 в конечное состояние
в конечное состояние 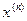 .
.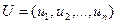 . Пусть
. Пусть 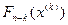 — это максимальный доход, получаемый при переходе системы из состояния
— это максимальный доход, получаемый при переходе системы из состояния 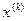 в конечное состояние
в конечное состояние 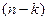 шагов. Тогда можно записать след:
шагов. Тогда можно записать след: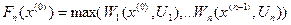
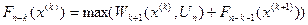 ,
, 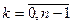
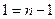 ):
):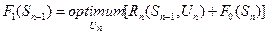
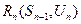 из дискретного набора его значений при некоторых фиксированных
из дискретного набора его значений при некоторых фиксированных 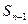 и
и 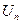 из соответствующих допустимых областей (так как
из соответствующих допустимых областей (так как 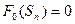 , то
, то 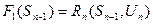 . В результате после первого шага известно решение
. В результате после первого шага известно решение 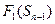 ;
;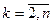 ) оно имеет вид
) оно имеет вид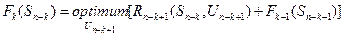 ; (6.2)
; (6.2)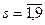 ) в город
) в город 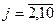 ) проставлена над соответствующими дугами сети. Необходимо найти маршрут , связывающий города А и В, для которого суммарные затраты на перевозку груза были бы наименьшими. На рис. 6.1. городам поставлены в соответствие вершины сети, обозначенные кружками с номером, а транспортным магистралям — дуги (линии со стрелками), соединяющие вершины.
) проставлена над соответствующими дугами сети. Необходимо найти маршрут , связывающий города А и В, для которого суммарные затраты на перевозку груза были бы наименьшими. На рис. 6.1. городам поставлены в соответствие вершины сети, обозначенные кружками с номером, а транспортным магистралям — дуги (линии со стрелками), соединяющие вершины.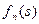 - минимальные затраты на перевозку груза от города s до конечного города, если до конечного города осталось
- минимальные затраты на перевозку груза от города s до конечного города, если до конечного города осталось 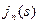 - номер города , через который нужно ехать из города s, чтобы досчитать
- номер города , через который нужно ехать из города s, чтобы досчитать 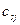 - - стоимость перевозки груза из города s в город
- - стоимость перевозки груза из города s в город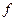 означает целевую функцию,
означает целевую функцию, 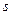 - состояние системы (номер города), индекс
- состояние системы (номер города), индекс 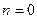 ) и
) и 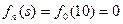 , так как из города s до конечного города осталось
, так как из города s до конечного города осталось 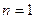 ) и вычислим для него значение функции. Очевидно, что в город 10 груз может быть доставлен или из города 8 ,или из города 9. Вычислим затраты на перевозку для этих двух состояний:
) и вычислим для него значение функции. Очевидно, что в город 10 груз может быть доставлен или из города 8 ,или из города 9. Вычислим затраты на перевозку для этих двух состояний: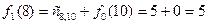 ,
, 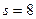 ,
, 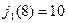 ;
;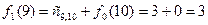 ,
, 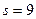 ,
, 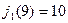 ;
;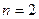 , выдвинем гипотезы о месте нахождения груза:
, выдвинем гипотезы о месте нахождения груза: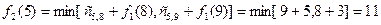

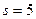 и
и 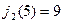 , т.е. условно-оптимальный маршрут проходит через город 9.
, т.е. условно-оптимальный маршрут проходит через город 9.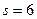 и
и 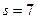 .
.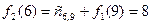
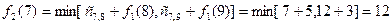
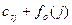 ] и второго [
] и второго [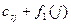 ] этапов помещены в табл.6.4 и 6.5 соответственно.
] этапов помещены в табл.6.4 и 6.5 соответственно.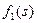
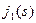
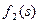
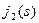
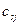 доставки груза из города s в город j и стоимости
доставки груза из города s в город j и стоимости 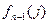 доставки груза от города
доставки груза от города 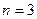 имеет вид
имеет вид 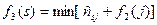 .
.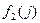 , полученное на предыдущем шаге, из таблицы 6.5. Вычисление для третьего шага [
, полученное на предыдущем шаге, из таблицы 6.5. Вычисление для третьего шага [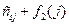 ] приведены в таблице 6.6. Здесь две клетки заштрихованы, поскольку из городов 2 и 3 нельзя попасть в город 7.
] приведены в таблице 6.6. Здесь две клетки заштрихованы, поскольку из городов 2 и 3 нельзя попасть в город 7.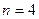 ,
, 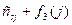 ] приведены в таблице 6.7.
] приведены в таблице 6.7.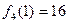 и оптимальный маршрут проходит через город 2, так как
и оптимальный маршрут проходит через город 2, так как 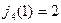 . Далее из таблицы 6.6 при
. Далее из таблицы 6.6 при 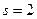 следует, что оптимальный маршрут проходит через город 6, так как
следует, что оптимальный маршрут проходит через город 6, так как 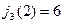 . Продолжая рассмотрение таблиц, для
. Продолжая рассмотрение таблиц, для 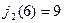 ). Наконец, из города 9 груз доставляется в конечный город 10 (место назначения). Таким образом двигаясь от последней таблицы к первой, мы определили оптимальный маршрут
). Наконец, из города 9 груз доставляется в конечный город 10 (место назначения). Таким образом двигаясь от последней таблицы к первой, мы определили оптимальный маршрут 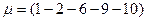 , затраты на перевозку груза по которому составляют
, затраты на перевозку груза по которому составляют 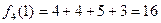 .
.