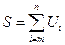Использование функций в качестве параметра

Идентификатор функции или процедуры может использоваться в качестве па­раметра другой функции. Если такая необходимость появилась, то требуется соот­ветствующим образом специфицировать каждый такой формальный параметр.

Спецификацией в этом случае являются: заголовок передаваемой функции, вклю­чающей имя функции, список формальных параметров и тип результата. Специ­фикация функции описывается в разделе TYPE следующим образом:

TYPE <имя спецификации> = FUNCTION(<список параметров>): <тип результата>;

Пример 48. В интервале [А, В] методом поразрядного приближения найти максимум функции

F(X) = 0.1Х³ – 2Х² + 10Х.

Формульно-словесный алгоритм метода состоит в следующем.

1. Задается начальное приближение Х₀= А слева от максимума F(X) и вычисля­ется F(X₀). Задается D = h, где h = ΔХ - начальный шаг поиска.

2. Полагаем G = F(X_n), где вначале F(X_n) = F(X₀), задаем X = X + D и вычисляем F(X_n+1)=F(X).

3. Проверяем условие F(X_n+1) > G; если оно выполняется, то идем к п. 2, если нет – к п. 4.

4. Полагаем D = –D/4. Проверяем условие | D | >Е/4, где Е — заданная погреш­ность вычисления Х_n в точке максимума. Если она выполняется, идем к п. 2, то есть обеспечиваем поиск максимума в другом направлении с шагом в четыре раза меньше прежнего. Если данное условие выполняется, заканчиваем счет, принимая за максимум X.

В этом известном алгоритме не учитывается тот факт, что в заданном интерва­ле [А, В] нет экстремума (максимума). В этом случае максимум будет на границе интервала либо в точке А, либо в точке В. Учитывая простоту функции F(X) и основ­ной программы, приведем структурограмму только функции PRP(A, В, Е, F), кото­рая осуществляет поиск максимума функции F в интервале [А, В] с погрешностью приближения Е.

Структурограмма функции PRP(A, В, Е, F)

N= 10; D= (В - A)/N; X = А;
Пока ABS(D) > Е делать:
		G = F(X); PRP = X; X = X + D;
		((X > В) OR (X < A)) AND (F(X) > G)   True
		EXIT {Выход по причине достижения максимума на границе интервала}
		PRP = X;
		До тех пор пока W(X) < G делать;
	D:=-D/4; {Изменить направление поиска и шаг уменьшить в 4 раза}

PROGRAM PR48;

TYPE FUN = FUNCTION(X: REAL):REAL; {Спецификация функции}

VAR X, А, В, E: REAL; N: INTEGER;

{$F+} {Директива. Компиляция функций с дальним типом обращения }

FUNCTION F(Z: REAL): REAL; {Исследуемая на экстремум функция}

BEGIN

F:=((0.1*Z-2)*Z+10)*Z

END;

FUNCTION PRP(A, В, E: REAL; W: FUN): REAL;

CONST N = 10; {Число участков, на которые разбивается [А, В]}

VAR I: INTEGER; D, G, X: REAL;

BEGIN

D := (В - A)/N; X := A; {D - шаг поиска}

WHILE ABS(D) > Е DO BEGIN REPEAT

G := W(X); PRP:=X; X := X + D;

IF ((X > B) OR (X < A)) AND (W(X) > G) {Максимум на границе интервала}

THEN EXIT; {Досрочное завершение функции}

PRP:=X;

UNTIL W(X) < G;

D := -D/4

END

END;

{$F-}

BEGIN

WRITELN('Укажите границы диапазона А, В'); READLN(A,B);

WRITELN('Задайте погрешность расчетов E'); READLN(E);

X := PRP(A, В, E, F); {Вычисление Xmax}

WRITELN('Xmax = ', X:11:9,’F(Xmax) =', F(X):13:9);

END.

Задав значения [А, В] = [2,3], E = 10^-9, получим X = 3,0; F(X) = 14.7. Очевидно, что экстремума в этом интервале нет, так как Х_max на границе интервала в точке В. Изменив исходные данные: [А, В] = [2, 5], Е = 10^-9, получим Х_max = 3,333332149; F(Х_max)= 14.814814815.

В теле функции использован оператор EXIT, который обеспечивает нормаль­ный выход из функции в том случае, когда нет экстремума и максимальное значе­ние — на границе интервала.

Замечание. Как правило, компилятор Паскаля автоматически подбира­ет метод адресации подпрограмм. Если подпрограмма находится в одном тексте с телом основной программы, то она компилируется с «ближним» (near) адресом вхо­да и возврата, содержащим только величину смещения адреса внутри текущего сег­мента памяти. Если подпрограмма находится в другом программном модуле, то генерируется «дальний» (far) адрес, содержащий адрес сегмента и смещения в сег­менте. При передаче имени функции в качестве программы необходим «дальний» адрес, но компилятор этого не понимает. Поэтому необходимо использовать ди­рективу компилятора {$F+}. Действие этой директивы распространяется на все под­программы, описанные ниже по тексту программы, или до директивы {$F-}.

Пример 49. Найти сумму

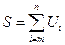
где U_i = F(i). Функция F(i) может быть различной: F₁(i) = 1/i; F₂(i) = i/(i + 1); F₃(i) = Cos (p/i).

При решении этой задачи следует помнить, что передача в качестве парамет­ров предопределенных (стандартных) функций, к которым относится и Cos(X), запрещена. Это ограничение обходится путем переопределения стандартной фун­кции в пользовательскую функцию.

PROGRAM PR49;

TYPE FUN = FUNCTION(A: INTEGER): REAL;

VAR S1: REAL; M, N, K: INTEGER;

{$F+}

FUNCTION F1(I: INTEGER): REAL;

BEGIN Fl := 1/I

END;

FUNCTION F2(I: INTEGER): REAL;

BEGIN F2:= I/(I+1)

END;

FUNCTION F3(I: INTEGER): REAL; { Переопределение функции COS }

BEGIN F3 := COS(PI/I)

END;

FUNCTION SUM(F : FUN): REAL;

VAR I: INTEGER;

S: REAL;

BEGIN

S:=0;

FOR I:=M TO N DO S := S + F(I); SUM:=S END;

{$F-}

BEGIN

WRITELN('Задайте M, N и номер функции (1, 2, 3)');

READ(M, N, К);

CASE К OF

1:S1:= SUM(Fl);

2: Sl:= SUM(F2);

3:S1:=SUM(F3)

END;

WRITELN('S = ',S1:8:5)

END.

Параметры M и N передаются в функцию SUM в качестве глобальных пере­менных. Фактическим параметром для этой функции является идентификатор одной из трех функций Fl, F2, F3.