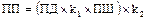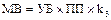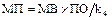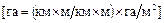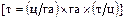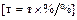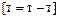В математике используют два способа решения задачи:
· аналитический;
· численный.
Аналитическое решение – получение функциональной зависимости (желательно оптимальной) выходного данного от входных.
Типичные примеры аналитического решения:
· зависимость 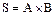 – для задачи нахождения площади прямоугольника S с длинами сторон A и B;
– для задачи нахождения площади прямоугольника S с длинами сторон A и B;
· зависимость 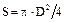 (
(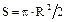 ) – для задачи нахождения площади круга в соответствии с конкретным входным данным (диаметром или радиусом).
) – для задачи нахождения площади круга в соответствии с конкретным входным данным (диаметром или радиусом).
Аналитические решения удобны профессионалам математикам.
Численное решение – получение конкретного значения выходного данного по известным значениям каждого из входных.
Наиболее простым и эффективным способом получения численного решения является подстановка конкретных значений входных данных в полученную ранее аналитическую зависимость и выполнение предписываемых ею действий. Численное решение удобно для пользователя непрофессионала.
Так, численное решение задачи нахождения площади прямоугольника при известных значениях входных величин (например, A = 25 м и B = 10 м), выполняется их подстановкой в аналитическое решение и имеет вид 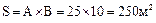 .
.
Для задачи о площади круга численное решение выполняется аналогично. Например, для известного значения диаметра (D = 3 см) значение площади 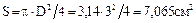 .
.
Расчетные зависимости – математические закономерности, связывающие разные виды и типы данных (выходные и входные) в соответствии с требованиями словесной формулировки задачи.
Сопоставив определение расчётных зависимостей и аналитического решения задачи можно сделать вывод:
ü Внимание ! Расчётные зависимости математической модели есть аналитическое решение задачи.
Расчетные зависимости формируются в результате детального изучения постановки задачи. Для каждой конкретной зависимости, при этом, возможна своя (требуемая) степень детализации.
Наименьшая степень детализации предполагает одну расчётную зависимость для решения всей задачи, т. е. представление искомого выходного данного (Двых) единой функцией от всех исходных(Двхi).
Двых = f(Двх1, Двх2, . . ., Двхi, . . ., Двхk)
В задаче о картофеле (пример 2.3) эта зависимость, например, имеет вид
МКВ = ((ПД 1000 ПШ/104) УБ/10) - ((ПД 1000 ПШ/104) УБ/10) ОП/100
Недостатки укрупненного варианта:
· сложность составления единой многокомпонентной функции;
· громоздкость записи;
· повторяемость некоторых участков;
· затруднённость проверки результатов решения задачи.
Увеличение степени детализации ликвидирует все (некоторые) указанные недостатки. При этом единая функциональная зависимость заменяется совокупностью нескольких взаимосвязанных (более простых).
Структуры создания расчётных зависимостей с максимальной степенью детализации имеют вид (табл. 2.2).
Таблица 2.2
| Универсальный вариант
| Простейший вариант
|
| П1 = f(Двх1, . . ., Двхk)
П2 = f(Двх1, . . ., Двхk, П1)
. . .
Пj = f(Двх1, . . ., Двхk, П1,. . ., Пj-1)
. . .
Двых = f(Двх1, . . ., Двхk, П1,. . ., Пj,. . .)
| П1 = f(Двх1, . . ., Двхk1)
П2 = f(Двхk2, . . ., Двхk3)
. . .
Пj = f(Двхki, . . ., Двхkk)
. . .
Двых = f(П1,. . ., Пj,. . .)
|
Характерная особенность рассмотренных структур – использование промежуточных данных (П1,. . ., Пj).
В принципе, наивысшая степень детализации достигается оформлением каждой расчётной зависимости в виде одной элементарной операции.
Недостатки такой детализации:
· увеличение объёма модели;
· снижение наглядности.
Выбор степени детализации характеризует степень квалификации разработчика. Модель можно считать оптимальной, если степень детализации обеспечивает приемлемый объём и наглядность, а также простоту отладки при решении и удобство анализа результатов.
ü Внимание ! При отсутствии чётких критериев для каждого промежуточного (конечного) данного рекомендуется степень детализации, обеспечивающая в расчётной зависимости 2 – 5 элементарных операций.
Конечные и промежуточные данные, в отличие от входных, могут быть только переменными. Их значения определяются в процессе решения в соответствии с расчётными зависимостями.
ü Внимание ! Математическая модель, в принципе, может состоять только из расчётных зависимостей, в правой части которых указаны конкретные значения входных данных. Однако, поскольку ММ является аналитическим решением задачи, её объекты должны быть модифицируемыми, т.е. задаваться в универсальном поименованном виде (обозначениями).
Следовательно, расчётные зависимости задачи о картофеле (пример 2.3) можно детализировано представить в двух вариантах:
| Конкретный вариант
| Универсальный вариант
|
| ПП = ПД x 1000 x ПШ/104
МВР = ПП x УБ/10
МКВ = МВР – МВР ОП/100
| ПП = ПД x k1 x ПШ/k2
МВР = ПП x УБ/k3
МКВ = МВР – МВР x ОП/k4
|
В предлагаемых вариантах данные ПП (поле, площадь) и МВР (масса выращенная) являются промежуточными. Коэффициенты 1000 (k1), 104 (k2), 10 (k3) и 100 (k4) в расчётных зависимостях позволяют получить промежуточные и конечные результаты нужных размерностей при планируемых исходных данных. Для большей универсальности математического описания во втором варианте они обозначены именами.
ü Внимание ! Дополнительные коэффициенты, введённые в расчётные зависимости, должны быть добавлены в раздел исходных данных с указанием конкретных значений и размерностей.
Получение расчётных зависимостей для математически сформулированных задач также трудностей не представляет и выполняется в соответствии с рассмотренными правилами. Так, для задачи расчёта значения функции y (пример 2.4) расчётные зависимости могут быть выполнены с различной степенью детализации. Например, представлены в виде:
 Выбранная степень детализации Увеличенная степень детализации
Выбранная степень детализации Увеличенная степень детализации

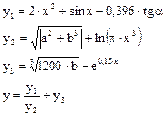
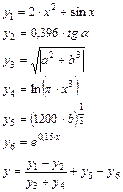
Степень детализации в левом варианте определялась желанием пользователя выделить основные компоненты заданной зависимости (числитель, знаменатель, второе слагаемое). Однако, выполнение таких укрупнённых компонентов не позволяет контролировать составляющие их элементы.
Правый вариант расчётных зависимостей частично устраняет этот недостаток. В принципе, детализация может быть увеличена до пооперационной, что естественно приведёт к существенному увеличению количества расчётных зависимостей.
Получение любой модели задачи должно заканчиваться проверкой на адекватность и универсальность.
Проверке на адекватность посвящены специальные разделы математики. В них достаточно подробно разработаны специальные методы оценки адекватности типовых задач. Простейшим из методов является проверка размерностей составленных расчётных зависимостей как внутри правой части, так и на соответствие левой.
ü Внимание ! Проверка соответствия размерностей обязательна для каждой расчётной зависимости модели.
Рассмотрение более сложных методик выходит за пределы данного раздела.
Обеспечение универсальности входит в обязанности разработчика математической модели. При этом действует правило, – чем универсальнее модель, тем она сложнее.
История развития математики условно делится на два этапа. На первом, докомпьютерном, из-за несовершенства средств реализации решения задач, использовались методы упрощения математических формулировок. На этом этапе были разработаны классические аналитические зависимости, широко используемые и в настоящее время. Например, вычисления площадей простейших фигур. Широкое внедрение ЭВМ показало, низкую универсальность классических зависимостей.
Один из способов увеличения универсальности – использование шаблонов задания значений входных данных. Под шаблоном будем понимать общий вид подразумеваемого численного (текстового) значения.
Структура шаблона:
_ _ . . . _[,]_ _ . . ._ [10 _ _]
, где _ – единичная цифра (символ) формируемого значения;
, – разделитель целой и дробной части (для вещественного числа);
10 – основание системы счисления;
[ ] – признак необязательности содержимого.
Например, запись
x = _ _
h = _ _,_ _ _
z = _ _,_ _ _ 10 _ _
предписывает, что данное x может принимать целое положительное значение от 1 до 99 или отрицательное от -1 до -9; данное h – любое значение от -9,999 до 99,999; данное z – любое значение указанное для данного h с учётом сомножителя 10 в степени с диапазоном от 10-9 до 1099.
Используем шаблоны для примера вычисления площади прямоугольника.
Классическая математическая модель задачи имеет вид:
Исходные данные
a = _ _ _,_ _
b = _ _ _,_ _
Расчётные зависимости
s = a * b
Анализ модели показывает:
· адекватность задаче достигается только в случае, когда размерности всех объектов задачи одинаковы;
· универсальность невысока и определяется возможностью выбора значения в диапазоне шаблона;
· использование данных разной размерности одновременно не предусмотрено, т.к. создатели зависимостей подразумевали мысленную работу пользователя по предварительной подготовке данных к использованию в расчёте.
Универсальность модели достигается применением вспомогательных данных (коэффициентов). Это позволяет получить вариант расчётной зависимости, пригодный для использования с любыми по размерности величинами.
Возможны несколько вариантов модернизации. Наиболее эффективным является следующий:
Исходные данные
| (основные)
| (вспомогательные)
|
| a = _ _ _,_ _
b = _ _ _,_ _
| k1 = _ _ _ _,_ _ _ _
k2 = _ _ _ _,_ _ _ _
|
Расчётная зависимость
s = (a * k1) * (b * k2)
Вспомогательные данные (k1, k2) позволяют привести значения (размерности) каждого основного входного данного к размерности выходного. При этом зависимость вычисления площади s работоспособна при любых (различных по размерности) значениях a и b.
Так, если a = 3 мм; b = 6,2 см и s требуется получить в квадратных метрах, достаточно присвоить коэффициенту k1 значение 0,001 м/мм, а коэффициенту k2 – значение 0,01 м/см.
При этом математическая модель может быть представлена вариантом:
Исходные данные
| (основные)
| (вспомогательные)
|
| a = 3 мм
b = 6,2 см
| k1 = 0,001 м/мм
k2 = 0,01 м/см
|
Расчётная зависимость
s = (a * k1) * (b * k2) [ м2 = (мм * м/мм) * (см * м/см) ]
Проверка размерностей доказывает правильность составленной расчётной зависимости.
ü Внимание ! Вспомогательные коэффициенты для уравнивания размерностей данных всегда размерны.
Аналогично рассмотренному, создадим универсальную модель вычисления площади круга.
Исходные данные
| (основные)
| (вспомогательные)
|
ЛР = _ _,_
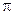 = 3,_ _ _ _ = 3,_ _ _ _
| k1 = _ _ _ _,_ _ _ _
k2 = _
|
Расчётная зависимость
s = (ЛР * k1)2 /k2
Полученная расчётная зависимость универсальна по размерности благодаря коэффициенту k1 и виду линейного размера ЛР (диаметр или радиус), определяющего значение коэффициента k2 (4 или 2).
Например, конкретная модель для вычисления площади в квадратных сантиметрах через радиус в дециметрах имеет вид:
Исходные данные
| (основные)
| (вспомогательные)
|
ЛР = 50,1 дм
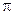 = 3,1416 = 3,1416
| k1 = 10 см/дм
k2 = 2
|
Расчётная зависимость
s = (ЛР * k1)2 /k2 [ cм2 = (дм * см/дм)2 / ]
Рассмотренные варианты представления данных и расчётных зависимостей позволяют сформулировать общие правила составления модели задачи.
Правила формирования математической модели.
· Выполнять модель задачи блочно (исходные данные, расчётные зависимости).
· Выбирать для каждого блока требуемую степень детализации
· Обозначать все участвующие в задаче данные именами, определяющими их суть, что облегчает понимание задачи другими пользователями.
· Указывать размерности всех используемых данных для контроля правильности планируемых вычислений.
· Записывать математические зависимости в универсальном виде, пригодном для решения множества аналогичных задач.
Выполним модель задачи о картофеле (пример 2.3) по изложенным правилам.
Вначале откорректируем используемые в словесной формулировке задачи наименования данных. Так, понятие «биологическая урожайность» изменим на «урожайность биологическая» (основное понятие – урожай). Следовательно, обозначение БУ модифицируются в УБ. Аналогично наименования «выращенный урожай», «общие потери», «товарная масса картофеля» заменим на «масса выращенная», «потери общие», «масса товарная» и обозначим МВ, ПО и МТ. Обозначение ДП (длина поля) запишем как ПД (поле, длина), а аббревиатуру ШП (ширина поля) – как ПШ (поле, ширина).
Следовательно, в качестве обозначений основных исходных данных приняты: ПД (поле, длина), ПШ (поле, ширина), УБ (урожайность биологическая), ПО (потери общие), выходного данного – МТ (масса товарная).
Полученные обозначения используем для составления универсальной модели задачи о картофеле (пример 2.3).
Исходные данные
| (основные)
|
|
| ПД = _ _ _,_ _
| – длина поля;
|
| ПШ = _ _ _,_ _
| – ширина поля;
|
| УБ = _ _ _,_ _ _
| – биологическая урожайность;
|
| ПО = _ _,_ _
| – общие потери;
|
| (вспомогательные)
|
|
| k1 = _ _ _ _,_ _ _ _
| – коэффициент выравнивания размерностей ширины и длины;
|
| k2 = _ _ _ _,_ _ _ _
| – коэффициент выравнивания размерности площади в уравнении;
|
| k3 = _ _ _ _,_ _ _ _
| – коэффициент выравнивания размерности массы;
|
| k4 = _ _ _
| – коэффициент преобразования процентов в доли единицы;
|
| | | |
Расчётные зависимости
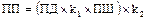
| – площадь поля;
|
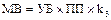
| – масса выращенная;
|
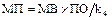
| – масса потерь;
|
| МТ = МВ – МП
| – масса товарная.
|
При составлении расчётных зависимостей возникла необходимость использования промежуточных данных для расчёта площади поля (ПП), массы выращенной (МВ), массы потерь (МП). Использование этих данных увеличивает степень детализации расчётов, облегчая в дальнейшем отладку решения и анализ его результатов.
Использование в математической формулировке именованных данных и шаблонов, позволило получить универсальную модель, пригодную для прямоугольных полей с любыми размерами, урожайностью, общими потерями.
Предложенная методика корректировки обозначений данных и создания математической модели пригодна для использования в задачах любых видов и типов.
Пример реализации универсального варианта модели задачи о картофеле с конкретными входными данными из словесной формулировки имеет вид:
Исходные данные
| ПД = 1,2 км
| – длина поля;
|
| ПШ = 750 м
| – ширина поля;
|
| УБ = 180 ц/га
| – биологическая урожайность;
|
| ПО = 12,7 %
| – общие потери.
|
| k1 = 1000 м/км
| – коэффициент выравнивания размерностей ширины и длины;
|
| k2 = 10-4 га/м2
| – коэффициент выравнивания размерности площади;
|
| k3 = 0,1 т/ц
| – коэффициент выравнивания размерности массы;
|
| k4 = 100 %
| – коэффициент преобразования процентов в доли единицы;
|
Расчётные зависимости
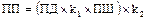
| 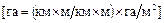
| – площадь поля;
|
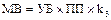
| 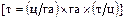
| – масса выращенная;
|
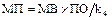
| 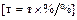
| – масса потерь;
|
| МТ = МВ – МП
| 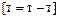
| – масса товарная.
|
Получение математической модели позволяет перейти к следующему этапу создания программного продукта – алгоритмизации.

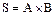 – для задачи нахождения площади прямоугольника S с длинами сторон A и B;
– для задачи нахождения площади прямоугольника S с длинами сторон A и B;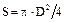 (
(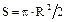 ) – для задачи нахождения площади круга в соответствии с конкретным входным данным (диаметром или радиусом).
) – для задачи нахождения площади круга в соответствии с конкретным входным данным (диаметром или радиусом).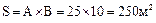 .
.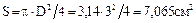 .
. Выбранная степень детализации Увеличенная степень детализации
Выбранная степень детализации Увеличенная степень детализации
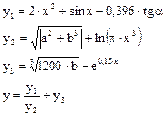
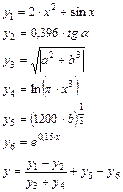
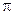 = 3,_ _ _ _
= 3,_ _ _ _