Наряду со словесной возможна математическая (формульная) постановка задачи.
Математическая постановка представляет собой конкретные зависимости вычисления искомых функций с указанием исходных данных.
Математическая формулировка может быть выполнена для всей задачи в целом или являться частью словесной.
В первом случае задача, как правило, чисто абстрактная. Входные данные могут задаваться отдельно или численными значениями в расчётных зависимостях. При этом они не имеют физической сути и, естественно, размерностей.
Рассмотрим две задачи с математической формулировкой.
Пример 1.4. Рассчитать значение функции
,
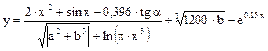если a=12; b= -9,2; x=2,75;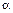 
=0,76.
Пример 1.5. Рассчитать корни квадратного уравнения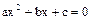 
по стандартной зависимости
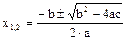, если a=1,4; b=11,2; c= -7,8.
В примере 2.4 формулировка практически полностью представлена одной математической зависимостью, в примере 2.5 – математическая формулировка является частью словесной.
Типичными примерами частично математически сформулированных, являются задачи расчета площадей (объемов) геометрических фигур.
Пример 1.6. Рассчитать площади круга (в см2) по известной зависимости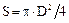 
, если диаметр изменяется от 35 см до 120 см с шагом 15 см.
Каждая из законченных постановок задач позволяет перейти к следующему этапу – созданию программного продукта.
