Наиболее сложным типом вычислительного процесса является циклический. Циклы возникают тогда, когда необходимо многократно повторять какие-либо действия. Число повторений в любом цикле должно быть конечным. Существуют циклы, в которых число повторений заранее известно (счетные циклы). В итерационных циклах количество повторений заранее неизвестно, выход из них осуществляется по достижению заданных условий.
Рассмотрим несколько примеров циклических процессов.
Пример 5. Найти конечную сумму S=1+1/2+1/3+….+1/n.
Введем следующие обозначения. Переменная i – номер слагаемого данной суммы. Само слагаемое имеет вид 1/i. Необходимо просмотреть все номера, начиная с первого и кончая последним номером n, и каждое слагаемое прибавить к S. Предлагается следующая схема алгоритма нахождения S.
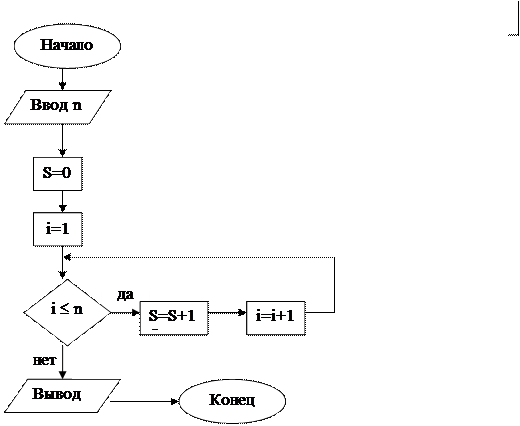
Рис.8.Схема алгоритма решения примера 5.
Рассмотрим еще один пример.
Пример 6. Дан массив чисел D=(d1,d2,..,dn). Найти dср по формуле
dср= (d1+d2+..+dn)/n.
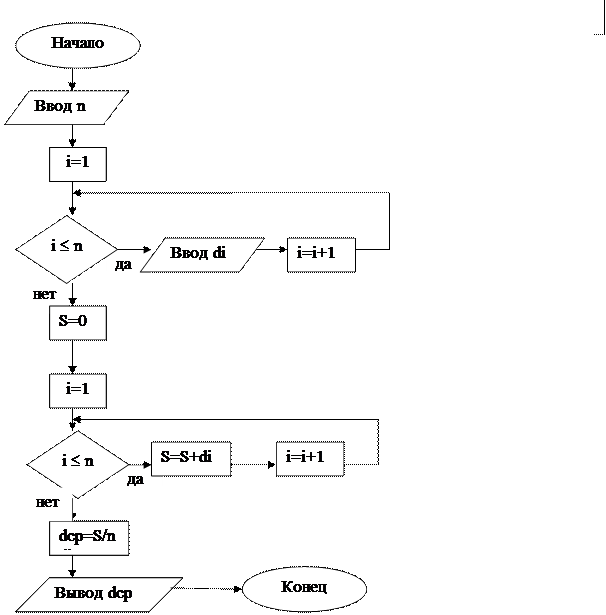
Рис.9.Схема алгоритма решения примера 6.
Решение этого примера похоже на решение предыдущего примера. Сначала введем исходные данные d1,d2,..,dn и найдем их сумму S. Разделив S на n, получим dср и выведем результат.