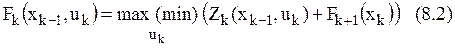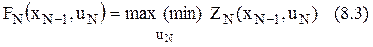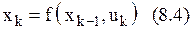Основные понятия.
Динамическое программирование (динамическое планирование) - метод нахождения оптимальных решений в задачах с многошаговой (многоэтапной) структурой.
Многие экономические процессы расчленяются на шаги естественным образом. Это все процессы планирования и управления, развиваемые во времени. Естественным шагом в них может быть год, квартал, месяц, декада, неделя, день и т. д. Однако метод динамического программирования может использоваться при решении задач, где время вообще не фигурирует; разделение на шаги в таких задачах вводится искусственно. Поэтому «динамика» задач динамического программирования заключается в методе решения.
Особенности задач динамического программирования.
1. Рассматривается система, состояние которой на каждом шаге определяется вектором xt. Дальнейшее изменение ее состояния зависит только от данного состояния хt и не зависит от того, каким путем система пришла в него. Такие процессы называются процессами без последействия.
2. На каждом шаге выбирается одно решение ut, под действием которого система переходит из предыдущего состояния xt-1 в новое xt.
3.Действие на каждом шаге связано с определенным выигрышем (доходом, прибылью) или потерей (издержками), которые зависят от состояния на начало шага (этапа) и принятого решения.
4.На векторы состояния и управления могут быть наложены ограничения (область допустимых решений).
5.Требуется найти такое допустимое управление ut для каждого шага t, чтобы получить экстремальное значение функции цели за все Т шагов.
Любую допустимую последовательность действий для каждого шага, переводящую систему из начального состояния в конечное, называют стратегией управления.
Допустимая стратегия управления, доставляющая функции цели экстремальное значение, называется оптимальной.
ПРИНЦИПЫ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Принцип оптимальности и погружения. Любую многошаговую задачу можно решать по-разному. Один из путей основан на идее проведения оптимизации поэтапно.
Сложную задачу разбиваем на ряд более простых. На каждом шаге оптимизируется задача малого размера, что уже нетрудно. При этом принцип динамического программирования вовсе не предполагает, что каждый шаг оптимизируется изолированно, независимо от других. Напротив, пошаговое управление должно выбираться с учетом всех его последствий.
Среди всех шагов существует один, который может планироваться без оглядки на будущее. Это последний шаг. Он может быть изучен и спланирован сам по себе наилучшим (в смысле выбранного критерия) образом, поскольку за ним нет больше этапов. Отсюда получаем одну из специфических особенностей динамического программирования: всю вычислительную процедуру программирования целесообразно разворачивать от конца к началу. Раньше всех планируется последний
N-й шаг, за ним (N—1)-й и т. д.
Но как найти оптимальное управление uN на N-м шаге, если оно определяется не только целью управления, но и состоянием системы на начало этого шага? Сделать это можно на основе предположений об ожидаемых исходах предшествующего, но еще не исследованного этапа, т. е. о значениях xN-1. Для каждого возможного исхода xN-1 на (N-1)-м этапе находим оптимальное управление на N-m этапе.
Такой набор оптимальных управлений, зависящих от возможных исходов предыдущего этапа, называется условно-оптимальным решением 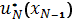 .
.
Завершив анализ конечного этапа, рассматривают аналогичную задачу для предпоследнего этапа, требуя, чтобы функция цели достигала экстремального значения на двух последних этапах вместе. Это дает условно-оптимальное решение на предпоследнем этапе 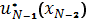 .
.
Проделав такой поиск условно-оптимальных управлений для каждого шага от конца к началу, найдем последовательность условно-оптимальных управлений 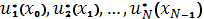 . Условно-оптимальные управления дают возможность найти не условное, а просто оптимальное управление на каждом шаге.
. Условно-оптимальные управления дают возможность найти не условное, а просто оптимальное управление на каждом шаге.
Проделав обратное движение по условно-оптимальным управлениям от начала к концу, найдем просто оптимальные управления для всех этапов.
Таким образом, в процессе оптимизации управления методом динамического программирования многошаговый процесс проходится дважды. Первый раз — от конца к началу, в результате чего находятся условно-оптимальные управления и условно-оптимальное значение функции цели для каждого шага, в том числе оптимальное управление для первого шага и оптимальное значение функции цели для всего процесса. Второй раз — от начала к концу, в результате чего находятся уже оптимальные управления на каждом шаге с точки зрения всего процесса.
Принцип оптимальности. Оптимальное управление на каждом шаге определяется состоянием системы на начало этого шага и целью управления.
Принцип погружения. Природа задачи, допускающей использование метода динамического программирования, не меняется при изменении количества шагов N. В этом смысле всякий конкретный процесс с заданным числом шагов оказывается как бы погруженным в семейство подобных ему процессов и может рассматриваться с позиции более широкого класса задач.
РЕШЕНИЕ ЭКОНОМИЧЕСКИХ ЗАДАЧ МЕТОДОМ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Пример 8.1 (задача о минимизации расхода горючего). Пусть самолет летит со скоростью v0 иа высоте h0. Он должен подняться на высоту hk, изменив скорость до vk- Известен расход горючего при подъеме самолета с любой высоты hi на любую высоту 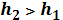 при постоянной скорости, а также расход горючего при увеличении скорости от любого значения vi до любого значения
при постоянной скорости, а также расход горючего при увеличении скорости от любого значения vi до любого значения 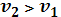 . Требуется найти оптимальное управление набором высоты и скорости, при котором общий расход горючего минимален.
. Требуется найти оптимальное управление набором высоты и скорости, при котором общий расход горючего минимален.
Пример 8.2. (задача выбора кратчайшего пути). Задана транспортная сеть, на которой указаны пункт отправления А и пункт назначения В (рис. 8.5). Между ними имеется много других пунктов. Некоторые соединены между собой участками пути. Над каждым участком транспортной сети поставлены цифры, указывающие расстояния между 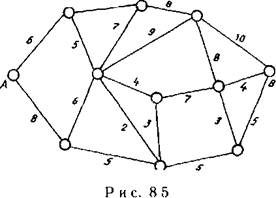 /о
/о
данными пунктами. Требуется составить маршрут минимальной длины из пункта A в пункт В
В экономической практике встречается несколько типов задач, которые по постановке или способу решения относятся к задачам динамического программирования.
1) Задача перспективного планирования. Планируется деятельность группы N промышленных предприятий Пi 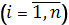 на период в t
на период в t 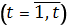 хозяйственных лет.
хозяйственных лет.
В начале периода на развитие системы предприятий выделены какие-то средства К, которые должны быть распределены между предприятиями.
В процессе деятельности предприятия вложенные в него средства частично амортизируются.
Каждое предприятие за год приносит доход, зависящий от вложенных средств, часть которого отчисляется в фонд предприятий.
В начале каждого хозяйственного года имеющиеся средства перераспределяются между предприятиями.
Определить объем средств в начале каждого года, которые нужно выделить каждому предприятию, чтобы суммарный чистый доход за Т лет был максимальным.
Это типичная задача динамического программирования. Здесь процесс принятия решения разбивается на Т шагов. Управление им заключается в начальном распределении и последующих перераспределениях средств 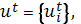 где
где 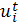 — объем средств, выделенных i-му предприятию в начале t-го года.
— объем средств, выделенных i-му предприятию в начале t-го года.
Для описания динамики системы вводится вектор состояния 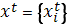 , где x— состояние i-го предприятия на начало t-ro года. В свою очередь состояние каждого предприятия
, где x— состояние i-го предприятия на начало t-ro года. В свою очередь состояние каждого предприятия 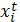 - является вектором, компонентами которого служат трудовые ресурсы, основные фонды, финансовое положение и т. д., т. е.
- является вектором, компонентами которого служат трудовые ресурсы, основные фонды, финансовое положение и т. д., т. е. 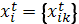 . Вектор управления — это функция состояния системы на начало соответствующего года:
. Вектор управления — это функция состояния системы на начало соответствующего года: 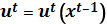 . Начальное состояние системы х0 может быть заданным. Целевой функцией будет суммарная прибыль объединения за Т лет. Если zt— прибыль за t-й год, то получим задачу
. Начальное состояние системы х0 может быть заданным. Целевой функцией будет суммарная прибыль объединения за Т лет. Если zt— прибыль за t-й год, то получим задачу
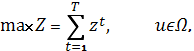
где 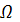 — область допустимых управлений, или множество экономических возможностей, определяемых различными ограничениями, налагаемыми на состояние системы и вектор управления.
— область допустимых управлений, или множество экономических возможностей, определяемых различными ограничениями, налагаемыми на состояние системы и вектор управления.
2) Задача об оптимальном управлении поставками.
С размещением заказов связаны некоторые фиксированные затраты К, не зависящие от величины заказываемой партии, а зависящие только от факта заказывания.
С содержанием материальных ресурсов связаны затраты, пропорциональные остатку нереализованной продукции на конец интервала.
Пусть Т — промежуток планирования.
vt - интенсивность потребления ресурса в t-м интервале.
Состояние системы будем описывать величиной остатка нереализованной продукции на конец интервала xt
Начальное х0 и конечное хT состояния системы можно считать заданными.
Для бесперебойности потребления поставками нужно управлять. Обозначим через 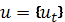 вектор управления, координаты которого суть величины поставок в начале соответствующих интервалов. Очевидно, что вектор управления есть функция состояния на начало интервала. Из множества возможных управлений требуется выбрать такое, при котором достигается минимум издержек на заказывание и содержание материальных ресурсов. Если St — издержки содержания единицы продукции в t-м интервале, то функция цели примет вид
вектор управления, координаты которого суть величины поставок в начале соответствующих интервалов. Очевидно, что вектор управления есть функция состояния на начало интервала. Из множества возможных управлений требуется выбрать такое, при котором достигается минимум издержек на заказывание и содержание материальных ресурсов. Если St — издержки содержания единицы продукции в t-м интервале, то функция цели примет вид
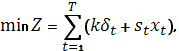
где 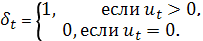
Состояние системы опишется соотношением 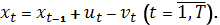 На состояние системы может быть наложено ограничение, связанное с надежностью снабжения:
На состояние системы может быть наложено ограничение, связанное с надежностью снабжения: 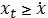 , где
, где 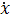 — величина некоторого страхового запаса, гарантирующего с заданной надежностью от сбоев в системе. Объединение ограничений, налагаемых на состояние системы и вектор управления, обозначим через Ω. Получим задачу
— величина некоторого страхового запаса, гарантирующего с заданной надежностью от сбоев в системе. Объединение ограничений, налагаемых на состояние системы и вектор управления, обозначим через Ω. Получим задачу
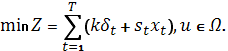
ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ БЕЛЛМАНА
http://www.matburo.ru/ex_mp.php?p1=mpdp
Дадим математическую формулировку принципа оптимальности Беллманадля задач с аддитивным критерием оптимальности (сепарабельная функция цели): каково бы ни было состояние системы S в результате (k-1) шагов, управление на k-м шаге должно выбираться так, чтобы оно в совокупности с управлениями на всех последующих шагах с (k+1)-го до N-го включительно доставляло экстремум целевой функции.
Обозначим:
х0, хN - начальное и конечное состояния системы.
uk - управление, которое может быть выбрано на k-м шаге и под воздействием которого система S переходит в состояние xk.
zk(хk-1,uk) - значение целевой функции на k-м шаге при управлении uk и при условии, что перед k-м шагом система находилась в состоянии хk-1.
Fk(хk-1,uk) - условно-оптимальное значение целевой функции на интервале от k-го до N-го шага включительно при условии, что перед k-м шагом система S находилась в состоянии xk-1, а на k-м шаге было выбрано управление uk.
Fk+1(хk) - условно-оптимальное значение целевой функции на интервале от (k+1)-го до N-го шага включительно при условии, что в результате воздействия условно-оптимального управления система S на k-м шаге перейдет к концу этого шага из состояния xk-1 в состояние xk.
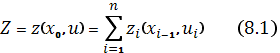
Надо найти оптимальное управление 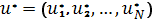 , такое, что доставляет экстремум целевой функции (8.1) при ограничениях uÎW.
, такое, что доставляет экстремум целевой функции (8.1) при ограничениях uÎW.
Принцип оптимальности Беллмана:
Основное функциональное уравнение ДП:
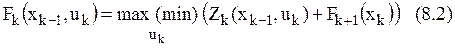
Для последнего N-го шага:
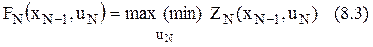
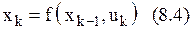
Состояние системы в конце k-го шага:
Уравнения Беллмана имеют рекуррентный (возвратный) характер, т.е. для нахождения оптимального управления на N шагах нужно знать условно-оптимальное управление на предшествующих N-1 этапах и т.д. Поэтому функциональные уравнения часто называют рекуррентными (возвратными) соотношениями Беллмана.
Строится вычислительная процедура метода ДП, распадающаяся на 2 этапа: условной и безусловной оптимизации.
1) Условная оптимизация: попятное движение от последнего шага к первому. С помощью уравнения (8.3) для каждого состояния xN-1 находится такое управление uN, при котором FN(xN-1,uN) достигает экстремума и система переходит в конечное состояние. Итак, для каждого состояния xN-1 находится условно-оптимальное значение целевой функции и соответствующее условно-оптимальное управление.
На основании (8.2) и состояния системы S перед (N-1)-м шагом определяется условно-оптимальное управление на (N-1)-м шаге и условно-оптимальное значение целевой функции на двух последних шагах (N-1)-м и N-м.
На основании (8.4) находится и состояние системы S перед N-м шагом, по которому с учетом предшествующих расчетов определяется условно-оптимальное значение FN(xN-1) целевой функции.
Продолжая процесс подобным образом, доходят до первого шага.
2) Безусловная оптимизация.
Для определения безусловно-оптимального управления системой при заданном начальном состоянии x0 анализируются выполненные расчеты при перемещении от 1-го шага к N-му. В результате находим экстремальное значение Z и оптимальное управление u*.
Пример 8.3 (задача распределения ресурсов). Двум предприятиям выделена на три года сумма X0=300 д.ед. От суммы X, выделенной предприятию П1, получают доход f1(X) = 5X, а от суммы X, выделенной предприятию П2 - доход f2(X) = 4X. В конце года возвращаются неиспользуемые средства в количествах: от предприятия П1 - 0,2X, от предприятия П2 - 0,5X, которые снова перераспределяются между предприятиями (доход им не возвращается). Найти оптимальное (по доходу) распределение средств по годам и предприятиям.
Пример 8.4 (задача о замене оборудования) Задача о замене оборудования (обновлении, восстановлении, перестройке) имеет важное значение. Рассмотрим ее в упрощенной постановке Известно, что оборудование со временем изнашивается, стареет физически и морально В процессе эксплуатации, как правило, падает его производительность и растут эксплуатационные расходы на текущий ремонт Со временем возникает необходимость замены оборудования, так как его дальнейшая эксплуатация обходится дороже, чем ремонт или замена. Отсюда задача о замене может быть сформулирована так. В процессе работы оборудование дает ежегодно прибыль, требует эксплуатационных затрат и имеет остаточную стоимость. Эти характеристики зависят от возраста оборудования В любом году оборудование можно сохранить, продать по оста точной цене и приобрести новое В случае сохранения оборудования возрастают эксплуатационные расходы и понижается производительность При замене нужны значительные дополнительные капитальные вложения Задача состоит в определении оптимальной стратегии замен в плановом периоде с тем, чтобы суммарная прибыль за этот период была максимальной

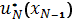 .
.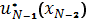 .
.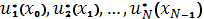 . Условно-оптимальные управления дают возможность найти не условное, а просто оптимальное управление на каждом шаге.
. Условно-оптимальные управления дают возможность найти не условное, а просто оптимальное управление на каждом шаге.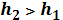 при постоянной скорости, а также расход горючего при увеличении скорости от любого значения vi до любого значения
при постоянной скорости, а также расход горючего при увеличении скорости от любого значения vi до любого значения 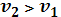 . Требуется найти оптимальное управление набором высоты и скорости, при котором общий расход горючего минимален.
. Требуется найти оптимальное управление набором высоты и скорости, при котором общий расход горючего минимален. /о
/о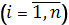 на период в t
на период в t 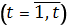 хозяйственных лет.
хозяйственных лет.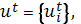 где
где 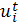 — объем средств, выделенных i-му предприятию в начале t-го года.
— объем средств, выделенных i-му предприятию в начале t-го года.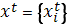 , где x— состояние i-го предприятия на начало t-ro года. В свою очередь состояние каждого предприятия
, где x— состояние i-го предприятия на начало t-ro года. В свою очередь состояние каждого предприятия 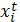 - является вектором, компонентами которого служат трудовые ресурсы, основные фонды, финансовое положение и т. д., т. е.
- является вектором, компонентами которого служат трудовые ресурсы, основные фонды, финансовое положение и т. д., т. е. 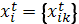 . Вектор управления — это функция состояния системы на начало соответствующего года:
. Вектор управления — это функция состояния системы на начало соответствующего года: 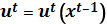 . Начальное состояние системы х0 может быть заданным. Целевой функцией будет суммарная прибыль объединения за Т лет. Если zt— прибыль за t-й год, то получим задачу
. Начальное состояние системы х0 может быть заданным. Целевой функцией будет суммарная прибыль объединения за Т лет. Если zt— прибыль за t-й год, то получим задачу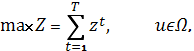
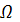 — область допустимых управлений, или множество экономических возможностей, определяемых различными ограничениями, налагаемыми на состояние системы и вектор управления.
— область допустимых управлений, или множество экономических возможностей, определяемых различными ограничениями, налагаемыми на состояние системы и вектор управления.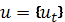 вектор управления, координаты которого суть величины поставок в начале соответствующих интервалов. Очевидно, что вектор управления есть функция состояния на начало интервала. Из множества возможных управлений требуется выбрать такое, при котором достигается минимум издержек на заказывание и содержание материальных ресурсов. Если St — издержки содержания единицы продукции в t-м интервале, то функция цели примет вид
вектор управления, координаты которого суть величины поставок в начале соответствующих интервалов. Очевидно, что вектор управления есть функция состояния на начало интервала. Из множества возможных управлений требуется выбрать такое, при котором достигается минимум издержек на заказывание и содержание материальных ресурсов. Если St — издержки содержания единицы продукции в t-м интервале, то функция цели примет вид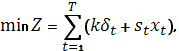
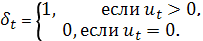
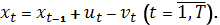 На состояние системы может быть наложено ограничение, связанное с надежностью снабжения:
На состояние системы может быть наложено ограничение, связанное с надежностью снабжения: 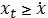 , где
, где 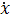 — величина некоторого страхового запаса, гарантирующего с заданной надежностью от сбоев в системе. Объединение ограничений, налагаемых на состояние системы и вектор управления, обозначим через Ω. Получим задачу
— величина некоторого страхового запаса, гарантирующего с заданной надежностью от сбоев в системе. Объединение ограничений, налагаемых на состояние системы и вектор управления, обозначим через Ω. Получим задачу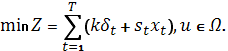
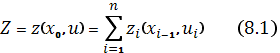
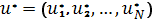 , такое, что доставляет экстремум целевой функции (8.1) при ограничениях uÎW.
, такое, что доставляет экстремум целевой функции (8.1) при ограничениях uÎW.