Любая мера информативности обязательно базируется на понятии вероятности, которое в каждом отдельном случае можно понимать по разному. Поэтому, прежде чем переходить непосредственно к изучению количественных мер информации, необходимо рассмотреть различные концепции вероятности и проанализировать их взаимосвязи.
Понятие вероятности неоднозначно. К его определению существует несколько различных подходов. Практическое значение имеют в основном них: частотный, логический и субъективный.
Наиболее широко распространена концепция объективной вероятности (частотный подход). На ней, как правило, базируются все учебные курсы вероятности и ее приложений. Концепция объективной вероятности применима к массовым явлениям и основывается на предпосылке существования объективной характеристики массового явления, которая носит название вероятности и приближенно измеряется частотой.
Пусть имеется бесконечная последовательность исходов испытаний Е1,Е2,…, Еп, обладающая свойством иррегулярности, т.е. отсутствием закономерности появления исходов в данной последовательности. Иррегулярность означает относительную независимость, относительную автономность элементов последовательности. И пусть событие А - некоторое множество из совокупности испытаний, а nA - число появлений события А в п испытаниях.
Тогда 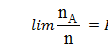 существует и называется вероятностью события A относительно данной совокупности.
существует и называется вероятностью события A относительно данной совокупности.
Таким образом, если считать, как это часто делают, что концептом объективной вероятности является единственно возможной, то окажется, что понятие вероятности применимо лишь к массовым явлениям, повторяющимся очень много раз.
Однако концепция объективной вероятности не является ни единственно возможной, ни даже в какой-либо степени привилегированной по сравнению с другими.
В управлении производством, да и, практически, в любой области деятельности, при принятии наиболее важных, сложных решений приходится делать заключение от известного к неизвестному. Такой способ умозаключения называется индукцией. Если определить неопределенность как незнание достоверного, то можно сказать, что человек постоянно имеет дело с индукцией, преодолевая неопределенность. Индукция изучается индуктивной логикой, являющейся одним из разделов формальной логики. В 17-18 веках Бэкон и Милль создали так называемую классическую индуктивную логику, которая пользовалась естественным языком. В 20 веке началась формализация индуктивной логики и понятие математической вероятности было тем понятием, которое для этого использовалось. Индуктивная логика стала логикой вероятностной, т.е. логикой, приписывающей высказываниям не только значение истинности или лжи, а и промежуточные значения, которые она называет вероятностями истинности высказываний.
Обозначим какую-либо гипотезу (высказывание) через 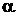 , а данные сведения, на которых эта гипотеза основывается, через
, а данные сведения, на которых эта гипотеза основывается, через 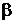 . Ясно, что между высказыванием
. Ясно, что между высказыванием 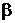 и высказыванием (гипотезой)
и высказыванием (гипотезой) 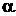 существует определенное логическое отношение. Высказывание
существует определенное логическое отношение. Высказывание 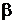 в той или иной степени подтверждает или делает вероятной гипотезу
в той или иной степени подтверждает или делает вероятной гипотезу 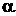 .
.
Мера связи суждения и достоверного знания, обусловленности первого вторым и называется логической вероятностью. 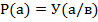
В настоящее время помимо рассмотренных двух концепций находит все большее признание и развитие, в основном в рампах так называемой теории решений, концепции субъективной вероятности. Рассмотрим понятие субъективной вероятности на некотором условном .примере.
Пусть Е - некоторое событие и пусть Р - та часть суммы S(ставки), которую дачный индивидуум согласен заплатить (S > 0) или получить (S < 0) за участие в пари, при котором он получает (платит) S в случае, если событие происходит. Пусть Е1,…,Еп - полная группа событий, т.е. одно Еiобязательно происходит и Еiне наступает одновременно, и пусть данным индивидуумом назначены соответствующие Рi . Если Si- сумма, которую получает (платит) индивидуум в случае, когда событие Еi произойдет, то
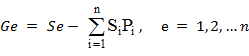
Будет суммарным выигрышем (или проигрышем в зависимости от знака) индивидуума от участия в n пари.
При условии когерентности (непротиворечивости) назначения, т.е. разумности поведения индивидуума, как нетрудно показать:
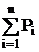 = 1
= 1
Величина Рi - степень личной уверенности данного индивидуума в совершении того или иного события и есть субъективные вероятности событий.
Следует заметить, что все три концепции не только не противоречат друг другу, но и весьма гармонично сочетаются между собой. Рассмотрим это на примере.
Допустим, следует оценить вероятность исхода какого-либо эксперимента. Дать такую оценку предлагают эксперту - человеку, имевшему дело с подобными экспериментами ранее. Его оценка и будет субъективной вероятностью данного исхода эксперимента. Необходимо подчеркнуть, что объективность данной оценки состоит лишь в том, что она несет на себе отражение личности эксперта: неполнота его знаний о всех подобных экспериментах и его личных психических особенностей. Основа же ее объективна. Это похожие случаи из практики эксперта, т.е. вполне достоверная информация о подобных ситуациях, случившихся ранее. Чем больше опыт эксперта в данной области, тем меньше в его оценке субъективного.
Предложив дать подобные оценки большой группе весьма сведущих в данном вопросе экспертов и рассчитав среднюю, мы сможем исчислить влияние индивидуальных особенностей экспертов на оценку и повысить степень ее достоверности за счет большей полноты, использования для прогноза знаний результатов похожих экспериментов в прошлом. Чем больше опыта, подходящего случаю, мы используем, тем ближе полученная оценка будет к индуктивной, логической вероятности.
Наконец, повторив названный эксперимент много раз и рассчитав частоту появления интересующего нас исхода, мы получим оценку объективной вероятности его, тем лучшую, чем большее число раз повторим эксперимент.
Нетрудно видеть, что в основе всех трех вероятностей исхода упомянутого эксперимента лежат вполне объективные вещи. В основе субъективной вероятности - личный опит индивидуума, его знание об исходах похожих экспериментов в прошлом. В основе логической вероятности - сведения о всех похожих экспериментах, накопленные данной отраслью знаний. В основе объективной (частотной) вероятности - знание исходов точно таких же экспериментов (а не похожих!), имевших место в прошлом.
Таким образом, логическая индуктивная вероятность является частным случаем субъективной, когда за счет привлечения дополнительного знания удается преодолеть ограниченность личной индивидуальной оценки. Объективная же вероятность является частным случаем логической (и, следовательно, субъективной), когда, многократным повторением эксперимента удается накопить достаточную информацию и получить хорошую оценку вероятности интересующего нас исхода. При этом ясно, что переход от одного вида вероятности к другому осуществляется вполне естественно за счет накопления количества и улучшения качества информации.
Важной особенностью концепций логической и субъективной вероятностей, в отличие от концепции объективной вероятности является рассмотрение проблемы вероятности индивидуального события. Это позволяет использовать мощный и хорошо разработанный аппарат математической теории вероятностей для значительно более широкого класса задач управления, чем это позволительно на базе концепции объективной вероятности.
Рассмотренные концепции по своей сути являются естественно-научными. Они объясняют природу, происхождение, физический смысл вероятности. Наряду с ними существует и математическая теория исчисления вероятностей, построенная на аксиоматике и не нуждающаяся в принципе ни в каком естественнонаучном объяснении. Указанная теория является общеприменимым математическим аппаратом для всех трех концепций вероятности.
При рассмотрении взаимосвязи трех концепций вероятности бросается в глаза, что их связь аналогична связи между собой трех разделов семиотики: синтактики, семантики и прагматики. Ниже мы убедимся, что такая аналогия не случайна, а имеет весьма глубокий теоретический я практический смысл.
Возникновение и развитие основных идей современной синтактики связано с так называемой теорией информации, которую более правильно следует называть статистической теорией связи. Теория связи зародилась вместе с телеграфией вследствие необходимости определения пропускной способности и загрузки различных систем связи. Специалисты, проектировавшие и эксплуатировавшие технические системы коммуникации, интересовались в первую очередь правильностью передачи сигналов, носителей сообщений. Их не интересовало, да и не могло интересовать содержание сообщений. В своей деятельности они исходили и исходят из того принципа, что если телеграф или телефон передают сигнала без искажения, общение будет обладать полезностью, истинностью, надежностью, новизной и всеми другими свойствами информации. Поэтому и математическая теория связи касается лишь самих сигналов и содержащегося в них «количества информации», абстрагируясь от всех специфических областей ее использования человеком.
Любой подход к измерению информации, в том числе и концепция Шеннона-Винера, связан с мерой неопределенности событий, которые происходят иди будут происходить.
Пусть имеет место некоторое событие А, следствием которого может быть n возможных исходов (а1, а2,…ап). Предположим, что каким-то образом можно оценить вероятность наступления каждого исхода: Р(а1), Р(а2),…,Р(ап). Допустим, что все исходы равновероятны.
Тогда 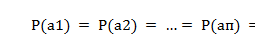
Если А может иметь только один исход (п = 1), то неопределенность события А равна нулю. При п = 2 она будет отлична от нуля и с возрастанием числа возможных исходов будет увеличиваться.
Рассмотрим сложное событие АВ, состоящее из двух независимых событий А и В. Событие А имеет п, а событие В – т равновероятных исходов.
Для удобства примем, что неопределенность сложного события равна сумме неопределенностей составляющих его простых событий. Однако событие АВ имеет пт равновероятностных исходов. В силу вышесказанного мера неопределенности сложного события должна удовлетворять условию:
У(пт) = У(п) + У(т)
Оказывается, что такому условию удовлетворяет лишь логарифмическая функция:
log(nm) = log(n) + log(m)
Таr как исходы предположены равновероятными, то очевидно, каждый из них будет вносить в общую неопределенность события равную долю, именно 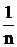 logn. Поскольку
logn. Поскольку 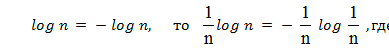 - вероятность каждого исхода. Следовательно, в общем случае неопределенность каждого исхода будет определяться лишь логарифмом его вероятности [- logP(ai)].
- вероятность каждого исхода. Следовательно, в общем случае неопределенность каждого исхода будет определяться лишь логарифмом его вероятности [- logP(ai)].
Так как информация есть мера устранения неопределенности, то ее естественно измерять как разность неопределенностей некоторого исхода до и после получения сообщения. Пусть неопределенность исхода до сообщения совершения события А измеряется logРо(ai), а после А - logРо(ai). Тогда количество информации об исходе ai, полученной из сообщения А, будет равно I(ai) = logР1(ai) - logРо(ai). Если это сообщение о совершении исхода ai, то Р1(ai) = 1 и I(ai) = - logРо(ai)
Из этого с очевидностью следует, что чей больше вероятность исхода до осуществления события (априорная вероятность); тем меньше количество информации, получаемое из сообщения о его осуществлении.
Выражение Iaiхарактеризует количество информации относительно индивидуального исхода ai . Но событие А может иметь несколько исходов. Ясно, что неопределенность каждого из них связана с неопределенностью события А в целом. Определим среднюю величину неопределенности всех возможных исходов, взвешенную по их вероятностям
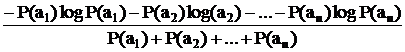 =Н(А)
=Н(А)
Н(А) = 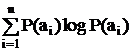
Величина Н(А) называется энтропией события А и является мерой его средней неопределенности. Нетрудно показать, что она достигает максимума при равновероятности всех исходов и делается тем меньшее, чем больше различия в вероятностях, отдельных исходов.
Энтропия сложного события (АВ) равна сумме энтропий составляющих его простых событий, но лишь при условии, что последние независимы Н(АВ) = Н(А) + Н(В). Если же А и В взаимосвязаны, то очевидно, что Н(АВ) < Н(А) + Н(В). В случае, когда исход события В полностью определяется исходом события А, т.е. если А и В связаны функциональной зависимостью Н(АВ) = Н(А). Если же зависимость, связывающая события А и В вероятностная, то Н(АВ) = Н(А) + Н(В/А), (п+1), где Н(В/А) - условная энтропия события В при условии, что событие А наступило.
Нетрудно видеть, что мера Шеннона-Винера является синтактической в самой своей основе, а вероятности, используете в ней, для измерения информативности сообщения суть объективные, частотные вероятности.
Сами создатели статистической теории связи И. Шеннон и Н. Винер неоднократно подчеркивали, что негэнтреция, как мера информативности безразлична к содержанию информации и к ее получателям. Этим во многом и объясняется ограниченная применимость меры Шеннона-Винера и бесплодность многочисленных попыток использовать ее где-либо вне рамок систем связи.
Поэтому естественно, что предпринимались многочисленные попытки построить другие системы измерения информации, более пригодные для использования в практике построения современных систем управления производством.
Известно несколько попыток, относящихся к возможностям введения количественной меры семантической информации. Интересным является то, что все они основывались на теории об индуктивной (логической) вероятности. Доказывается, что мера семантической информации Iiдолжна быть функцией логической вероятности утверждения. Если i и j - два высказывания и если Рi > Pj, то Ii < Ij . При этом под вероятностью понимается не относительная частота, а логическая вероятность.
Бар-Хиллел и Карнап, наиболее плодотворно работавшие в области построения теории семантической меры информации, сформулировали ряд теорем, касающихся информационного содержания высказывания. Оказалось что их теория во многих отношениях обнаруживает аналогию со статистической теорией связи Шеннона, однако между ними существуют и принципиальные различия.
Теория Шеннона описывает "количество информации" объективно, ограничиваясь рассмотрением знаков (сигналов) и статистических отношений между ними. Это синтактическая теория и как таковая входит составной частью в любую другую концепции информации. Рассматриваемые ею вероятности представляют собой относительные частоты знаков или их оценки (объективные вероятности).
Теория Бар-Хиллела и Карнапа - семантическая, но как таковая включает также и элементы синтактики. Бар-Хиллел показал, что теория связи Шеннона может быть полностью отображена в представлениях семантической теории, но не наоборот. Естественно, обе эти теории не рассматривают совершение конкретных использователей информации, их реакцию на эти знаки и т.п., то есть прагматические аспекты информации.
До сих пор не появилось какой-либо единой концепции прагматической меры информации. Однако некоторые попытки использовать для измерения ценности информации в рамках байесовской теории принятия решений оказались весьма плодотворными. Общий подход к измерению ценности информации удобно рассмотреть на примере, приведенном У. Моррисом в книге «Наука об управлении. Байесовский подход».
Имеется монета и специально изготовленная игральная кость, четыре стороны которой помечены словом «герб», а остальные две словом «решетка». Наблюдать бросание монеты и кости не разрешается. Один из предметов накрывается чашкой.
Пусть
То – «не накрыта монета»;
Т1 – «не накрыта кость»;
а – выпал «герб»;
в – выпала «решетка».
Если принимающий решение угадает правильно, какой именно предмет не накрыт, он получит приз 1 руб. В противном случае он не получает ничего. Вероятность событий То и Т1 на начало эксперимента предполагаются равными.
Р(То) = Р(Т1) = 1/2 Очевидно, что в этом случае ожидаемый выигрыш Со = 1/2 руб. Если же точно известно, какое событие произойдет, то ожидаемый ход (выигрыш) при наличии полной абсолютной надежной информации Спп = 1 руб.
Увеличение дохода руководителя по сравнению с доходом, который он получил бы на основе решений, принятых с помощью априорной информации, будем называть ожидаемой ценностью полной информации. В нашем примере Qnn = Cnn – Co = 1 – 0,5 = 0,5 руб.
Следовательно, максимальная сумма, которую имеет смысл заплатить за совершенно надежную информацию в нашем случае - 0,5 руб. Поскольку Qпп представляет собой прирост дохода от полного исключения неопределенности, эту величину иногда называют стоимостью неопределенности.
Попробуем теперь определить ценность неполной и выборочной информации. Для этого разовьем далее описанный выше пример с костью и монетой.
Лицо, производящее эксперимент, сообщает принимающему решение «гербом» или «решеткой» помечена верхняя сторона ненакрытого чашкой предмета. Ясно, что такое сообщение существенно повлияет на мнение принимающего решение о том, какой предмет накрыт чашкой. Интуитивно понятно, что при выпадении «герба» то, что не накрыта «кость» - более вероятно. Для количественной оценки степени устранения неопределенности используется теория Байеса, утверждающая, что условная вероятность события А , если известно, что событие В наступило, ровна словной вероятности события В при наступившем А, умноженной на безусловную вероятность события А и деленной на безусловную вероятность события В.
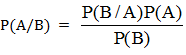
Предположим, что в нашем эксперименте не накрыта монета. Тогда условная вероятность события а: Р(а/То) = 1/2, если же не накрыта кость - событие Т, то Р(а/Т1) = 2/3.
В свою очередь Р(а) = Р(а/Т1)*Р(Т1) + Р(а/То)* Р(То) = 7/12
В соответствии с теоремой Байеса вероятность того, что накрыта кость, если известно, что выпал «герб», определится из выражения 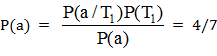 .
.
Аналогично Р(То/а) = 3/7. В свою очередь, условные вероятности событий То и Т1 после сообщения о том, что выпала «решетка» - апостериорные вероятности: Р(То/в) = 3/5; Р(Т1/в) =2/5. Соответственно, ожидаемый доход при догадке – «монета» на сообщение, что выпала «решетка» - 3/5 руб., а при догадке «кость» - 2/5 руб. Вероятности сообщений а и в равны 7/12 и 5/12. Ожидаемый доход при данной выборочной информации: Свп = 7/12*4/7 + 5/12*3/5 = 7/12 руб. Ожидаемая ценность выборочной информации в нашем случае: Qвп = 7/12 – 1/2 = 1/12 руб.

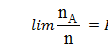 существует и называется вероятностью события A относительно данной совокупности.
существует и называется вероятностью события A относительно данной совокупности.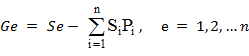
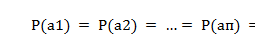
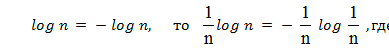 - вероятность каждого исхода. Следовательно, в общем случае неопределенность каждого исхода будет определяться лишь логарифмом его вероятности [- logP(ai)].
- вероятность каждого исхода. Следовательно, в общем случае неопределенность каждого исхода будет определяться лишь логарифмом его вероятности [- logP(ai)].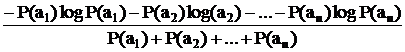 =Н(А)
=Н(А)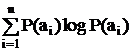
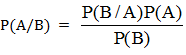
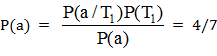 .
.