Преимущества многослойных сетей были поняты достаточно рано. Ясно было также, что для использования этих преимуществ, преобразование при переходе от одного слоя к другому должно быть нелинейным: последовательность линейных преобразований дает снова линейное преобразование со всеми его недостатками. Однако развитию многослойных сетей препятствовало то, что не было теоретически обоснованного алгоритма обучения таких сетей. Неясно было, по какому правилу следует модифицировать связи нейронов промежуточных слоев, чтобы получить на выходе нужный результат.
Такой алгоритм был предложен в ряде работ [74, 75]. Сейчас он известен как метод "обратного распространения ошибки". Этот метод частным случаем основного уравнения динамики.
Сущность его в следующем. Если известна целевая функция системы V(x), то можно найти силы, действующие на любые переменные системы и вызывающие их изменения в сторону максимизации целевой функции. Если эти переменные непосредственно входят в целевую функцию, то эти силы вычисляются по формуле (6.3). Таковы, например, выходные переменные системы, когда целевая функция непосредственно зависит только от них.
Если же интересующие переменные xi- непосредственно не входят в целевую функцию, но связаны с переменными xj-, входящими в нее, то действующие на xi силы могут быть вычислены с помощью "закона передачи силы"- обобщения известного закона рычага на немеханические системы. Закон, как известно, гласит: что выигрывается в силе (F), то проигрывается в расстоянии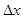 
. Это можно записать так:
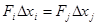F, или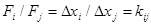 
Здесь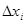 
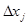- изменения двух связанных переменных; Fi, fj- действующие на них силы; kij - передаточный коэффициент от хi к хj..
В нейронных сетях к числу переменных, не входящих непосредственно в целевую функцию, относятся параметры нейронов промежуточных ("скрытых") слоев. Однако переменные i-го уровня связаны с переменными следующего j-го уровня. Передаточный коэффициент kijопределяется прежде всего весом синаптической связи cij. Так как если связь нелинейная, то в него должна входить сомножителем производная от активационной (передаточной) функции, зависящая от значения выходной переменной. Согласно закону передачи силы справедливо следующее соотношение между силами, действующими на выходные величины отyiиyjдвух соседних слоев:
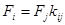
Подставляя сюда выражение для силы и для передаточного коэффициента и учитывая, что переменная одного слоя связана с несколькими переменными другого и что действующая на нее сила должна быть равнодействующей суммы сил, получаем слудующее рекуррентное соотношение, позволяющее находить производную n-1-го слоя по производной n-го слоя:
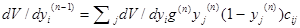
Зная силу, действующую на переменную, и используя основное уравнение динамики (6.4), можно написать закон изменения этой переменной. Если переменная- один из весовых коэффициентов cij- , то это и будет закон обучения.
В многослойных сетях, как правило, воздействие распространяется только в одном направлении - от i-го слоя к j-му. Следовательно, матрица связей несимметрична: только веса cij-, могут быть отличны от нуля, тогда как cji, заданы равными нулю.
Рассмотрим в качестве примера один из известных алгоритмов обучения - "?-правило". В простейшем виде оно использовалось уже при обучении персептрона. Суть его в следующем. Пусть в качестве желаемого ("идеального") значения выходной величины задано значение yj . Действительное значение y*j получается путем преобразования входных значений предыдущего слоя х и не обязательно совпадает с желаемым:
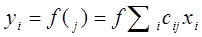
Здесь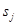 
- активационная функция; 
.
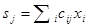Цель поведения состоит в минимизации квадрата ошибки:
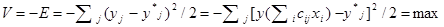
Тогда сила, действующая на переменную cji равна:
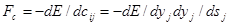
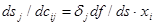
Здесь через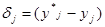 
обозначена разность между идеальным (желаемым) и действительным значениями выходной величины. Отсюда и название алгоритма-
?- правило. Скорость модификации веса определяется основным уравнением динамики в форме (6.5):
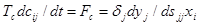
Это и есть ?-правило. Если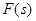 
- функция сигмоидального вида, то получается один из вариантов алгоритма обратного распространения ошибки:
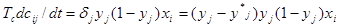(6.6)
Согласно этому алгоритму скорость модификации весового коэффициента cijпропорциональна трем факторам:
- "ошибке " - разности между действительным и желаемым значениями выходной величины
;
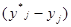- производной от функции активации
;
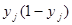- входной величине xt.
Если зависимость от первого фактора является полезной, то два последних фактора служат источником различного рода неприятностей, возникающих в процессе обучения.
В настоящее время обычно используют различные модификации этого алгоритма, имеющие целью улучшить устойчивость процесса обучения и разрешить ряд других проблем. Например, вводят в алгоритм "память " о предыдущем шаге, что придает ему определенную инерционность и устойчивость к помехам.
