Динамика обучения и поведения

В механике динамика в отличие от статики и кинематики предполагает наличие двух моментов: изменение переменных во времени и обусловленность этих изменений силами. Эти два момента имеют смысл применительно и к нейронным сетям. Сила здесь не просто метафора. Ей можно дать точное определение и количественное выражение. Это делает ее полезным инструментом для описания поведения системы. Но для этого сначала необходимо формально описать цель поведения системы.
При описании поведения системы одним из наиболее общих подходов [71] является обращение к экстремах принципам, когда цель поведения задается в виде стремления к максимуму или минимуму некоторой целевой функции (функционала потенциала):

V(x) = max .

Часто в роли такого потенциала выступает квадратичная функция от переменных, характеризующих систему ("энергия" Хопфилда, суммарный квадрат ошибки в методе обратного распространения и т.п.). Вид целевой функции наряду с конфигур сети является важнейшим фактором, определяющим характер поведения системы.

Определим обобщенную силу Fx действующую на переменyю x и ответственную за ее изменения, как частную производную от целевой функции по этой переменной:

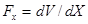                                                                                                                   (6.3)

Понятие силы удобно, потому что обычно оно определяется таким образом, что обладает свойством аддитивности. Пусть на одну переменную действует несколько факторов (например, она связана с несколькими другими переменными, как в нейросетях). Если необходимо определить результат их совместного действия, то слудует охарактеризовать эти факторы через силы и затем найти равнодействующую этих сил; вследствие аддитивности она будет равна векторной сумме этих сил.

В общем случае картина поведения вьглядит следующим образом: задаются целевая функция и условия, наложенные на переменные. В частности, некоторые переменные быть фиксированными. Тогда остальные свободные переменые начинают меняться в сторону увеличения целевой функции. Процесс продолжается до тех пор, пока не будет достигнут возможный в этих условиях максимум целевой функции (условный максимум). Поскольку поведение свободной переменной всегда направлено увеличение целевой функции, то для него справедливо следуещее выражение:

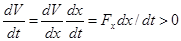
Отсюда следует, что знак обобщенной силы Fx и знак реакции dxldtв свободном поведении всегда совпадают: либо оба положительны, либо оба отрицательны - только так можно обеспечить положительность dVldt.

Таким образом, основное уравнение динамики системы, связывающее скорость изменения свободной переменной dxldtс действующей на нее силой Fx, можно написать в следующем виде:
 

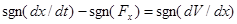
                                                                                                                                              (6.4)

Это уравнение является чрезвычайно общим. Все известные уравнения, описывающие процессы обучения или поведения нейросетей, являются его частными случаями и различаются между собой либо характером переменных, либо видом целевой функции.

В частном случае, когда переменные являются непрерывными и зависимость между ними линейная, уравнение может быть переписано в следующем виде:

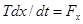                                                                                                                                     (6.5)

Здесь коэффициент пропорциональности Т имеет смысл постоянной времени, характеризующей инерционность переменной. Практически в нейросетях ее задают произвольно, руководствуясь желанием обеспечить, с одной стороны, достаточно высокую скорость, с другой- устойчивость процесса. В дискретном случае задание Т определяет величину шага процесса 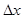, т.е. изменение переменной за один такт. Чем больше Т, тем меньше шаг и тем медленнее протекает процесс. Основное уравнение динамики в этом случае можно записать в виде:
 

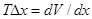
В случае с двоичными переменными этот шаг предопределен характером переменной: он либо равен 1 (если переменная принимает значения 0 и 1), либо 2 (если ее значение +1 и -1). В противном случае уравнение динамики может быть записано в виде:

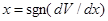
Все типы уравнений динамики и различные их комбанации используются в описании нейросетей.
Используем в качестве примера сеть Хопфилда [71].
Целевая функция может быть описана в виде:

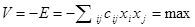
Переменные обычно являются двоичными, весовые коэффициенты сijмогут рассматриваться как дискретные или непрерывные переменные. Предположим, что значения всех переменных xi фиксированы, свободными переменными являются только веса межнейронных связей сij. Изменение этих переменных означает обучение сети. Основное уравнение динамики в этом случае выглядит так:
 

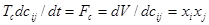
Если сij - дискретные переменные, то уравнение примет вид:

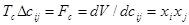
Это есть не что иное, как правило Хебба для формирования весовых коэффициентов в процессе обучения (с точностью до константы Тс).

Предположим теперь, что фиксированы значения весовых коэффициентов сij (сеть обучена) и некоторые из признаков хj(задана частичная информация об эталоне). Для оставшихся свободными признаков основное уравнение динамики принимает вид:

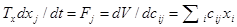
Здесь 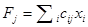и есть равнодействующая сил вида: 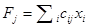, действующих на переменную  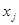со стороны переменных 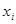, через связи .
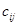Если 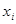- двоичные переменные, принимающие значения +1,-1, то формула превращается для них в выражение:

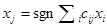
В таком виде это уравнение динамики первоначально и было написано Хопфилдом.