Сеть Хопфилда поддерживает множество лишних, неэффективных связей, по существу дублирующих друг друга. В реальных нервных системах поддержание таких связей требует определенных затрат и потому невыгодно. Поэтому в ходе эволюции нервной системы происходило освобождение от части связей за счет централизации системы связей. Подобная централизация является общесистемной закономерностью и наблюдается во многих системах- биологических, технических, социальных. Например, первые телефонные сети непосредственно связывали абонентов друг с другом. Однако с ростом числа абонентов число связей N росло приблизительно пропорционально квадрату числа абонентов n:
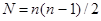
и сети быстро усложнялись. Тогда были введены центральные телефонные станции, так что каждый абонент теперь соединялся непосредственно только с телефонной станцией и уже через нее - с другими абонентами. Число связей резко уменьшилось:
N = n,
а с ними уменьшились и затраты на их поддержание.
Подобную эволюцию проделала и нервная система животных- от диффузной у простейших к центральной нервной системе и головному мозгу у высших млекопитающих. Поэтому связь многих элементов с одним, центральным следует считать более высоким принципом организации, чем связь "всех со всеми". Множество центральных элементов образует новый уровень или слой, для которого, в свою очередь, справедлив тот же принцип организации. Так возникает многослойная иерархическая система связей. Склонность к такой организации обнаруживают и системы обработки информации, как естественные, так и искусственные. Их можно найти уже в традиционных системах распознавания образов - в виде иерархической организации системы признаков, когда из простых признаков строятся более сложные, а из них уже - фрагменты образов и далее - сами образы.
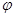В качестве примера такого подхода рассмотрим метод группового учета аргументов, предложенный А.Г. Ивахненко [72], или его аналог - метод ?-функций [73], основная идея которых состоит в следующем.
Любую нелинейную функцию n признаков xi,задающую желаемое отображение входного пространства в выходное, можно аппроксимировать с помощью полинома:
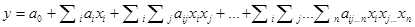
Коэффициенты полинома должны быть подобраны так, чтобы обеспечить желаемую зависимость у от х и распознавание с минимальной ошибкой. Для точного отыскания коэффициентов можно использовать систему нормальных уравнений Гаусса. Однако, при сколько-нибудь высокой степени полинома и при достаточном количестве признаков размеры матриц этой системы уравнений растут катастрофически. Так, при десяти признаках матрица содержит 2*105*2*105 элементов. Этот процесс проявляет себя и при использовании адаптивных методов отыскания коэффициентов полиномов: время обучения оказывается неприемлемо большим.
В математике давно уже найден выход из этой ситуации. Он состоит в использовании различных систем стандартных функций, таких, как полиномы Чебышева, Эрмита, гармонические функции и пр. Сущность подхода- в иерархической организации сложных зависимостей. Стандартные функции подбираются так, что они, с одной стороны, сами уже обладают достаточно сложными и интересными свойствами, с другой- их можно достаточно просто комбинировать для аппроксимации еще более сложных функций. Иными словами, полином строится не из простейших - степенных функций, а из более сложных. При этом оказывается, что невозможно предложить единую систему стандартных функций, пригодную на все случаи жизни, - для каждой области приложений наиболее подходящей оказывается своя система стандартных функций.
В методе группового учета аргументов сложный полином заменяется несколькими более простыми, учитывающими только некоторые признаки ("группы аргументов"). При этом каждый упрощенный полином рассматривается как самостоятельный независимый классификатор, коэффициенты которого определяются путем решения системы нормальных уравнений Гаусса малой размерности (т.е. точным методом). После обучения отбирается несколько наилучших (в смысле результатов классификации) полиномов, и их левые части yj("сложные признаки") используются в качестве аргументов для построения более сложного полинома. Практически использовались различные попарные объединения признаков, что давало возможность строить в качестве границ прямые и кривые второго порядка.
Таким образом, иерархическая организация признаков- общий путь, обеспечивающий компромисс между желаемой точностью и приемлемыми затратами на поиск или обучение. Возможность именно такой организации и предоставляет пользователю нейронная сеть с ее готовым набором стандартных нелинейных функций. Если раньше в качестве такого стандарта выступала пороговая зависимость, позволяющая проводить границы в пространстве признаков, то сейчас в качестве альтернативы применяются уже и другие стандартные наборы (потенциальные функции, радиальные базисные функции и пр.), оперирующие не с границами, а непосредственно с областями.
Необходимость иерархии во многом и определяет структуру большинства современных нейронных сетей. Важнейшим нововведением и главной отличительной особенностью этой структуры является наличие промежуточного слоя (или нескольких слоев) "скрытых нейронов". Скрытые элементы не являются узкоспециализированными, они не связаны жестко ни с входными образцами, ни с выходными реакциями, эта свобода и придает нейросети необыкновенную гибкость, вычислительную мощность и способность адаптироваться к самым разным комбинациям входов и выходов. Наличие скрытых элементов позволяет нейросети выполнять действия, сходные с теми операциями по преобразованию и сокращению исходных данных, которые давно уже используются в многомерной статистике. Вот некоторые очевидные аналоги функций, выполняемых скрытыми элементами:
- "главные компоненты" в факторном анализе;
- "координаты" в многомерном шкалировании;
- "дискриминантные функции" в дискриминантном анализе.
Сеть со скрытыми элементами может реорганизовать пространство входных признаков в простые области, затем объединить их в более сложные (невыпуклые, несвязные) и, наконец, ассоциировать их с выходными категориями.
Другими факторами, определяющими архитектуру нейросети, являются условия связи с внешней средой: сеть должна иметь число входных элементов, равное размерности пространства признаков; число выходных- размерности пространства ответов. Число промежуточных (скрытых) элементов определяется сложностью задачи, требуемым объемом памяти и допустимой ошибкой распознавания.
