Один из самых неожиданных результатов анализа И.Минского и С.Пейперта состоял в том, что персептрон, построенный на линейных функциях активации, не может воспроизвести такую простую логическую функцию, как исключающее ИЛИ (XOR). Это функция двух аргументов у(х1, х2) всего возможны четыре комбинации значений аргументов: 00, 01, 10, 11. В пространстве признаков они расположены по углам единичного квадрата (Рисунок 7.3 ). Функция у = (х, XOR х2) равна единице, когда равен единице один из аргументов, но не оба сразу. Таким образом, множество точек (01, 10) относится к классу, где у = 1, а множество (00, 11) - к классу у = 0. В пространстве признаков элементы этих классов лежат на противоположных углах квадрата и никакая линейная функция у(х1, х2) от этих признаков не способна разделить эти два класса. В этом случае не помогает и использование второго слоя нейронов, так как произведение двух линейных преобразований снова дает линейное преобразование, обладающее теми же недостатками. Выходом является использование нелинейных элементов.
Для иллюстрации этого вывода рассмотрим простой пример, когда пространство признаков является одномерным. Даже в этом случае легко построить задачу, которая не может быть решена с использованием только линейных функций активации.
Пусть в одномерном пространстве признаков х\ элементы одного класса (нулики) расположены вокруг элементов другого класса (крестиков) (Рисунок 7.4 ), т.е. множество нуликов является несвязным. Необходимо построить такую функцию f(x\), которая принимала бы положительное значение на крестиках и отрицательное - на нуликах. Это позволит разделить все пространство х на три области и затем крайние области (отрицательные значения f(x1)) объединить в один класс, а среднюю (положительные значения а) отнести к другому. Желаемая (идеальная) зависимость у'(х), решающая эту задачу -Рисунок 7.4 , а. Как видно из рисунка, она является нелинейной: нужна кривая по меньшей мере второго порядка,
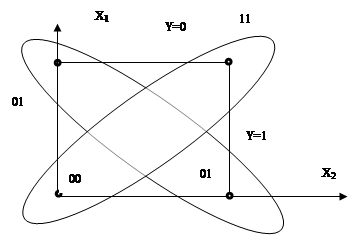
Рисунок 7.3 Пространство признаков для функции у=х1 xor х2
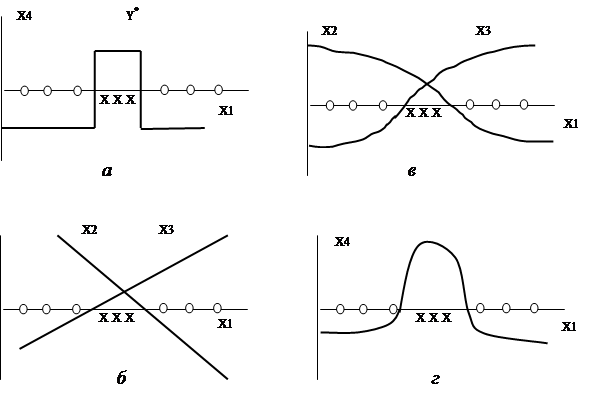
Рисунок 7.4 Использование нелинейных функций активации:
а - идеальная зависимость; б - линейные зависимости;
в - сигмоидальные зависимости; г - решение задачи с помощью нейронной сети с сигмоидальными зависимостями, чтобы она пересекла ось x дважды и разделила ее на три части. Из рисунка 6.4, б следует, что никакие линейные зависимости или их комбинации (в одномерном пространстве это просто прямые) не позволяют решить эту задачу: любая комбинация прямых дает снова прямую, а она пересекает ось х только в одной точке и делит все пространство х только на две области. Иное дело - нелинейные, например ступенчатые или сигмоидальные, функции (Рисунок 7.4 ,в).
Для реализации требуемой зависимости необходима сеть, состоящая из пяти нейронов (Рисунок 7.2 ). Нейрон х1 является рецептором, он воспринимает значение "признак х1 “и просто транслирует его дальше. Нейрон х0 является "псевдонейроном"- его задача создавать постоянный сигнал +1, который, умноженный на веса c0i, формирует пороговые значения для других нейронов. Нейроны х2 и х3 -основные рабочие нейроны сети. Их активационными функциями являются сигмоиды (Рисунок 7.4 , в). Наклон характеристики - положительный для хз или отрицательный для x3 - задается весовыми коэффициентами c13 и c12, а положение на оси х - порогами c03 и c02 соответственно:
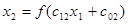
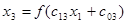
Наконец, выходной нейрон x4 просто суммирует эти сигмоиды - с какими-то порогами и весами:
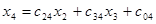
В результате получается зависимость выхода сети x4 от входа x1,решающая задачу разделения крестиков и нуликов: она положительна для крестиков и отрицательна для нуликов (Рисунок 7.4 , г).
Одна из тенденций в развитии нейронных сетей состоит в переходе к более гибким и универсальным нелинейным функциям. Суть тенденции может быть понята из следующего рассуждения: целью обучения обычно является выделение областей, занимаемых различными классами. Средством же является проведение границ, поскольку пороговый элемент- линейный или нелинейный- определяет именно границу в пространстве признаков. И только на следующем уровне иерархии с помощью границ выделяются области. Такой путь неудобен, особенно если область, занимаемая классом, имеет сложную форму, является многосвязной (как в случае исключающего ИЛИ). По-видимому, будет лучше (по крайней мере в некоторых случаях), если с элементом связывается не граница, а сразу некоторая стандартная элементарная область, которая может служить базисом для построения более сложных областей. Например, можно описывать нейрон ступенчатой активационной функцией у(х), положительной в некоторой области пространства признаков и отрицательной- во всех остальных областях этого пространства (Рисунок 7.4 , а). Настраиваемыми параметрами при этом могут быть размеры области и ее положение в пространстве признаков. Тогда задачу о разделении крестиков и нуликов можно было решить с помощью единственного нейрона. Суммируя выходы нескольких таких нейронов, можно легко выделить область самой сложной формы. Ступенчатую функцию при этом можно, конечно, сгладить (например, как на Рисунок 7.4 , г), чтобы иметь возможность использовать градиентные методы поиска экстремума.
Из классических методов распознавания наиболее близок к этому известный метод потенциальных функций. Сейчас используют нейросети именно такого рода функции (радиальные базисные функции, p-функции и т.п.). Так, сферическая радиальная базисная функция i-го нейрона может задаваться выражением, аналогичным выражению для нормального распределения. Комбинация элементов такого или подобного типа способна аппроксимировать любую нелинейную зависимость и, следовательно, выделить в пространстве признаков области самой сложной формы- невыпуклые, многосвязные и т.п.
В целом архитектура нейросети может быть задана матрицей весовых коэффициентов cij характеризующих силу связей между элементами сети. В общем случае все элементы связаны со всеми, но матрица связей несимметрична, cij не равно cji. Некоторые коэффициенты связей могут оставаться свободными, незаданными и тогда возможно их изменение- обучение сети.
Таким образом, налагая условия на значения cij, предопределяется конфигурация сети. При этом из множества возможных конфигураций получили распространение и достаточно хорошо исследованы лишь некоторые. К числу важнейших относятся две конфигурации:
- однослойная сеть Хопфилда;
- трехслойная сеть с промежуточным слоем "скрытых" нейронов.


