С конструктивной точки зрения нейрон, являющийся основным элементом нейросети, - это устройство для получения нелинейной функции нескольких переменных Xi свозможностью настройки его параметров Cjв достаточно широком диапазоне. Однако традиционно нейрон описывается в терминах, заимствованных из физиологии. Согласно этим представлениям нейрон имеет один выход Sjи несколько входов (синапсов), на которые поступают внешние воздействия Xj, (от рецепторов и других нейронов). Он умножает входное воздействие на весовой коэффициент Cij(проводимость синапса) и суммирует взвешенные входы:
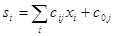 (6.1)
(6.1)
Выходная величина yiявляется некоторой функцией от этой суммы:yi=f(Sj). Ее называют функцией активации или передаточной функцией. Вид этой функции является важнейшей характеристикой нейрона. В простейшем случае - это линейная зависимость (Рисунок 7.1 , а).
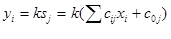
Такая зависимость использовалась в первых моделях персептрона. Несмотря на ряд первоначальных успехов, теоретический анализ возможностей персептрона, проведенный М.Минским и С.Пейпертом [68], показал, что персептрон не является универсальным устройством для распознавания и, в частности, принципиально неспособен решить целый ряд весьма простых задач. Причиной этого является именно линейный характер активационной функции.
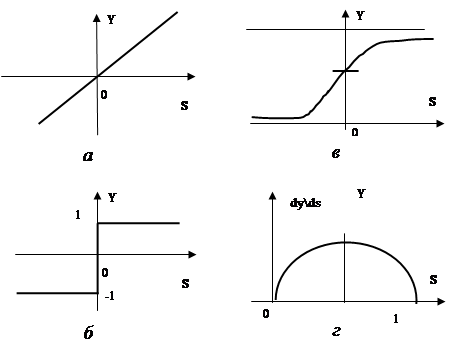
Рисунок 7.1 Функции активации нейронной сети: а – линейная функция;
б- ступенчатая функция; в- сигмоидальная функция;
г- производная от сигмоидальной функции
Еще использовалась ступенчатая функция активации: если сумма Sjвыше некоторого порогового значения c0j, то выход yjравен единице, в противном случае- минус единице (или нулю). Формально это можно описать с помощью следующей зависимости (Рисунок 7.1 ,6):
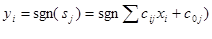
В настоящее время в качестве активационной функции чаще используют близкую к ступенчатой, но более гладкую зависимость, которую называют сигмоидальной, или логистической, функцией (Рисунок 7.1 , в). Обычно она описывается следующим выражением:
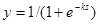
Встречаются и другие выражения, например,
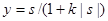 ,
,
где |s| - абсолютная величина s, k> 0.
Параметр kзадает крутизну зависимости у от s: чем больше k, тем ближе сигмоида к пороговой функции; чем меньше k, тем ближе она к линейной. Таким образом, сигмоида является некоторым компромиссом между линейной и ступенчатой функцией, сохраняющим достоинства обеих. Подобно ступенчатой функции, она нелинейная, и это важно, поскольку только нелинейные функции позволяют вычленять в пространстве признаков множества сложной формы, в том числе невыпуклые и несвязные. Но в то же время сигмоида в отличие от ступенчатой функции переходит от одного значения к другому без разрыва, как это имеет место и в линейной функции. Это обстоятельство оказывается чрезвычайно важным при поиске экстремума целевой функции в пространстве нейронных параметров, в этом случае зависимость целевой функции от параметров также оказывается гладкой, и в каждой точке пространства может быть вычислен градиент целевой функции, указывающий направление поиска экстремума.
Производная от сигмоидальной функции, характеризующая силу связи между sи у, также имеет простой вид:
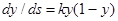 (6.2)
(6.2)
Эта величина обращается в нуль на границах диапазона изменения у при y=0 и у=1 и достигает максимума в середине диапазона, т. е. связь между переменными наиболее сильна в середине диапазона и ослабевает к его краям (Рисунок 7.1 , г).
Нейроны организуются в сеть (Рисунок 7.2 ) за счет того, что выход i-roнейрона (уi) соединяется с одним из входов (хi) другого j-го нейрона. При этом выходная переменная ytотождествляется с входной переменной хi. Поэтому в дальнейшем будем использовать оба обозначения в зависимости от того, рассматривается ли данная i-я переменная как входная или как выходная. Весовой коэффициент сij("синаптический вес") характеризует знак и силу связи между переменными хi и yi. Возможна и обратная связь, при которой выходу j-го нейрона соединяется с j-м входом j-го нейрона. В общем случае коэффициент связи сij, не обязательно равен сji.
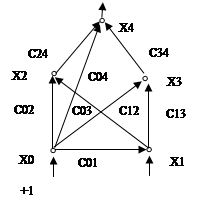
Рисунок 7.2 Пример нейронной сети
Важнейшим свойством нейрона является его пластичность - возможность изменять параметры в процессе обучения:. В ранних работах по нейросетям обычно различали два типа пластичности:синаптиче-скую (изменение сij) и нейронную (изменение высотгы порога нейрона с0j) В настоящее время пороговую пластичности, обычно сводят к синаптической с помощью следующего приема. К числу входов j-го нейрона добавляют еще один фиктивный x0, не связанный ни с каким реальным рецептором (Рисунок 7.2 ). На этот вход подают постоянный сигнал, равный +1. Весовой коэффициент этого входа с0jмодифицируют в процессе обучения по общим правилам. Модификация этого коэффициента равносильна смещению порога нейрона.
Еще в 1949 г. Д. Хеббом [19] было предложено естественное правило модификации весовых коэффициентов: если два нейрона возбуждаются вместе, то сила связи между ними возрастает; если они возбуждаются порознь, то сила связи между ними уменьшается. Правило оказалось настолько удачным, что до сих пор используется в различных моделях нейронных систем. Формальнее это правило может быть описано следующим образом. Пусть время обучения разбито на такты и в k- м такте две переменные нейросети (состояния двух нейронов) имели значения xki , и xkj. Тогда вес связи между переменными возрастает на величину
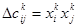
В случае двоичных переменных приращение равно либо +1 (при совпадении знаков xki и xkj ), либо -1 (когда знаки различны). Если начальный вес связи был равен нулю, то вес связи к k-му такту равен:
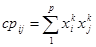
где xki, xkj - состояния двух нейронов в k-м такте; р - число тактов обучения.


