Рассмотрим пример, иллюстрирующий распространение коэффициентов определенности в сети (Рисунок 6.8 ).
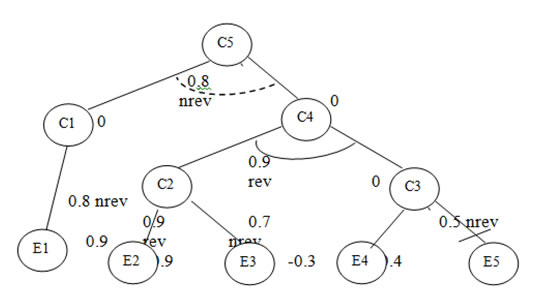
Рисунок 6.8 Пример сети вывода для проведения рассуждении с заданными начальными условиями
Узлы в основании дерева представляют условия из внешнего мира, о которых система должна задавать вопросы. Внутренние узлы отображают заключения. Коэффициенты определенности внутренних узлов полностью зависят от процесса рассуждения, правил импликации и свидетельств, полученных из внешнего мира путем запросов. Число справа от каждого узла соответствует коэффициенту определенности. До начала рассуждений ничего не известно о внутренних узлах, поэтому они все имеют коэффициенты определенности, равные нулю.
Рядом с коэффициентом определенности импликации rev (обратимо) или nrev (необратимо), что обозначает, будет ли импликация использоваться как обратимое или как необратимое правило. Вычисление коэффициента определенности посылки может потребовать выполнения нескольких шагов: могут добавляться "И", "ИЛИ", "НЕ". В каждом конкретном случае, пока не будет закончена вся эта предварительная работа, нельзя с уверенностью сказать, применимо ли правило.
Сеть вывода (Рисунок 6.8 ) предполагает следующие правила:
Если (е1), то (с1) сt = .8 (nrev)
Если (е2), то (с2) сt = .9 (rev)
Если (еЗ), то (с2) сt = .7 (rev)
Если (е4), то (сЗ) сt = .6 (nrev)
Если (не е5), то (сЗ) ct = .5 (nrev)
Если (с2 и сЗ), то (с1) сt = .9 (rev)
Если (с1 или с4), то (с5) ct = .8 (nrev)
Ниже (Рисунок 6.9 ) показан результат всех рассуждении, проводимых в сети, использующей подходящее свидетельство.
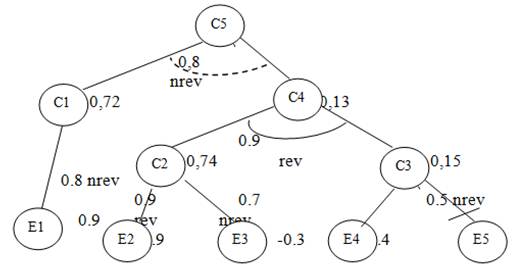
Рисунок 6.9 Пример сети вывода с вычисленными коэффициентами
Коэффициент определенности С1 может быть вычислен следующим образом:
сt(заключение с1) = .8 * .9 = .72.
Это простая необратимая импликация, но поскольку коэффициент определенности посылки позитивен, правило можно применять.
При вычисления коэффициента определенности С2 оба правила используются без ограничений, так как они обратимы. Правило слева даст оценку коэффициента определенности С2:
сt(заключение C2) = .9 * .9 = .81.
Правило справа даст иную оценку:
сt(заключение C2) = -.3 * .7 = -.21.
Здесь два поддерживающих правила, дающих оценку коэффициента определенности с противоположными знаками, поэтому для окончательного ответа объединим эти оценки:
сt(заключение С2) = (.81+ (-.21))/(1 —.21) = .74.
Для C3 опять два правила. Правило, связанное с левым поддеревом, не применяется, так- как оно необратимо, и коэффициент определенности посылки отрицателен. Правило, связанное с правым поддеревом, есть простая импликация. Она необратима и содержит отрицательную посылку. Правило утверждает:
Если (не E5) то (CЗ) ct = .5 (nrev)
Коэффициент определенности E5 равен -.3. Так как он негативен, то коэффициент определенности посылки в правиле равен .3. Правило необратимо, но посылка находится в допустимом интервале. Используя процедуру, предназначенную для простой импликации, найдем для CЗ:
сt(заключение СЗ) = .3 * .5 = .15.
Импликация, поддерживающая С4, включает конъюнкцию посылок. Коэффициент определенности посылки равен:
сt (свидетельства) = min(.15, .74) =.15.
Поскольку правило обратимо, можно использовать посылку в любом интервале определенности. Используя этот результат, вычислим коэффициент определенности для C4:
ct (заключение C4) =.15* .9 =.13.
Теперь прошли вверх по дереву до того места, где можно судить об узле верхнего уровня. Здесь задействовано одно правило, в котором посылки разделены с помощью ИЛИ, поэтому:
сt (свидетельства) = mах (.72, .13) = .72.
Правило необратимо, но коэффициент определенности посылки позитивен, так что можем двигаться дальше.
Последнее звено в нашей цепи рассуждении - коэффициент определенности для узла высшего уровня - вычисляется по формуле:
ct (заключение с5) = .72 * .8 =.58.
Обычно сети вывода требуются в ситуации, когда при наличии нескольких конкурирующих гипотез экспертная система пытается сделать выбор и породить информацию. Например, в медицинских системах сеть выбора может использоваться при установлении причин болей у пациента: аппендицит ли это, рак, какая-нибудь инфекция, вызвавшая воспаление лимфатических узлов, или, возможно, просто расстройство желудка.
Программа иллюстрирует хороший способ представления связей и импликаций в типичной сети вывода. Кроме того, для всех узлов, названных здесь конкурирующими гипотезами, программа может получать информацию целесообразным образом и рассуждать, чтобы сделать выбор между гипотезами верхнего уровня на основе вычисленных определенностей.
Все правила обратимы. Они могут быть использованы для всех возможных значений коэффициента определенности посылки.
Связи между узлами представляют основные шаги рассуждений. Включаем их в программу с помощью фактов импликации. Например, в с1 расположен узел И. Его структура в форме правила выглядит так:
Если ((не е1) и е2), то (cl) ct = .9 (rev)
Предикат на языке Prolog может быть таким:
imp(a, r, c1, neg, el , pos, e2, 0.9).
где а – тип связи И (AND) или о – ИЛИ (OR) или s – простая связь; r – правило обратимо (rev); с1 – имя узла; neg (или pos ) - перед каждым узлом указывает шаблон отрицания в правиле, если таковой имеется. Коэффициент определенности данной конкретной импликации равен .9.
Все остальные понятные программе импликации можно представить с помощью тех же восьми аргументов фактов импликации. Простая импликация представляется так:
lmp(s,r,c3,pos,e5, dummy, dummy,0.6).
Здесь записано, что узел сЗ поддерживается указанной импликацией, а е5 - посылка. Посылка не отрицается, поэтому правило обратимо. Аргументы 6 и 7 (dummy,dummy) будут всегда присутствовать в простых импликациях, так что можно использовать одну и ту же форму для представления всех импликаций, о которых известно программе.


