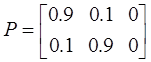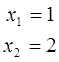Нечеткие множества и нечеткая логика

Для формализации нечетких знаний, характеризуемых лингвистической неопределенностью, применяется теория нечетких или расплывчатых множеств. Основы теории нечетких множеств были созданы в 1965 году Л.А. Заде (США).

Пусть имеется множество Х и его собственное множество А, т.е. А ? Х. Тогда подмножество А можно представить в виде совокупности упорядоченных пар:

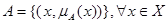
где mA(x) функция принадлежности. Причем:

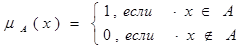
Рассмотрим в качестве примера [64] множество, представляющее возможные значения температуры воздуха. Тогда введение функции принадлежности, условно изображенной на Рисунок 6.3 сплошной линией, позволит выделить подмножество отрицательных температур, а изображенной пунктирной линией- подмножество положительных температур. При этом нулевая температура относится ко второму подмножеству.

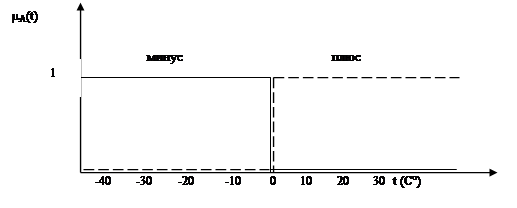
Рисунок 6.3 Функция принадлежности для четкого множества

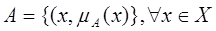Приведенное определение подмножества A и пример функции принадлежности, принимающей всего два возможных значения 0 и 1, соответствует четкому (обычному) подмножеству. Определение нечеткого подмножества получается как обобщение этого определения. Нечетким подмножеством А множества Х будем называть совокупность упорядоченных пар:

где функция принадлежности mA(x) каждому элементу х ставит в соответствие действительное число из интервала [0, 1], указывающее степень принадлежности элемента х подмножеству А.

Математическая структура, определяемая выражением

А = {(х1 |0,8) , (х2 |0,3), (х3 |0), (х4 |0,5 )},

где х1, х2, х3, х4 - элементы универсального множества X, представляют собой пример нечеткого подмножества. Здесь степени принадлежности элементов х1, х2, х3, х4 подмножеству А заданы числами после вертикальной черты. Наивысшую степень принадлежности имеет элемент х1. Элемент х3 подмножеству А не принадлежит. Элементы х2 и х4 принадлежат А в меньшей степени, чем х1 . Таким образом, используя понятие нечеткого подмножества, можно представлять объекты (сущности) предметной области, характеризуемые размытыми границами описаний.

Нечеткое множество А называется нормальным, если

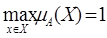
Если это свойство не выполняется, то А называется субнормальным. Непустое подмножество А всегда можно нормализовать делением на максимальное значение функции принадлежности. Носителем нечеткого подмножества А называется подмножество элементов Х, для которых mA(x) > 0. Переменная x называется базовой.

При практическом применении нечетких множеств важным являются понятия нечеткой и лингвистической переменной [54]. Лингвистическая переменная (ЛП) – это переменная, значение которой определяется набором вербальных характеристик некоторого свойства. Например «рост» определяется через набор {карликовый, низкий, средний, высокий, очень высокий}.

Приведем пример из [54] интерпретации значений ЛП «возраст», который может быть определен через набор {младенческий, детский, юный, молодой, зрелый, старый}. Для ЛП «возраст» базовая шкала от 0 до 120 лет, обозначающая количество прожитых лет, а функция принадлежности определяет, насколько мы уверены в том, что данное количество лет можно отнести к данной категории возраста. Рисунок 6.4 показывает, как одни и те же значения базовой шкалы могут участвовать в определении различных нечетких множеств.

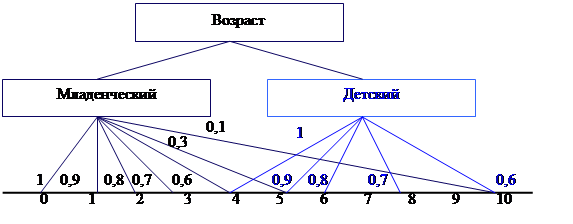
Рисунок 6.4 Формирование нечетких множеств

Определим значение нечеткого множества «младенческий возраст»:

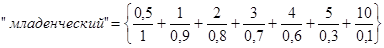
Основные операции с нечеткими множествами

Обозначим через А и В нечеткие подмножества множества Х.

Тогда нечеткие множества А и В равны, если:

А=В, если

Множество А содержится в В, если:

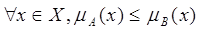
Нечеткие множества А и В дополняют друг друга, если:

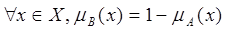
Множество с функцией принадлежности 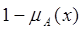есть дополнение к множеству А (обозначается ).

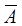Пересечение двух нечетких множеств А и В (обозначается ):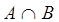

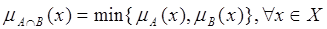
Объединение двух нечетких множеств А и В (обозначается ):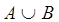

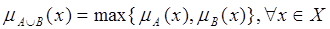
Операции пересечения и объединения нечетких множеств ассоциативны и дистрибутивны.

Алгебраическое произведение нечетких множеств А и В (обозначается 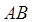)есть нечеткое множество, для которого

Алгебраическая сумма нечетких множеств А и В (обозначается )есть нечеткое множество с функцией принадлежности

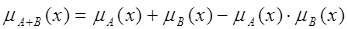
Дизъюнктивная сумма нечетких множеств А и В определяется через операции объединения и пересечения

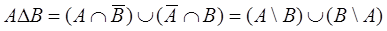где выражения и 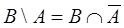представляют соответствующие разности множеств А и В. В общем случае .

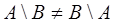Важным понятием теории нечетких множеств является нечеткое отношение. Нечетким бинарным отношением 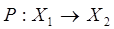называется подмножество декартового произведения двух множеств 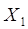и :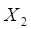

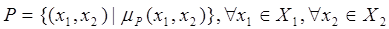где 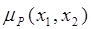- функция принадлежности пары элементов (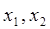) к P.

В общем случае n – арное отношение Pопределяется на прямом произведении множеств 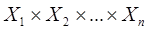с помощью формулы

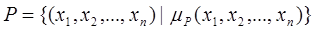где 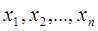элементы множества .

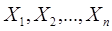Пусть множества X и Yсостоят из элементов X={1.2}, Y={1.2,2.1,5}.Зададим нечеткое нечеткое бинарное множество в виде матрицы, элементами которой будут значения :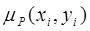

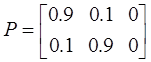
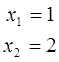
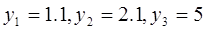
В частности, данная матрица может представлять нечеткое отношение “X примерно равно Y“.

Часто нечеткие отношения используются для представления правил типа если А то В , где А и В нечеткие подмножества (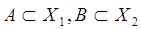). Такое правило обозначает . Один из способов задания нечеткого множества состоит в использовании формулы декартового произведения множеств А и В (обозначаемого ):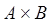

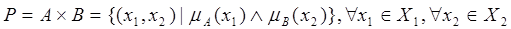Здесь

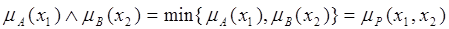причем 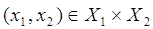.