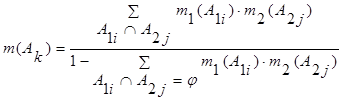Подход, принятый в теории Демпстера-Шефера (ТДШ) [64] отличается от байесовского подхода и метода коэффициентов уверенности тем, что, во-первых, здесь используется не точечная оценка уверенности (коэффициент уверенности), а интервальная оценка. Такая оценка характеризуется нижней и верхней границей, что более надежно. Во-вторых, ТДШ позволяет исключить взаимосвязь между неопределенностью (неполнотой знаний) и недоверием, которая свойственна байесовскому подходу.
В рамках ТДШ множеству высказываний А приписывается диапазон значений [Bl(А),Р1(А)], в котором находятся степени доверия (правдоподобия) каждого из высказываний. Здесь В1(А) - степень доверия к множеству высказываний, изменяющая свои значения от 0 (нет свидетельствв пользу А)до 1 (множество высказываний А истинно); Р1(А) - степень правдоподобия множества высказываний А, определяемая с помощью формулы: Pl(A) = 1-Bl(not A)
Предположим, что существуют две конкурирующие гипотезы h1 и h2. При отсутствии информации, поддерживающей эти гипотезы, мера доверия и правдоподобия каждой их них принадлежат отрезку [0; 1]. По мере накопления эти интервалы будут уменьшатся, а доверие гипотезам – увеличиваться. В теории Демпстера-Шефера неопределенность знаний представляется с помощью некоторого множества X. Элементы этого множества соответствуют возможным фактам или заключениям. Неопределенность состоит в том, что заранее неизвестно, какое из возможных значений примет факт или заключение х ? X. Для характеристики степени определенности в ТДШ вводится некоторая единичная мера уверенности (ее называют также единичной массой уверенности), которая распределяется между элементами X. При этом, если вся масса (степень) уверенности приходится на один элемент х ? X, то никакой неопределенности нет. Неопределенность возникает, когда масса уверенности распределяется между несколькими элементами х ? X. Распределение масс уверенности (Рисунок 6.2 ) между элементами множества X, представлено в виде точек [64].Здесь Х={х1 , х2 , х3}.
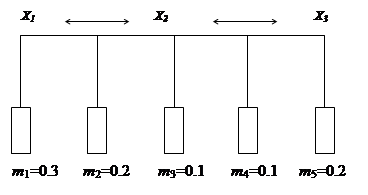
Рисунок 6.2 Распределение масс уверенности
С каждым элементом множества X жестко связана соответствующая масса уверенности. Так, х1 соответствует m1= 0,3 x2-m2= 0,1 x3-m3= 0,2. Имеются также свободные массы уверенности m4= 0,2 m5= 0,2, которые относятся сразу к нескольким элементам. Масса m4 свободно перемещается между элементами x1 и x2, а масса m5 - между элементами x2 и x3, т.е. m4 закреплена за подмножеством {x1, x2}, а m5 - за подмножеством {x2, x3, }. Массы выражают степень уверенности в возможных значениях фактов или заключений. Так, степень уверенности в значении х1 может изменяться от 0,3 до 0,5. Таким образом, степень незнания соответствует массе, местоположение которой не определено.
В общем случае распределение масс уверенности задается функцией m(А), обладающей следующими свойствами:
m(?)=0,
?m(А)=1,
Здесь А - множество, образованное из подмножеств X, которым назначены соответствующие массы (степени) уверенности; m(А)- функция, которая задает отображение А на интервал [0, 1]. Для примера (Рисунок 6.2 ) имеем:
А = {?, {х1}, {х2}, {х3}, {х1,х2}, {х2,х3}, {х1,х3}},
а распределение масс уверенности задаётся функцией m(А), характеризуемой множеством значений:
т(А) = {0; 0,3; 0,1; 0,2; 0,2; 0,2; 0}.
Обратим внимание, что А состоит из подмножеств. Обозначим каждое такое подмножество через Аi. Степень доверия к высказываниям, соответствующим подмножеству Аi, может быть вычислена по формуле
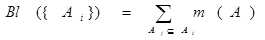

Здесь суммирование выполняется по всем остальным подмножествам Aj входящим A1 . Например:
Bl({х1,х2}) = m(A1)+m(A2)+m(A3)=m({x1})+m({x2})+m({x1, x2})=
0.3+0.1+0.2=0.6
Результаты вычислений степеней правдоподобия даны ниже (Таблица 6.2 ).
Таблица 6.2 Значения Bl(Ai) и Pl(Ai)
|
Ai |
? |
{х1} |
{х2} |
{х3} |
{х1,х2} |
{х2,х3} |
{х1,х3} |
X |
Bl(Ai) |
0 |
0.3 |
0.1 |
0.2 |
0.6 |
0.5 |
0.5 |
1 |
Pl(Ai) |
0 |
0.5 |
0.5 |
0.4 |
0.8 |
0.7 |
0.9 |
1 |
Степень правдоподобия подмножества Аi определяется по формуле:
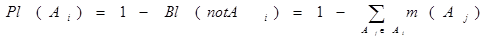
Величины Bl(Ai) и Pl(Ai) имеют простую интерпретацию: Bl(Ai) представляет общую массу уверенности, которая остается, если из X удалить все элементы, не ассоциируемые с Ai. Pl(Ai) представляет максимальную массу уверенности, которую можно получить, если сдвинуть свободные массы к элементам множества Ai. Причем Bl(Ai) ?Pl(Ai) . Иными словами, Bl(Ai) представляет нижнюю границу доверия к Ai, а Pl(Ai) - верхнюю.
Важнейшим элементом ТДШ является правило комбинации свидетельств:
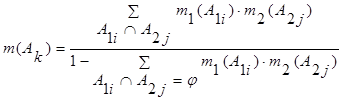
Сумма в числителе правила распространяется на множество Ak = A1i ? A2j. Правило является эвристическим и позволяет осуществлять распределение степеней доверия в ходе вывода. Например, мерой доверия mn(Z) гипотезе Z – для n=3 источников свидетельств считается сумма произведений гипотетических мер доверия m1(X) и m2(Y), совместное вхождение которых поддерживает Z, т.е. X ? Y =Z. Знаменатель в правиле Демстера допускает пустое пересечение X Y, а сумма мер доверия должна быть нормализована.
Рассмотрим применение правила Демпстера для задачи медицинской диагностики, описанное в [76].
Предположим, что рассматривается область Q, содержащая четыре гипотезы:
- пациент был без сознания (С);
- у него был грипп (F);
- мигрень (H);
- менингит (М).
Необходимо связать меры доверия со множествами гипотез в рамках Q. Например, лихорадка свидетельствеут в пользу {C,F,M}. Так как елементы Q трактуется как взаимоисключающие гипотезы, подтверджение одной из них может влиять на достоверность других.
Пусть есть свидетельство, что у пациента лихорадка. Оно поддерживает {C,F,M} с вероятностью 0,6. Назовем это первой мерой доверия m1. Если это всего лишь гипотеза, то m1{C,F,M}=0,6 , где m1{Q}=0,4 остаток (1-0.6) оставшуюся часть распределения достоверности, т.е. все другие возможные меры доверия Q, а не достоверность дополнения {C,F,M}.
Затем были получен факт о новом проявлении болезни- у пациента рвота, которая свидетельствует о {С,F,Н} со степенью доверия 0,7. Пусть это будет мера доверия свидетельства m2. Тогда имеем m2{C,F,Н}=0,7 , где m2{Q}=0,3.
Получаем таким образом множество X – набор подмножеств Q на котором m1 принимает ненулевые значения, и Y - набор подмножеств Q на котором m2 принимает ненулевые значения.
Применим правило Демпстера [76] для определения объединенной меры доверия m3: перемножим X и Y. Знаменатель равен 1, т.к. пока не существует пустых множеств X ? Y. Результат вычислений Таблица 6.3.
Таблица 6.3 Применение правила Демстера для объединения свидетельств m1 и m2
|
m1 |
m2 |
m3 |
m1{C,F,M}=0,6 |
m2{C,F,Н}=0,7 |
m2{C,F}=0,42 |
m1{Q}=0,4 |
m2{C,F,Н}=0,7 |
m2{C,F,H}=0,28 |
m1{C,F,M}=0,6 |
m2{Q}=0,3 |
m2{C,F,M}=0,18 |
m1{Q}=0,4 |
m2{Q}=0,3 |
m3{Q}=0,12 |
Обратите внимание на рассуждения и группировки гипотез. Четыре множества столбца m3 представляют собой все возможные пересечения X и Y. Этих данных явно недостаточно для установки диагноза, что и отражают полученные числа.
Добавим данные лабораторного анализа, который свидетельствует в пользу менингита m4{M}=0,8 и m4{Q}=0,2.
Применим еще раз правило Демпстера [76] для определения объединенной меры доверия m5. Результат вычислений Таблица 6.4.
Так как m5{M} получается в нескольких случаях, то общая вероятность m5{M}=(0,144+0,096)=0,240.
В результате пересечения нескольких пар множеств получается пустое множество {}, значит знаменатель в уравнение Демпстера нужно считать как
(1-(0,336+0,224))=0,44.
Таблица 6.4 Применение правила Демстера для объединения свидетельств m3 и m4
|
m3 |
m4 |
m5 |
m2{C,F}=0,42 |
m4{M}=0,8 |
m5{}=0,336 |
m3{Q}=0,12 |
m4{M}=0,8 |
m5{M}=0,096 |
m2{C,F}=0,42 |
m4{Q}=0,2 |
m5{C,F}=0,084 |
m3{Q}=0,12 |
m4{Q}=0,2 |
m5{Q}=0,024 |
m2{C,F,H}=0,28 |
m4{M}=0,8 |
m5{}=0,224 |
m2{C,F,M}=0,18 |
m4{M}=0,8 |
m5{M}=0,144 |
m2{C,F,H}=0,28 |
m4{Q}=0,2 |
m5{C,F,H}=0,056 |
m2{C,F,M}=0,18 |
m4{Q}=0,2 |
m5{C,F,M}=0,036 |
Окончательные значения меры доверия имеют вид:
|
m5{M}=0,240/0.44=0.545 |
m5{C,F}=0.084/0.44=0.191 |
m5{C,F,H}=0.056/0.44=0.127 |
m5{C,F,M}=0,82 |
m5{}=0,336+0.224=0.56 |
m5{Q}=0,024/0.44=0.055 |
Высокая достоверность пустого множества m5{}=0.56 означает существование конфликта свидетельств на множестве мер доверия mj т.к. в примере даны некорректные с точки зрения медицины данные.
При существовании больших множеств гипотез вычисление мер доверия может оказаться громоздким, но все же значительно меньше чем при использовании теоремы Байеса (раздел 6.2).
Правило Демстера- пример рассуждений субъективных вероятностей, в отличие от объективных вероятностей Байеса.