Подход “поиск в пространстве состояний” сформировался в результате попыток автоматизации игр. В большинстве игр имеется конечное число позиций (или “состояний”), которые могут быть достигнуты при использовании фиксированного набора правил, определяющих игру. Поэтому (по крайней мере, в теории) существует возможность описания последовательности игры путем перечисления всех позиций, которые могут быть достигнуты из заданного начального состояния. Это множество позиций может быть представлено в виде дерева, простирающегося от корня, который соответствует начальному состоянию игры, к заключительным позициям, достигаемым в конце игры.
Приведем все возможные позиции (Рисунок 4.5) для четырех первых ходов в простой игре “крестики-нолики”.
В рамках описанного выше представления “пространства состояний” положения фишек (состояния), соответствующие успешной игре, можно рассмотреть среди заключительных позиций дерева. Выигрышные последовательности ходов могут быть выявлены в результате прокладки пути от исходного состояния до выигрышного.
В игре “крестики-нолики” существует только один тривиальный оператор — установка фишки (0 или X) в пустой квадрат матрицы. Однако в других играх операторов может быть несколько. Например, в шахматах предписанные для каждой из фигур ходы можно рассматривать как операторы,
преобразующие картину шахматной позиции и таким образом продвигающие игру от одного состояния к другому.
Когда такие диаграммы применяются в системах, построенных на основе знаний, их обычно изображают по-другому: цель помешают наверху, а исходную позицию — внизу. Например, при обратном направлении поиска движение происходит от цели к начальному состоянию, а при прямом — от начального состояния к цели.
С достижением цели посредством полного перебора, в пространстве состояний связана достаточно серьезная проблема. Даже в такой простой игре, как “крестики-нолики”, существует 362880 (9!) возможных позиций. Благодаря симметрии некоторых из них эту цифру можно сократить приблизительно до 60 000. В таких сложных играх, как шахматы, было бы невозможно произвести поиск по всему дереву игры, так как просмотр вперед на 5 ходов дает квадриллион (1015) комбинаций, а 40 ходов (в среднем за игру) дают 10120 комбинаций. При этом с момента зарождения Вселенной прошло менее 1080 секунд! На каждом шаге количество вариантов выбора умножает общее число комбинаций. Этот процесс, получивший название “комбинаторного взрыва”, исключает применение стратегии поиска полным перебором для большинства реальных игр, а также и для большинства систем, на основе знаний. Ни один игрок не проводит поиск очередного хода простым перебором, а применяет определенные стратегические правила для выявления того, какие из ходов обеспечивают наибольшую возможность успеха. Во многих случаях это приводит к значительному сокращению числа просматриваемых позиций. В большинстве игр (и вообще ситуаций при обработке знаний) часто невозможно найти правила, гарантирующие успех. Вместе с тем нередко удается установить правила, обеспечивающие увеличение вероятности успеха. Такие правила называют эвристическими, а поиск, при проведении которого они применяются, называется эвристическим поиском.

Рисунок 4.5 Четыре хода в игре “крестики- нолики”
Для эвристического правила требуется информация о его эффективности. Эта информация определяется по некоторой “оценочной функции”. В игре “крестики-нолики” используется простая оценочная функция. Некоторое значение (число) присваивается каждому следующему возможному ходу. Чем оно выше, тем лучше для одного игрока и хуже для другого.
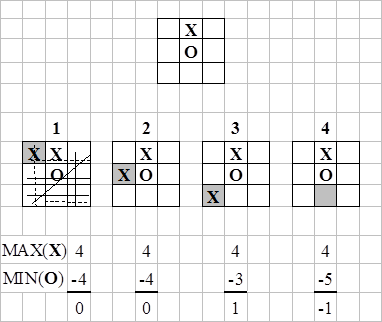
Рисунок 4.6 Применение эвристической оценочной функции
Эта процедура называется MINIMAX. Проиллюстрируем применение процедуры MINIMAX при игре в “крестики-нолики”
Допустим, что есть два игрока- MAX (играющий фишками X) и MIN (играющий фишками 0). Значение оценки для доступных им ходов могут быть получены путем подсчета всех линий, открытых для каждого из игроков, а затем вычитания одного числа из другого.
Применительно к позиции (Рисунок 4.6) , МАХ должен сделать выбор среди ходов 1, 2, 3 и 4. Они соответственно получают оценки 0, 0, 1, -1. МАХ выбирает ход 3, так как он получил наивысшую оценку для этого раунда.
В игре в “крестики-нолики” приемлема конструкция единственной оценочной функции, которая надежно прокладывает путь к оптимальному решению.
Другая стратегия [21] применяется в игре “Восьмерки” (Рисунок 4.7).
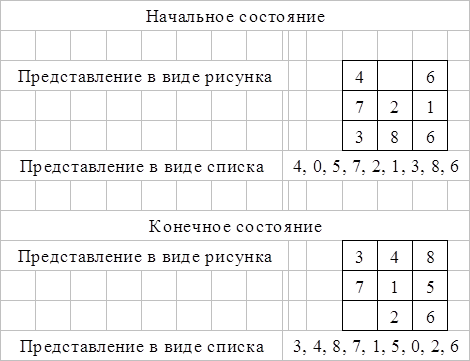
Рисунок 4.7 Задача «Восьмерки»
Предположим, что квадратные фишки с номерами перемещаются в квадратной рамке. Заданы начальное и конечное состояния. Задача заключается в нахождении последовательности перемещений фишек из начального положения в конечное. Любую фишку можно передвинуть по горизонтали или вертикали, если рядом есть свободное место, но двигаться по диагонали запрещено.
Количество состояний слишком велико для их непосредственного перебора. Вместо этого представьте программу, перемещающую фишки в определенном порядке от состояния к состоянию. Вычисляя эвристическую функцию для каждого состояния, она оценивает качество ходов. Такое исследование может быть выполнено несколькими способами с использованием эвристических функций.
Вместо слепого перемещения от одного состояния к другому нужно проранжировать все возможные ходы и выбрать тот, который сочтем лучшим. Обратимся к одной полезной эвристической функции, называемой расстоянием Хемминга. Это расстояние между данным состоянием и нулевым. В нашем случае оно измеряется числом фишек, находящихся не на своих местах (пустая позиция не засчитывается). Например, в следующей ситуации:
[4,0,5,7,2,1,3,8,6] положение в задаче
[3,4,8,7,1,5,0,2,6] положение цели
расстояние Хемминга равно семи. Если процедура поиска сможет найти положение, где расстояние Хемминга равно нулю, задача будет решена.
Одна из стратегий, заключается в том, что с помощью оценочной функции вы выбираете наилучший ход и проверяете тем же способом (используя оценочную функцию) все его следствия, прежде чем предпримете какие-либо другие шаги. В случае тупика нужно возвратиться к ближайшей развилке и попробовать сделать следующий наилучший ход. Эта стратегия известна как метод оврагов, который является вариантом процедуры поиска в глубину: сначала проверяются все следствия одного выбора на всю возможную глубину, и только потом происходит очередной выбор.
Метод оврагов, хотя и интересен, мало поможет при решении задачи "Восьмерка". Серьезный недостаток этой стратегии заключается в ее "близорукости" - для совершения выбора используется только локальная информация.
Существует другой вариант эвристического поиска, объединяющего в себе позитивные черты поиска в глубину и в ширину. Он известен под названием Лучший первый шаг, и в целом дает хорошие результаты. На каждой стадии поиска исследуется некоторое количество путей, и оценочная функция вычисляется для конечного состояния этих путей. В Лучшем первом шаге поиск продолжается от конечного достигнутого состояния, имеющего наилучшую оценочную функцию вверх до этого места. В этой стратегии часто происходят прыжки от конца одного пути к другому, пытаясь всегда работать с тем, что является наиболее обещающим. Для такого поиска требуется хранение большой информации, так как все частичные пути должны постоянно поддерживаться и большое время вычислений.
Есть еще одна оценочная функция, достаточно простая, но требующая значительно больше времени для вычислений. Она вычисляет для каждой фишки расстояние от ее исходного положения до конечного, а потом суммирует эти расстояния. Последние вычисляются по определенным правилам. Если фишка перемещается вдоль верхней рамки, то число шагов равно числу затрагиваемых фишек плюс один. В том случае, когда фишка перемещается от центра к периферии (или наоборот), число шагов равно единице, если она находится в примыкающей позиции, и равно двум, - если в диагональной позиции.
К сожалению, эвристический поиск может лишь ускорить решение задачи "Восьмерка". Нет поискового метода, быстро ведущего к прямому ответу. Это более сложная проблема, чем могло показаться вначале, во всяком случае, если применяется решение, основанное на поиске. Очевидно, люди решают такие задачи по-другому.
Существуют некоторые более "хитрые" стратегии, которые применительно к конкретным проблемным областям дают лучшие результаты, чем исследованные типы поиска. Обзор подобных стратегий дан в учебнике Elaine Rich, Artificial Intelligence, McGraw-Hill, New York, 1983.
Однако часто очень трудно, если не невозможно, найти такую функцию для многих задач реального мира. Одна из сложностей, о которой упоминалось выше применительно к шахматам, заключается в том, что в какой-либо из позиций игры, возможно, следует сделать ход, кажущийся менее удачным, с тем, чтобы позже достигнуть преимущества. Много усилий в работе, связанной с управляющими структурами в области искусственного интеллекта, было затрачено при попытках справиться с подобными сложными ситуациями. Две универсальные стратегии, примененные в экспертных системах, предлагают следующее:
а) организовать пространство задачи таким образом, чтобы в начале поиска решения можно было сказать, насколько оно будет успешным, в этом случае может быть исключена необходимость перебора всего множества путей поиска;
б) построить пространство задачи в виде ряда подпространств с минимальными взаимосвязями или без взаимосвязей между ними. В результате этого каждая из подзадач может быть решена независимо от решения последующих задач.
В следующей программе на языке Prolog определяется оптимальный маршрут по заданным критериям: по минимальному расходу бензина и по минимальному расстоянию.
Данные о расстояниях между пунктами находятся в файле pal.ddd в виде:
sosed("pc","a",1,100). sosed("a","b",1,120). sosed("b","c",2,400).
sosed("c","d",3,308). sosed("a","d",2,205). sosed("a","e",3,320).
sosed("e","h",3,290).
Предикат dcon проверяет, являются ли пункты соседними:
dcon(X,Y,M,N) :- sosed(X,Y,M,N);sosed(Y,X,M,N).
С помощью правила summa суммируем расстояние между текущими соседними пунктами и расход бензина:
summa([_],N,S,_,_) :- S=N.
summa([X,Y|L],N,S,Км,Бензин) :-
bound(Км),dcon(X,Y,M,_),
K=M+N, summa([Y|L],K,S,Км,Бензин);
bound(Бензин), dcon(X,Y,_,M), K=M+N, summa([Y|L],K,S,Км,Бензин).
Формируем списки со всеми возможними вариантами пути и используя правило min определяем путь с минимальным значением:
min([],Tmp,Cnt,_,Min,N) :- Min=Tmp, N=Cnt.
min([X|L],Tmp,Cnt,K,Min,N) :- Tmp>X, C=K, KK=K+1, MM=X,
min(L,MM,C,KK,Min,N);
KK=K+1, min(L,Tmp,Cnt,KK,Min,N).
Полный текст с интерфейсом пользователя приведен в Приложении 2.



