Процессы поиска на графе

Граф определяется как множество вершин вместе с множеством ребер, причем каждое ребро задается парой вершин. Если ребра направлены, то их также называют дугами. Дуги задаются упорядоченными парами. Такие графы называются направленными. Ребрам можно приписывать стоимости, имена или метки произвольного вида, в зависимости от конкретного приложения.

При формулировке задачи решение получается в результате применения операторов к описаниям состояний до тех пор, пока не будет получено выражение, описывающее состояние, которое соответствует достижению цели. Все методы перебора, которые мы будем обсуждать, могут быть смоделированы с помощью следующего теоретико - графового процесса:

Начальная вершина соответствует описанию начального состояния. Вершины, непосредственно следующие за данной, получаются в результате использования операторов, которые применимы к описанию состояния. Пусть Г- некоторый специальный оператор, который строит все вершины, непосредственно следующие за данной. Процесс применения оператора Г к вершине называется раскрытием вершины.

От каждой такой последующей вершины к породившей ее идут указатели. Эти указатели позволяют найти путь назад к начальной вершине, уже после того как обнаружена целевая вершина.

Для вершин, следующих за данной, делается проверка, не являются ли они целевыми вершинами. Если целевая вершина еще не найдена, то продолжается процесс раскрытия вершин (и установки указателей). Когда же целевая вершина найдена, эти указатели просматриваются в обратном направлении- от цели к началу, в результате чего выявляется путь решения. Тогда операторы над описаниями состояний, связанные с дугами этого пути, образуют решающую последовательность.

Этапы, указанные выше, описывают основные элементы процесса перебора. При полном описании процесса перебора нужно еще задать порядок, в котором следует раскрывать вершины. Если вершины раскрываются в том же порядке, в котором они порождаются, то получается процесс, который называется полным перебором,

Если же сначала раскрывается всегда та вершина, которая была построена самой последней, то получается процесс перебора в глубину. Возможно, однако, что имеется некоторая эвристическая информация о глобальном характере графа и общем расположении цели поиска. Такого рода информация часто может быть использована для того, чтобы “подтолкнуть” поиск в сторону цели, раскрывая в первую очередь наиболее перспективные вершины.

При поиске методом редукции решение задачи сводится к решению совокупности образующих ее подзадач. Этот процесс повторяется для каждой подзадачи до тех пор, пока каждая из полученного набора подзадач, образующих решение исходной задачи, не будет иметь очевидное решение. Подзадачи считается очевидной, если ее решение общеизвестно, или получено ранее. Процесс решения задачи разбиение на подзадачи можно представить в виде специального направленного графа G, называемого И/ИЛИ- графом. В графе выделяются два типа вершин: конъюнктивные вершины и дизъюнктивные вершины. Графическое представление вершин приведено далее на Рисунок 6.6.

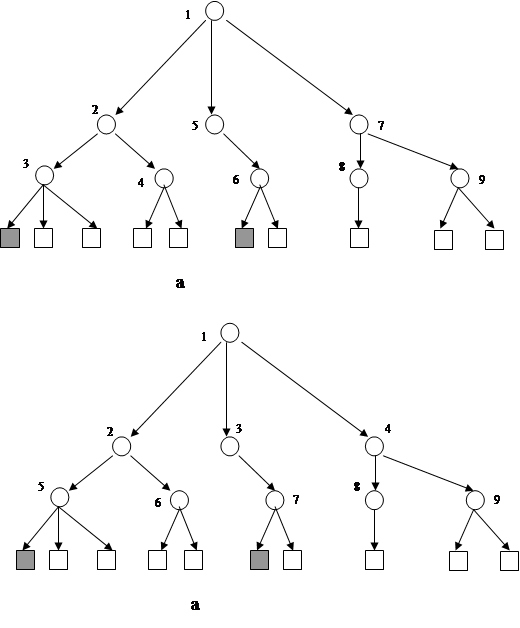
Рисунок 4.2 Пространство состояний, построенное поиском в глубину (а) и поиском в ширину (б)

Пример графического представления разбиения на подзадачи, приведен на Рисунок 4.3.

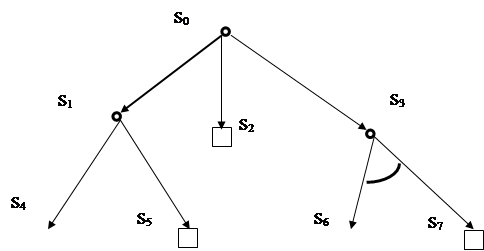
Рисунок 4.3 Графическое представление разбиения на подзадачи

Цель процесса поиска в И/ИЛИ графе- показать, что начальная вершина разрешима, т.е. для этой вершины существует решающий граф. Определение разрешимой вершины в И/ИЛИ графе можно сформулировать рекурсивно следующим образом:

1. Конечные (целевые) вершины разрешимы, так как их решение известно по исходному предположению.
2. Вершина ИЛИ разрешима тогда, и только тогда, когда разрешима по крайней мере одна из ее дочерних вершин.
3. Вершина И разрешима тогда и только тогда, когда разрешима каждая из ее вершин.

Решающий граф определяется как подграф из разрешимых вершин, каждый показывает, что начальная вершина разрешима.

Следующая программа иллюстрирует стратегию поиска в глубину и обратную цепочку рассуждений. Предположим, дерево (Рисунок 4.4) отражает транспортное сообщение между населенными пунктами.

Факты, означающие прямую связь между узлами графа (городами), могут выглядеть так:

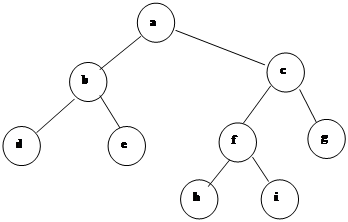
Рисунок 4.4 Транспортное сообщение между населенными пунктами

Добавим косвенную связь connect(X,Y) для исключения зацикливания.

Правило на языке PROLOG, определяющее маршрут вниз по дереву, выглядит так:

connect(X,Y) if dconnect(X,Y).

Факт connect(X,Y)- истинна, если истина факт dconnect(X,Y).

Правило, проверяющее, есть ли связь между пунктами X и Y через промежуточный пункт Z:

connect(X,Y) if dconnect(X,Z), dconnect(Z,Y).

Простое правило всегда ставят первым - это уменьшит время поиска решения. Стратегию поиска в глубину применяют для решения проблемы, где все пути поиска от вершины дерева до его основания имеют одинаковую длину. При неодинаковой длине пригоден поиск в ширину. Текст программы, проверяющей есть ли связь между пунктами X и Y приведена в Приложении 1.

Приведенная в предыдущей главе управляющая структура относится к одной из простых; она сводится к перебору правил, пока одно из них не выполнится, и повторению цикла с самого начала. В большинстве реальных систем задача управления значительно сложнее.